Basics
Triangles
Lines
Parallel Line Relationships
Congruence Theorems
100
If a, b, and c are real numbers and a = b,
then a + c = b + c.
Addition Property
of Equality
100
Triangles add up to 180 degrees
Triangle Sum Theorem
100
Two lines that never touch
Parallel Lines
100
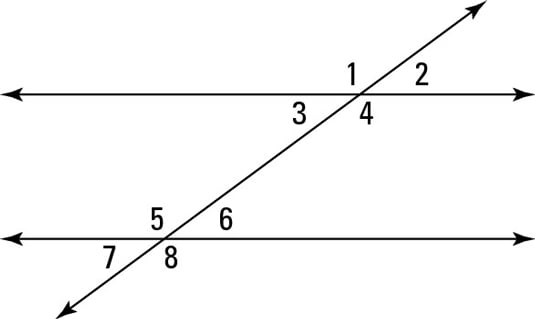
Angles 1 and 5 relationship
Corresponding Angles
100
When all corresponding sides are congruent
Side-Side-Side
200
If a, b, and c are real numbers and a = b,
then a - c = b - c.
Subtraction Property
of Equality
200
A triangle with two congruent sides and two congruent angles
Isosceles Triangle
200
Name of the line that cuts through at least two other lines
Transversal
200
Angle 3 and 6 relationship
Alternate Interior Angles
200
When a corresponding angle is between two corresponding sides
Side-Angle-Side
300
If a is a real number, then a = a.
Reflexive Property
300
Type of triangle with equal sides
Equilateral Triangle
300
Angles formed from two intersecting lines, are congruent
Vertical Angles
300
Angle 2 and 7 relationship
Alternate Exterior Angles
300
When a corresponding side is between two corresponding angles
Angle-Side-Angle
400
If a and b are real numbers and a = b, then a can be substituted for b.
Substitution Property
400
Type of Triangle with a 90 degree angle
Right Triangle
400
Lines which form 90 degree angles when they intersect
Perpendicular Lines
400
Angle 3 and 5 relationship
Consecutive (same side) Interior Angles
400
When two corresponding Consecutive Angles are followed by a corresponding Side
Angle-Angle-Side
500
If a, b, and c are real numbers, a = b, and b = c, then a = c.
Transitive Property
500
Look on board, What theorem proves Angle 4 is 100 degrees
Triangle Exterior Angle Theorem
500
When a line/line segment is split into equal parts, it has been...
bisected
500
Angle 1 and 6 relationship
None
500
Right Triangle Specific Congruence Theorem
Hypotenuse-Leg