What is the difference between Arithmetic and Geometric Sequences?
Arithmetic has common difference and Geometric has common ratio.
Arithmetic uses addition/subtraction and Geometric uses multiplication/division.
If f(x)=a(1+r)x
Then what is the initial amount and growth rate?
initial amount=a
growth rate = r
If f(x)=a(1-r)x
Then what is the initial amount and decay rate?
initial amount = a
decay rate = r
When interest is compounded quarterly, what do we use as n?
n= 4
Keeping your answer in positive exponents, simplify:
y^(3) * 7y^3
What is
7y^6
Is the sequence below arithmetic or geometric? Explain your answer.
200, 100, 50, 25, 12.5, 6.25
Geometric with a common ratio of 1/2
In exponential functions when b>1 this will cause an exponential growth or decay?
Exponential growth
In exponential functions when 0<b<1 this will cause an exponential growth or decay?
Exponential decay
How do you turn 7% into a decimal?
What is the given decimal of 7%?
7/100= .07
or you move the decimal two places to the left of 7 to get .07.
Keeping your answer in positive exponents, simplify:
4p^-3
What is
(4)/(p^3)
Write a formula for the following geometric series:
2,10,50,250,...
an=2(5)n
Does the graph represent exponential growth or decay?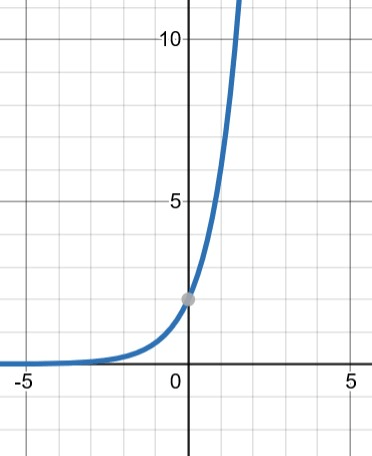
Exponential Growth
Does the graph represent exponential growth or decay?
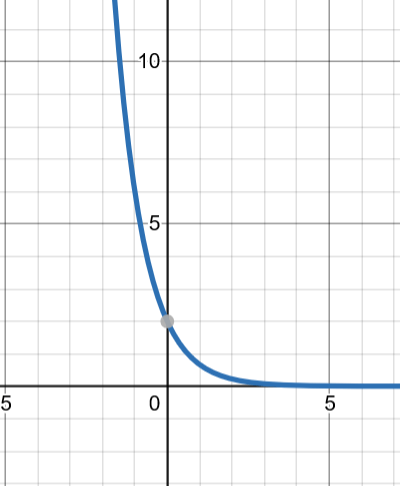
Exponential Decay
Ms. Wiggins deposited $1,000 in a CD at a 7% interest compounded quarterly. How much will her CD be worth in 5 years?
Identify the P,r,n & t.
p=1,000
r=.07
n=4
t=5
Keeping your answer in positive exponents, simplify:
(x^(2)y^(5))^2
What is
x^(4)y^(10)
Write a formula for the geometric sequence below:
5,-10,20,-40,80,...
An=5(-2)n-1
What equation would represent the situation below?
Gina started with 14 frogs in 2004. Her frogs increase at a rate of 20% each year. How much frogs would she have in 2008?
y=14(1+0.2)4
What is the equation we can use to represent the situation below?
Marvin invested $1000 a stock that is going down each year by 0.5%. In 5 years, how much money would he have left?
y=1000(1-0.005)5
$950 at 6.5% for 8 years compounded annually. What is the exponential model (equation, not answer) that represents exponential growth?
A=P(1+r/n)nt
A=950(1+.065/1)1(8)
Keeping your answer in positive exponents, simplify:
(-8mn^4)/(-7mn)
What is
8/(7n^3)
Find A7 (the seventh term) in the sequence below.
1000, 100, 10, 1,...
An=1000(1/10)n-1
A7=1000(1/10)7-1=1000(1/10)6= 0.001
Annual sales of a fast food restaurant are $530,000 and increasing at a rate of 5%. What will the annual sales be in 6 years?
A=P(1+r)n
530000(1.05)6
=$710,250 or =$710,251
Ms. Wiggins purchased a car for 26,400 and every year it depreciates by 12%. What she expect the value of her car to be after 3.5 years?
A=P(1-r)n
f(x)=26400(.88)3.5
=$16,876 or =$16,877
$1500 at 5% interest rate compounded monthly. What will be the balance after 2 years?
=$1,657
Keeping your answer in positive exponents, simplify:
(3x^3)/y^-6
What is
3x^(3)y^(6)