If, y=a(b)x, What do a and b represent?
a=initial amount/y-intercept
b=(common ratio)(growth or decay factor)
y=2(0.93)x
How do you know if this function represent exponential growth or decay?
Exponential Decay
The b value is between 0 and 1.
The function y = 12(3)x models an insect population after x weeks.
What will the population be after six weeks?
8,748 insects
In exponential functions, when b>1 this will cause an exponential growth or decay?
Exponential growth
A Petri dish contains 50 bacteria. The number of bacteria doubles every day.
a) What is the initial amount?
b) What is the growth factor?
c) Write the exponential equation that represents this scenario.
d) Now find the number of bacteria in the dish after 2 weeks.
a) 50
b) 2
c) y= 50(2)x
d) y= 50(2)14
819,200 bacteria
y = 45(1.07)x
Give the RATE as a % for this exponential function
Growth or Decay?
Exponential Growth. 7%.
Which number is the y-intercept and which is the growth factor for the function y=2(3)x
y-intercept=2
growth factor= 3
Do the following equations represent exponential growth, decay, or neither?
a) y=3.5(0.3)x
b) y=2(3)x
c) y=5x+6
a) Decay
b) Growth
c) Neither (It's linear! y=mx+b)
Write the exponential equation:
Initial Amount= 550
Decay FACTOR = 0.67
y=550(0.67)x
Does the graph represent exponential growth or decay?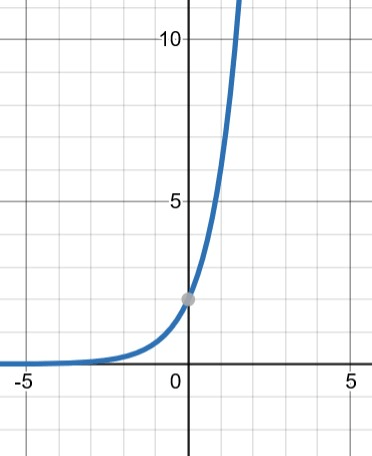
Exponential Growth
You purchased a new computer for $1500. It decreases in value by about –18% each year. How much will your computer be worth in 6 years?
About $456
What is the RATE of growth or decay in the following expression?
y = 1400(0.92)5
8% decay
Name the y-intercept and write the equation for the graph below?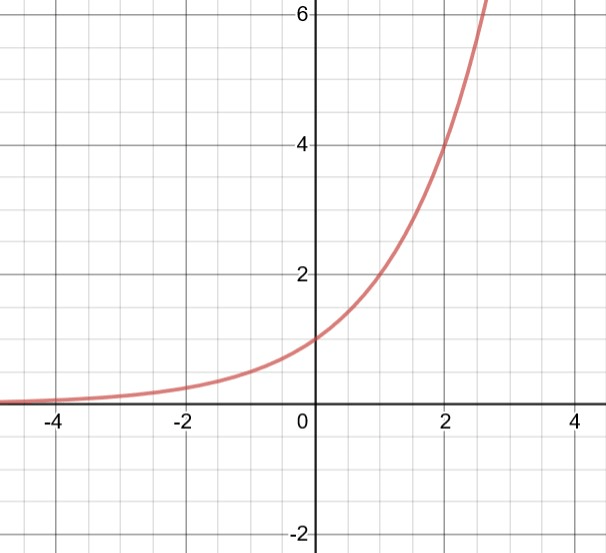
y-intercept: 1
growth factor: 2
y= 1(2)x
Is the function exponential growth or decay? What is the b-value? Write the equation. 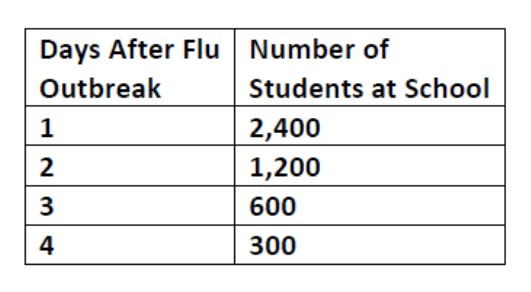
Decay
b=1/2
y=4,800(1/2)x
y= 2,300 (0.98)x
If this equation models enrollment at Cary High after 2020. What will the school enrollment be in 2030?
1879 students
What's the growth factor? (the b value in equation)
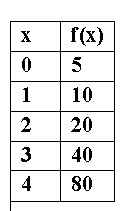
b=2
The population of a town is 18,000 and is decreasing at a rate of 2% per year. What is the population after 3 years?
y= 18,000(0.98)3
16,941 people
What is the rate (the % increase or decrease) given the equation
y = 100 ∙ (0.75)x
A. 25% B. 75% C. 100% D. 175%
25% decrease
1 - .75 = .25
Arithmetic sequences are modeled by __________ functions.
Geometric sequences are modeled by ___________ functions.
linear
exponential
y = 4(0.7)x
What is the decay factor?
What is the decay rate?
0.7 decay FACTOR
30% decay RATE
Given equation: y = 80(1/2)x
Fill in the table:
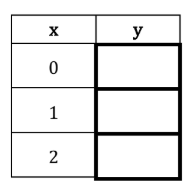
(x, y)
(0, 80)
(1, 40)
(2, 20)
A colony of bacteria grows by 35% every hour. If the colony began with 100 bacteria, how many are there after 12 hours?
y= 100(1.35)12
3664.42 bacteria
The population of rabbits doubles every 6 months. If there are initially 100 rabbits, how many will there be after 2 years?
y=100(2)4 = 1600 rabbits
y= 5(1.97)x
a. Does this function represent exponential growth or decay?
b. What is the growth/decay RATE
Exponential Growth
Rate: 0.97 or 97%
All of the following indicate exponential decay EXCEPT which term?
decrease
depreciate
deposit
decay
deposit
y = 115 (0.42)x
Initial Amount= _____
Growth or Decay FACTOR = ______
Growth or Decay RATE = _____
Initial Amount= 115
Growth or Decay FACTOR = 0.42
Growth or Decay RATE = 58%
Write the equation given the initial amount and the decay rate.
Initial: 230
40% decay
y = 230 (0.60)x
Annual sales of a fast food restaurant are $530,000 and increasing at a rate of 5% per year. What will the annual sales be in 6 years? (show the equation and answer)
y= 530,000 (1.05)x
$710,250.69 in annual sales.
The cost of tuition at a college is $12,000 and is increasing at a rate of 6% per year
What will be the cost in 17 years?
$32,313.27
Identify the initial amount, the growth factor and the percent growth rate. y = 12(1.23)x
initial amount: 12
growth factor: 1.23
rate: 23% growth