Graphs
Growth vs Decay
Negative Exponents
Equations
100
Does this graph show Exponential Growth, Exponential Decay, or Neither?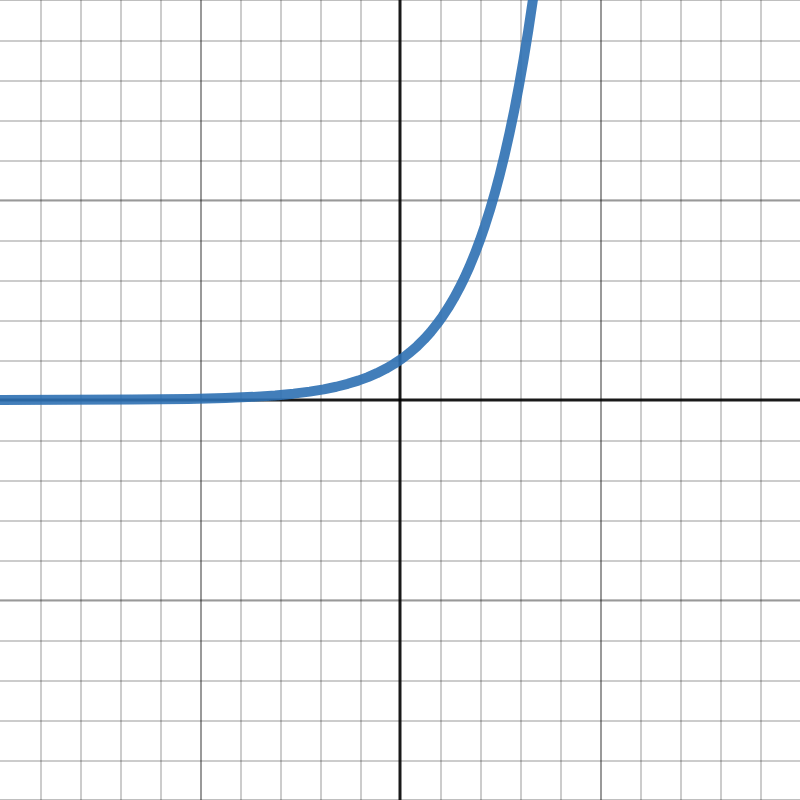
Exponential Growth
100
State whether this is exponential growth or decay and why: y=5*(1/2)^x
Exponential Decay: growth factor is 1/2 , which is between 0 and 1
100
What is the value of
4^-2 ?
1/16
100
A population of bacteria in a petri dish is modeled by the equation y=5^t*900 . What is the initial population?
900
200
Does this graph show Exponential Growth, Exponential Decay, or Neither?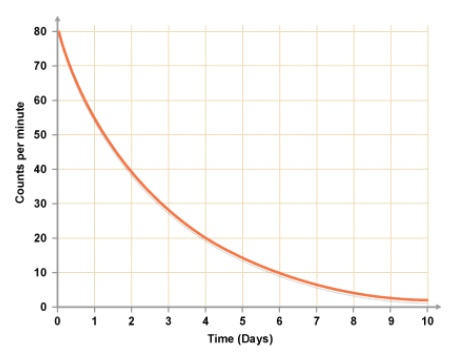
Exponential Decay
200
State whether this is exponential growth or decay and why:
y=2*(6/5)^x
Exponential Growth: Growth factor is 6/5 , which is greater than 1
200
The population of pandas in an area of the forest is demonstrated by the following equation: p=600*(2)^t . What is the population when t=-3?
75 pandas :)
200
A population of bacteria in a petri dish is modeled by the equation y=1600*(1/6)^t . What is the growth factor?
1/6
300
What is the initial value of this graph?
1
300
State whether this is exponential growth or decay and why:
y=(1/4)*(10/7)^x
Exponential Growth: Growth factor is 10/7 , which is greater than 1
300
Find (4/3)^-3
27/64
300
Michael invests $400 in Gamestop. The investment doubles each year. Write the equation that represents this situation, where y represents the value of the investment and t represents the time in years.
y=400*2^t
400
What is the growth factor for this exponential function?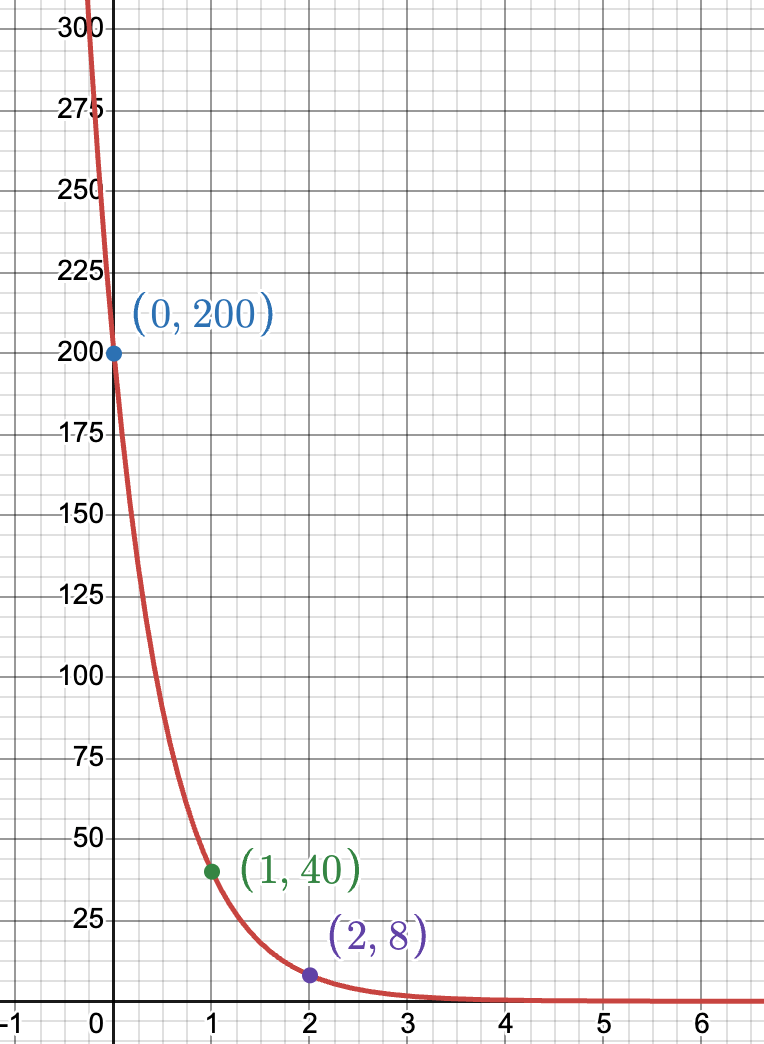
1/5
400
State whether this is exponential growth or decay and why:
y=14^x*(8/9)
Exponential growth: Growth factor is 14, which is greater than 1
400
A population of salmon is measured by scientists every year and is represented by the equation p=2000*(4)^t . Give a full description of what it means for the situation when t=-1.
1 year before scientists measured the population of salmon, there were 500 salmon.
400
A car loses 1/4 of its value each year. What is the growth factor in its equation?
3/4
500
A small town's population is demonstrated by the following equation: p=9000*(3)^t . What is the value of t when the population is 1000?
t=-2
500
A car loses 5/12 of its value each year. It started at $5000. What is the equation that represents this situation?
y=5000(7/12)^x