What type of exponential function is it?
Modeling Scenarios
Applying Exponential Functions
Transformations
Extend your thinking
100
17, 51, 153, 459, ...
Geometric sequence
100
Cyril's new Tesla truck was $68,500 when he first bought it. It immediately lost $12,000 of value when he drove it off of the lot. If it continued to decrease in value by 15% each year he owned it, what would it be worth in 6 years when he has paid it off?
y=56500(0.85)^6
100
The equation f(x) = 422,000(1.12)x represents the population of a city every year. In 15 years, what will the population of the town be?
What is about 2,309,844
f(x) = 422,000(1.12)15
100
Describe the transformation in the following function:
f(x) = 2x
g(x) = 2x +5
Translated up 5 units
100
what does the n stand for in the compounding interest formula?
number of times compounded per year
200
Jimmy puts all of his earnings from working at the summer camp into a college fund account that will give a 7% return, bi-annually for 10 years.
Compounding interest
200
Amelia invests $1,200 in a top end hamster cage which increases in value by 20% annually. How might she know the value of her hamster cage at any point in time?
f(x)=1,200(1.2)x
200
The following equation represents the amount of Elephants over the course of a number of years:
f(x) = 20,000(0.85)x
If they started taking the data in 2010, how many elephants will there be in 2020?
What is about 3,937
f(x) = 20,000(0.85)10
200
Describe the transformation in the following function:
f(x) = ex
g(x) = e(x+4)
Translated four units to the left
200
Suppose that you have $6344.93 in a saving account after 4 years. If the rate of 6% and it compounded quarterly. Find the initial amount your parents deposited for you.
P= 5000
300
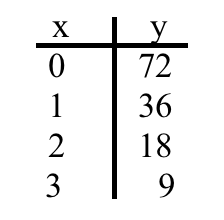
Decay
300
Mr. Smith decides he wants to grow a Santa beard. The internets says that the average beard grow three tenths of a millimeter per day. If his beard is already twenty five millimeters, how might he determine how long his beard will be in a month or a year or a decade?
y=.3x + 25
300
A bunny family totaled 154 in 2018. The family grew at an annual rate of 1.032. How large will the family be 2025?
What is about 192
f(x) = 154(1.032)7
300
Describe the transformation in the following function:
f(x) = (1/2)x
g(x)= (1/2)x-2 +4
2 units to the right and 4 units up
300
What type of function out of the four types we deal with this year is the most similar to exponential functions? Explain how they are different.
Linear is repeated addition...exponential is repeated multiplication
400
An electrical store calculates that the number of DVD players sold is 87% of what was sold the previous year.
Decay
400
The half-life of Po-214 is .001 seconds. How much of a 10mg sample is left after .003 seconds?
10(1/2)^.003/.001 or 3
400
The fish in Lake Washington were declining at an annual rate at 1.5%. Their current number is estimated at 2500. How many fish will there be 20 years from now?
What is about 1,847 fish
y = 2500(.985)20
400
Describe the transformations from the red function(y=3^x) that took place by writing the equation for the blue line?
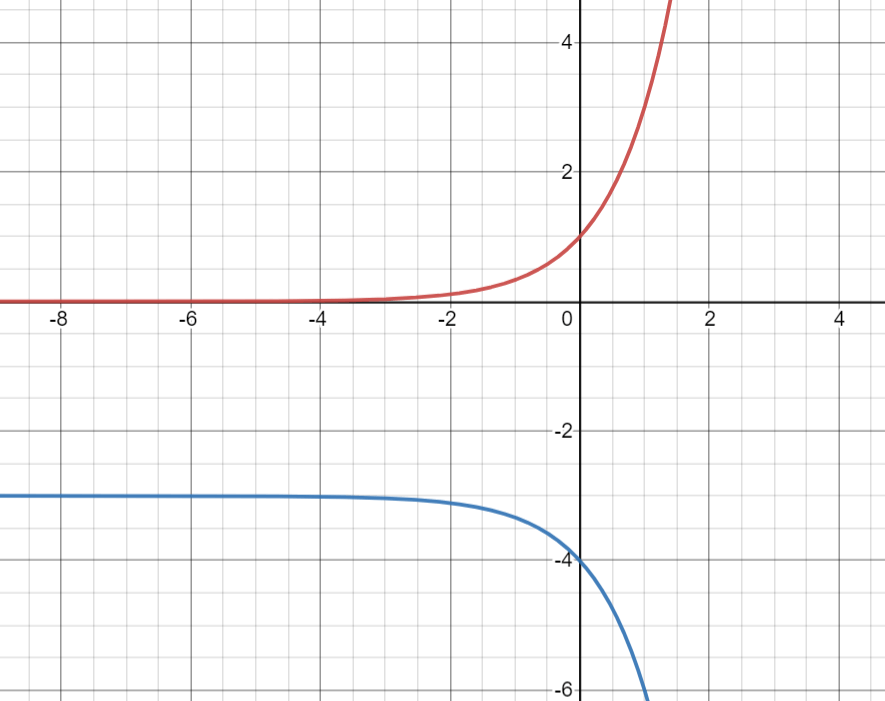
Reflected over the x-axis, translated down 4 units
y= -3x -3
400
What are the two "most important" points when working with exponential functions?
x=0 and x=1
500
An isotope has a half life of 6 hours. How much of the isotope will be present in 24 hours?
Decay
500
Lamar purchases Takis stock at the value of $20 a share. The next day, that stock was down to $8 a share, and on the following day it was only worth $3.20.
y=20(0.4)x-1
500
Serena bought a laptop 4 years ago, but she doesn't remember how much it cost. But right now, she knows it's worth $1,024. She knows it decreases in value by 20%.
How much did she buy it for?
What is $2500
1,024=b(0.8)4
500
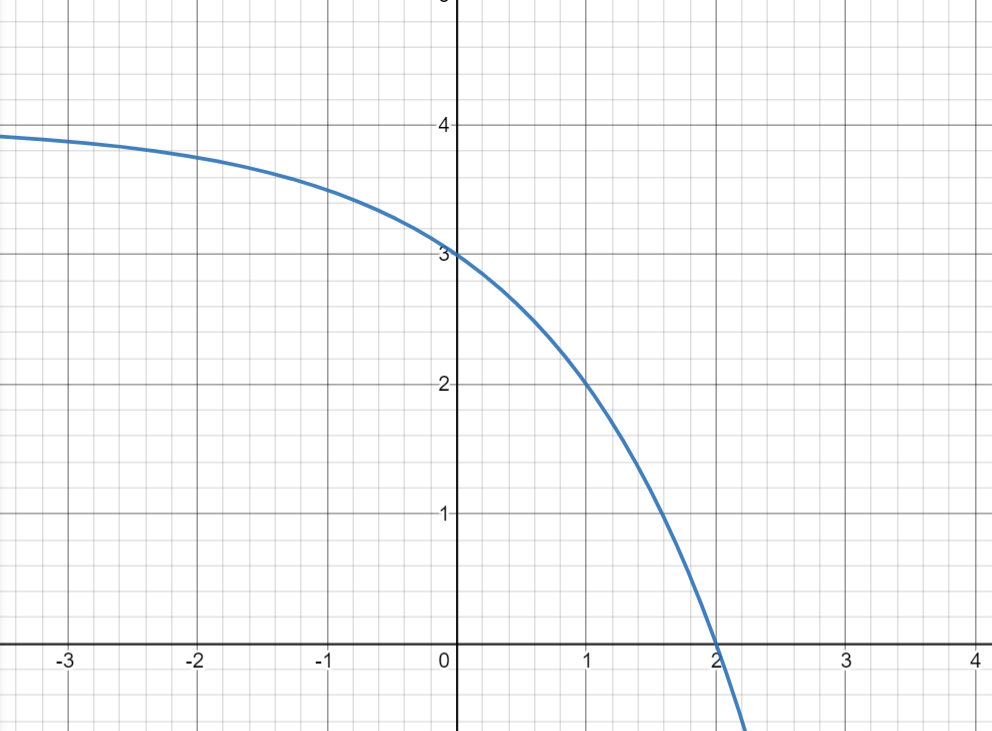
Draw the graph of 2^x after a reflection and and vertical slide of plus 4.
500
solve for x:
52x = 21
log5(21)=2x so...
x=[log5(21)]/2
or
x=.9458340748