A rumor is spreading and originally only 3 people knew the rumor. Every day, the number of people who knows doubles.
How many people will know in a week?
384 people
Consider the exponential function: f(x) = 3(12)x
What is the constant ratio?
b =12.
A function has a constant ratio(b-value) of 3.
Is this growth or decay?
growth - because 3 is greater than 1.
What's the y-intercept?
y-intercept: (0,5)
In 2010, your favorite snack cost $4. With inflation, the price is increasing by % 2each year.
Write a function to represent this scenario.
f(x) = 4(1+0.02)x or f(x) = 4(1.02)x
A function is increasing by 45%. What is the constant ratio (b-value)?
b = 1 + 0.45
b = 1.45
You are bidding on an item at an auction. At 3pm, the price was $50. It seems to be increasing its price by 25% every hour.
How much will it be bidding for by 8pm?
$152.59
Consider the exponential function: f(x) = 10(0.5)x
What is the y-intercept?
The y-intercept is (0, 10)
A function has a constant ratio(b-value) of 0.3.
Is this growth or decay?
Decay - because 0.3 is less than 1.
What's the constant ratio?

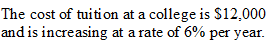
Write an exponential function for this scenario.
f(x) = 12,000(1+0.06)x
or f(x) = 12,000(1.06)x
A function is decreasing by 20%. What is the constant ratio (b-value)?
b = 1 - 0.2
b = 0.8
3224
What is the difference between a linear function and an exponential function?
Linear functions have constant change (adding the same amount).
Exponential functions don't have constant change, but they do have a constant ratio (multiplier).
f(x)=25(1.07)x
Does this function represent exponential growth or decay?
Exponential Growth.
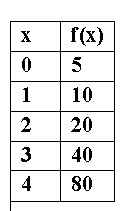
Write the exponential function represented by this table. (Round the constant ratio)
f(x) = 5,005(1.2)x
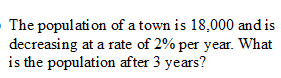
Write the function AND answer the question.
Function: f(x) = 18,000(1 - 0.02)x
or f(x) = 18,000(0.98)x
After 3 years the population will be: 16,941 people
A function is increasing by 2%. What is the constant ratio (b-value)?
b = 1 + 0.02
b = 1.02
Antibiotics work to kill bacteria inside your body. It decreases the bacterial load by 10% every hour. If your initial viral load was 5,000, how many full hours will it take for your viral load to be under 500?
22 hours
or ~21.85 hours
Decay functions have a constant ratio that is between _____ and ____
It is between 0 and 1
f(x)=1300(0.98)x
Does this function represent exponential growth or decay?
Exponential Decay
Write the exponential function represented by this table.
f(x) = 2100(1.03)x
You put $500.00 into an account and the account earns 4% interest, compounded annually (each year). How much will be in the account after 5 years?
Write the function AND answer the question.
Function: f(x) = 500(1 + 0.04)x
or f(x) = 500(1.04)x
After 5 years, the account will have: $608.33
A zombie outbreak is modeled by the function where x measures the number of days:
f(x) = 4(1.15)x.
1) How many zombies started the outbreak?
2) How many zombies will there after a week (7 days)?
1) 4 zombies started the outbreak
2) There will be 10 zombies after 7 days.
The population of fox decrease as the bunny population also decreases. The fox are decreasing by 35% each year. If the population started at 8000 this year, approximately how many fox will exist in 2027?
2197 fox
Growth functions have a b value that is ______ than 0
greater
f(x)=25(1)x
Does this function represent exponential growth or decay?
Neither!
Write the exponential function represented by this table.

f(x) = 20(0.5)x
Your car cost $42,500 when you purchased it in 2015. The value of the car decreases by 15% annually (each year)
What is the value of your car now?
f(x) = 42,500(1 - 0.15)x or
f(x) = 42,500(0.85)x
Your car's value now (8 years later) is: $11,580.85
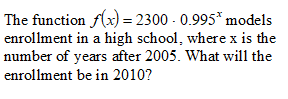
2243