GCF
Difference of squares and perfect squares
Trinomials
Solve
Graphs
100
6x^2+18x-12
6 (x^2 + 3 x - 2)
100
64-p^2
(64+p)(64-p)
100
x^2+2x-24
(x-4)(x+6)
100
(x+6)^2-16=0
x=-10,-2
100
True or False. Every y-value of the graph of a quadratic function has two different x-values.
True
200
15abc^2+25a^3bc
5 a b c (3 c + 5 a^2)
200
49m^4-100n^2
(7m^2+10n)(7m^2-10n)
200
x^2 - 15 x - 100
(x + 5) (x - 20)
200
x^2-6x+9=0
x=3
200
True or false. It is possible for the graphs of two different quadratic functions to each have x=-3 as its line of symmetry and both have a maximum at y=5?
True
300
8m^2p^4-24m^3p^5
8m^2p^4(1-3mp)
300
x^2+18x+81
(x+9)^2
300
2x^2-18x+36
2(x-6)(x-3)
300
x^2 + 7 x - 170 = 0
x=-17, 10
300
Leading coefficient positive or negative?
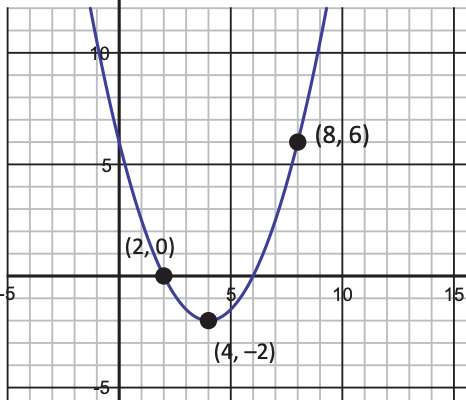
Positive
400
10xy^3-25x^2y^3+15x^3y
5xy(2y^2-5xy^2+3x^2)
400
9x^2-16
3x-4
400
8x^2-18x-5
(4x+1)(2x-5)
400
5x^2-20x+15=0
x=1, 3
400
Vertex and axis of symmetry
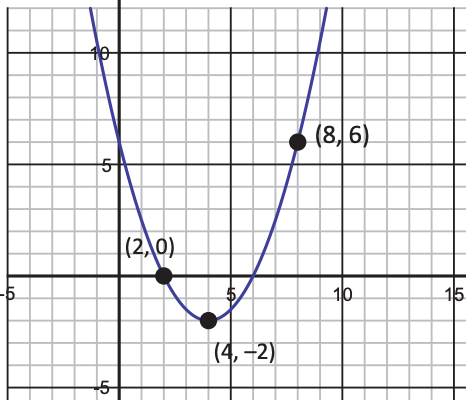
Vertex: (4, -2)
Axis of symmetry: x = 4
500
49s^2t^2-36s^2t^2
13 s^2 t^2
500
x^2-26x+169
(x-13)^2
500
-2x^2-7x-3
-(x+3)(2x+1)
500
3x^2+14x-5=0
x=-5, 1/3
500
f(0) and f(6)
f(0)=6
f(6)=0