The height in meters, h, of a model rocket above the ground is given t seconds after launch by the equation:
h(t) = -5t^2 +40 t
What is
h(10)?
h(10) = -100
Which of the following is a coterminal angle of
theta = (5pi)/9 ?
a. theta = (25pi)/9
b. theta = -(23pi)/9
c. theta = (23pi)/9
d. None of These
c. theta = (23pi)/9
What is the reference number of the value
t = (5pi)/6 on the unit circle?
\overlinet =pi/6
Find the amplitude of the graph of the function:
y = -4-1/3cos(x+pi/3)
Amplitude = 1/3
Complete the number crunch:
102->divide 2-> 2/3 of this
-> +6 -> divide 5
8
The flight of a certain bird is modeled in the graph shown. What is the range of the bird's flight?
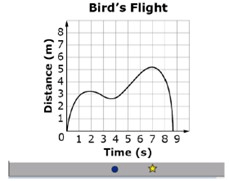
0<=y<=5.1
Find a positive coterminal angle to
theta=-(17pi)/4 in radians
theta=(7pi)/4
A number t lies on the unit circle
in quadrant II. Determine the sign that makes the statement true:
sin (t) ? cos (t)
<, >, =
sin (t) > cos (t)
Describe the transformation of the function from its parent graph:
y = 2-sin(x-pi/6)
2 units up, Flipped across x-axis
pi/6 to the right
Complete the Algebra Crunch:
3x -> squared -> -16 -> factor it -> divide (3x-4)
-> (3x+4)
A function f(x) has the following attributes:
-5<=x<=15
0<=f(x)<=45
Which of the following statements MUST be false?
a. f(0)=0
b. f(-15) = -20
c. f(5) = 40
f(9)=45
b. f(-15) = -20
Convert the angle into radians in terms of pi and in simplest form
theta = 700^o
theta = (35pi)/9 radians
Find the missing coordinate point of P using the fact that P lies on the unit circle in the given quadrant:
P( x , 2/3) in Quadrant II
x = -sqrt5/3
Find the y- intercept of the graph of the function:
y = -1-sin(x)
(0,-1)
How many FULL revolutions will an angle of 40 radians make around the unit circle?
6 Full Revolutions
Consider a sequence whose first five terms are
6, 12, 24, 48, 96
Determine the function, with domain {1,2,3,4,5} , that defines this sequence
S_n=6(2)^(n-1)
Determine how many radians the hour hand of an analog clock moves through 5 hours.
5pi/6 radians
Find the terminal point of t = -(35pi)/4
on the unit circle
(-sqrt2/2, -sqrt2/2)
The coordinate point (pi,0) lies on the graph of a
parent trigonometric function
y = sin x determine the new coordinate point for the
transformed function: y = -2+sin(x-(2pi)/3)
((5pi)/3, -2)
Find the EXACT value of the expression:
sec ((11pi)/3)
2
During the first years of growth the height of a tree can be modeled with the function
h(t)=-t^2+12t+10
where t is the time in years since being planted and h is the height in inches. Find the average rate of change, in inches per year, from year 1 to year 8.
3 inches per year
Evaluate the EXACT value of the expression:
-tan((3pi)/4)+2cos(2pi)-4sin((7pi)/6)
5
In a right triangle,
sin(A) = cos (B)
What is
A+B ?
A+B=90^o
Find the equation of the graph of the transformed function shown:
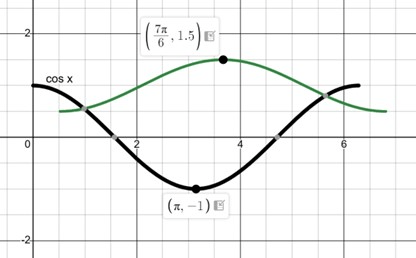
y = 1-1/2cos(x-pi/6)
Mary returned home in 2.5 hours walking at a constant speed of 3 miles per hour. Her distance from home can be modeled as a function of time. What coordinate point represents Mary's starting point?
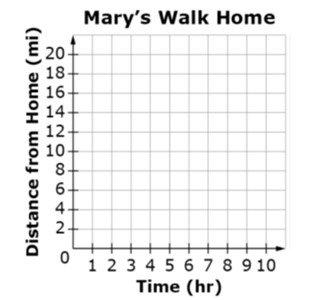
(0, 7.5)