Simplifying & Linear Equations
Slope, Graphs & Functions
Quadratics
Radicals & Rational Expressions
Composition, Domain & Inverses
Exponents & Logarithms
100
Simplify.
8x-(2x-14)
6x + 14
100
Determine whether the graph is the graph of a function.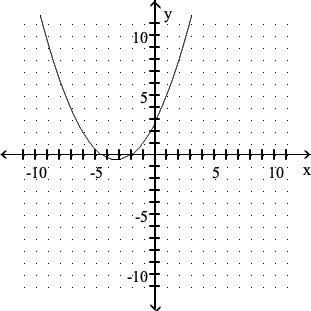
Yes, Function
100
Factor.
x^2 + 6x - 16
(x + 8)(x - 2)
100
Simplify by factoring.
sqrt75
5sqrt3
100
Find the inverse of the relation.
{(-19, -7), (2, -7), (9, 7)}
{(-7, -19), (-7, 2), (7, 9)}
100
Simplify.
(x^-3y^6)^-3
x^9/y^18
200
Solve.
-2b - 1 = 3 + 3b
b=-4/5
200
Graph using the slope and the y-intercept.
y = 1/2 x - 4
200
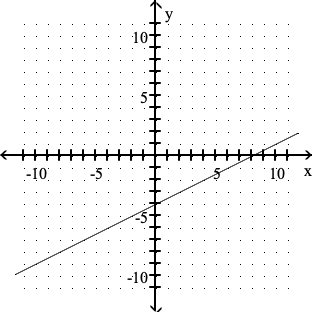
Solve the equation by factoring.
x^2 - x = 30
x= -5, 6
200
Rationalize the denominator.
sqrt(25/6)
(5sqrt6)/6
200
Find the domain. Write interval notation for the answer.
f(x) = (x^2 + 1) / (x - 4)
(-∞, 4) ∪ (4, ∞)
200
Rewrite without rational exponents, and simplify, if possible.
x^(1/5)
squareroot5 (x)
300
Solve.
|8x - 9| = 4
{5/8, 13/8}
300
Find the slope of the line containing the two given points.
(5, -17) and (11, -4)
13/6
300
Use the quadratic formula to find the exact solutions.
x^2 - 14x + 58 = 0
x= 7 ± 3i
300
Write an equation for a function that has a graph with the given characteristics.
The shape of sqrt(x) is shifted 6 units to the left. Then the graph is shifted 3 units upward.
f(x)=sqrt(x+6)+3
300
Determine the intervals on which the function is increasing, decreasing, and constant.
Increasing on (-2, 0) and (3, 5)
Decreasing on (1, 3)
Constant on (-5, -2)
300
Convert to an exponential equation.
ln 51 = 3.9318
e^(3.9318) = 51
400
Multiply.
(2x + 10)(x + 7)
2x^2 + 24x + 70
400
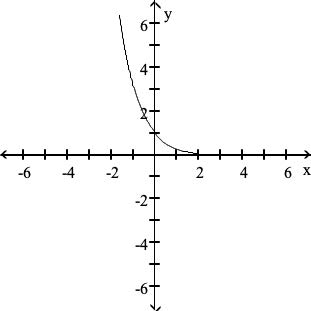
Graph the function.
f(x) = (1/3)^x
400
Use the graph to find the vertex, the axis of symmetry, and the maximum or minimum value of the function.
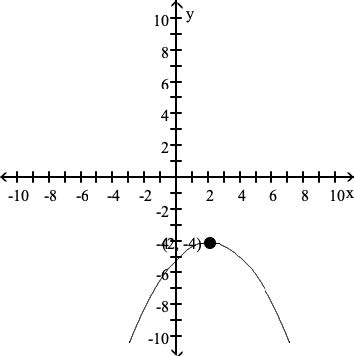
(2, -4); x = 2; maximum: -4
400
Solve:
sqrt(2x-3)-3=0
x=6
400
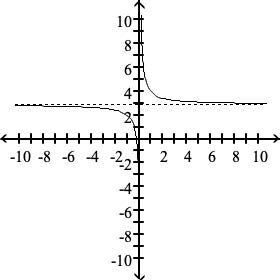
Graph the function, showing all asymptotes (those that do not correspond to an axis) as dashed lines. List the x- and y-intercepts.
f(x) = (3x + 1)/( x)
x-intercept: (-1/3 , 0)
no y-intercepts
400
Solve the exponential equation.
5^(9 - 3x) = 125
x=2
500
For the pair of functions, find the indicated sum, difference, product, or quotient.
f(x) = 5x - 5 , g(x) = 8x - 2
Find (f - g)(x).
-3x - 3
500
Find an equation of the line having the specified slope and containing the indicated point. Write your answer in slope-intercept form.
m = -3 ; (-9, 6)
y = -3x - 21
500
Solve.
A projectile is thrown upward so that its distance above the ground after t seconds is h(t) = -16t^2 + 312t. After how many seconds does it reach its maximum height?
10 seconds
500
Find the requested function value.
f(x) =-2x - 9 g(x)=-3x^2 - 8x + 1
Find (f ∘ g)(6).
301
500
For the piecewise function, find the specified function value.
f(x) ={ 5x, for x ≤ -1,
{x - 5, for x > -1
Find f(-2).
-10
500
Express in terms of sums and differences of logarithms.
loga x^2yz^4
2logax+logay+4logaz