The slope and y-intercept of y = -1/2x + 1
What is -1/2 and 1?
Whether (-3, 3) is a solution to -x + 3y > 10
What is yes?
The degree of -2x2yz3
What is 6?
x2 - 100 in factored form
What is (x - 10)(x + 10)?
The simplified form of √ 96
What is 4√ 6?
The x- and y-intercepts of 4x - 12y = 12
What is 3 and -1?
The inequality represented by the following graph:
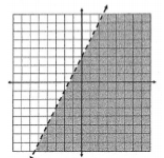
What is y < 2x + 3?
The product of (x + 4)2
What is x2 + 8x + 16?
The first step to factoring:
4x2 - 10xy + 24y2
What is GCF?
The conjugate of 3 + 2√ 2
What is 3 - 2√ 2?
The equation of this line in point-slope form
<img data-fr-image-pasted="true" src="data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAARcAAAECCAYAAADUyJP8AAAgAElEQVR4Aezd2bNk2XUe9pWZd665ekJ39YC5MRBAAyCIJkACFGAOUsiWbJNBP5DhV9kP+l8UHl7ECD+IokyHbYlB0hJBgiABEiAGNkCBmMEGGw303NXVVXXrDjk5fufer2r34b15qwoXNh5qRezc01rfmvbZ52TmOZmD+Xw+rzt0JwJ3InAnAsccgeEx492BuxOBOxG4E4EuAnc2lzsL4U4E7kTgxxKBO5vLjyWsd0DvROBOBO5sLnfWwJ0I3InAjyUCdzaXH0tY74DeicCdCNzZXO6sgTsRuBOBH0sE7mwuP5aw3gG9E4E7EbizudxZA3cicCcCP5YI3NlcfixhvQN6JwJ3InBsm0t7o+9h7R813C1ui5Xx1JnTb8f6/fBdr92s3N6w3O9fZ9xv7N/brJrOZzWrec2qSr8r+/MdN+hMGujmrnP2kW+r3/f1VkEOk2/HbxUz/C3GYe2DeDN2M3VwU9+MzK3wtLiHtW8F7yheOo5TTx/vKP3t/O3YcWyby3Q6vW7LZDK53t7d3e3as5kj6wbdjqNbW1sVPfDicPSZyxhN+pnT1x6Px9eNwNvZtX+Mz3cnVeNpdTsEc8fTmo0nzW6RXWOvnk2nnTzPXx5frVdrXNeqaquqeL07rZqbhDWtml6bd7V2TWdVM9jTms/Y9Nr4XDey12j96039A18T88SF7GEFVhsb7cjv7Ox07Va3tnnlZvCTB3LwQvS08smZOkTHYXZnHG9k6DKO2vng3W4dH8i37ejt48aGg8b7diWW4TVPB2ztxLnVZVw/Y+EJRluHt42N+ehNje8gatdG9B3E144ttZ0fpT0ajTpxxqVtgCEMHw5fu4/hUwaDwfVylP7l5eXr2ORCwW7HzAW7z5d+vx70bKzBoIaNnj5/p3c4qEHN6uzKxv6CnlYNqpZqVMOlqkF3xTKvwXBQ8+Ggaj8MXQoHwxoM5jWfzYncFPV9bIXahcG2xMX4UQsCrzyFWvmVlZXXYOHpx7Y92ILR1rGF3NLSjWVnvF0v+n1sY0fhw4wOeIvi1Np1K+2+ne36PQjnKBva+b7P+tHXn4su43xO3tt2eFKHV187FJlgZLxftzlr10mfr+3fyHI7ehttZ6PV1dXa3t7ujF9bW+tQBKg1XLtvnLHW4YPUOzhaB/EEt5WFnaTgaee02z75DuNGrLuN4fqR3o7HqMjAthnN6ahamU5qPtut2bRqtLyyv4kMywl4Zzyp1dXlGi/d2GSNjWxCg2H3lmqpObCjqq1z4BiL3X1/2o08scFvXG6OInjkUqcdObF1JSq+NvqQA7+fm8ylbm0OL7v6+cAfX+MDnsgEr1/HVpjJf9aZupVvcfs4i/qxKzx9+423fra+xZbIhrftayf22tEXe43BUfiIV2FHePWjK/PkYIQneOZjb8bUxlFby7GTTLC6xhEvg+N6KjoOXb58uVt4Fh+DGMgpAYgj+lkAcSqOHGZvAqqGm8Wtn6DF8RYrdhlLic7Urj2QV2Oz/bd1w6WlTiYXit08ntms21g6PS4jp+Ma7F6rkbc2NtOyYUhc1XS0UrW0VLNh1WQuFnsJ3drerOXlUa0trdRsNq3lwfL1Pe2gGFy3dT/x/T4ZG7wFwC6XsQ6otBPvg7CNiWE2CTLadMCAJd55i+vEIZ/G8dq48C8i+N7W4mUL7Ojry8HMvLnw9/naPhmFjvX19a7tREcfW/v+w1fIoNQtZtvGy4d2/cHlQ7tx42vx0k8dO1vsto0PJl1sxh9ZfNr0Jrf6bd7D3z8uYlPkzQcjuK0d/XhcunSp7r333s4e6yAbTSvTbx/blUs+D/nqV7/aKT558mS99NJLdeLEieu7LYc4J2hZMAy1SPEvIgE/c+ZMcdIGdvbs2W7B54oJblskR4DMJ/gWgYOkDbA28vZlxYE0mdTVK1e6sVOnTnUJSLIlIwcV++F1B9ilSzX6/vfqdac2auPcudpcWqqL40ld8y7o5OlaPnOqLl67VrPBsJbXVmpra7tevfhKndhYq7Onz9Tu1natDJc7Gw6LwdWrV7u45i2KWGYBxVc54B+/r1y50tm+sbHR2cjeRQRDXPHLxbVr17pFDo8etYPVvPLcc8/Vk08+WadPn653vvOd9eqrry6C72z/wQ9+0Mned999Hb7YwUresgmIs5xtbm52czazo+ynnA/PP/98dxCI0yuvvFLnzp3rdGUDaHXRpxhjxyLCxw7rj23nz5/vZLWtk+SjzYm29a2QlRc2Jl+xJbarxRimGMDlN/nIWouKfPARv7zxjw/GybNXmzx+hN+4tWGMDLsQW1tiW0s2bMffzeaC7LFtLjYRpL777rvrnnvu6YzR5lA/+HgFQWAsote//vWd/GEvMAT7hz/8YRekRx55pAumg4DD5iVNUJJgWLDpYJeDRoDNJ+CS1gVyPq+VldXa3tqql198sTODD2vr67W7s9Mld3llpePd3fHWYNhh8WHwzA/rD//1v67lhx+scz/9vjrxzrfXvffeV973zAeDujYa1n3DQU1HSzUYLdWly5fr1PpGt0Hefe5czXZ3a1ijhZvLs88+2/krBnxgM5+z6NQWoQXloH3xxRe7heUgEJccXIfF10GJx6YtZ+KjtLpsXhaYhf/UU0/V17/+9XrTm95UDz74YD388MOHQXfj7GWXHLzhDW/oDgp5cECwm430ORgUB43NAY/c2SQWEQy8irVBz8WLF7uNJgefGCG20CV35BRn5UUk1uJj/YkDHWy26YuJebphsz/5cCBbo2KK35y6tYWccTU8MuJORj7Zh789uWmbwy/XjgG5ZmNiASN2qPXlwEkfj7UkTuxht5L4tLW2XJOhJ7Z3zAtejm1zERhGMt4u1+50jGZQ6tgjufgZLUGLKLICSg9+wRJMgc58HwMvPYJIRh8dxr+6tlpXNze7tyinz56t0dJSrds4Bd7inFdt7O2jHc7K8koNllbqlb/9Rv3gyb+v0cVX6pGd3Vr58Ieqzp+twdpqnZhN68TJkzXxdqlGNR2Pa7y2VmcdNBsna9CdNF/7gXffDwvIgcgH/i4iB44FKubZjORnESWWDuScxcUoBEus5RX+N77xjfqP//E/1uOPP16//uu/fmT+xN0BxPasj2BnwbY5oUve2M0mPIuIzXjpwK/Ag2NjOihmDnonn6ynRfiZEyf+24SR/mG24bPpWN9sSAyC1a8Tb8cETFeF4p589Pn1zds88cs1P/v8+vgQHfxmS46JzB2EH5vMiW0wDuLtjy1epX3uBf3WwBghSMhOLwkIX+YFH4+zVOtEx9h7kSSBsxgcOBKWRMPLPDGLjB413WRyYEiCcbrJCbI+0oe7ubXZXUVor/u8xFnJh5Y+FHXA4RfoedVke6cGlzfrsfsv1OCpp+rbn/p0XXrh5Xrnpcu18Usfr7r//qqlYfe19mjos5p5za5t12TzWk3XT9Tg9N4B7HOX+V7+e57vdXM2syDaA0Xc2tjjZrcFlHY25D2kg18dyNnswyE3wYYRevnll+trX/tat8EYdzZ38CTukZETMU1uYxO+8JqnV17kJAegMfzJaw7m2HBQTUac5Fyc6KAbLpvoChnrcr252dWxMfP92jzb2ORqAbY++0J44rux5IFNYhn9qfGQCTYsPliv8Mlb4/EjeWd72vEBD9mMJ/Z0RDd7Y5MY2XQS39iSOnapEZuDnbFuYsHL4tPlAsH+lKBSygBtRud9KSdiXBvYYHD6KIpjufSzWdBhUdKXeTjwjEUXPv1scPra5iVKPew+iK1aZ+vS0v4Vy977cHPBmnv/OtzbWGoyreWNEzXcHdf05Vfr3vlS3VcrNbr4an3yf/8/avPP/7LGz7+0d+/MZFbjl1+t0XxYd2+cqOXpoFZnw5pv71ZNZp3+zo79M7y2wu4sZD4rKAk23/aN48nZS5uPR5F4iIuripAxsbSBwLXo1Z/+9KfrO9/5Tnf2tsn89m//didrPrrUNiFkQfPBmRieA1S++Bff8NFjDLEfT3LcDR7xAptcfKDPgWWNwIWF2AYbrxObM/5RBJtcrkD0kSukUHKRPn/Eny5+tj7HllbGPJsROUXssg6Mx3ZtucgVPx5+hidxxJO1Diu4+OiiM4SXnYi8uay/bFDmWpnIHlQffVQfJHXAGMMYYPcUgAQvrMYUfCFtxkuU9qISGbgpAhGZtFOHP/j6eA8io0KqzOvGjUmv4d9/S5RvlvbusO0uk2o6mdTGcFRveOBC3X3iVL3+rvvq9fc9WL//b3+3vvpv/l3tXNqsGs9qZbTkVt668tIrtXt1s1Ylb3nVd9qdWfGl1Zuxvt3GxYG/rc/abXzItQu4j5M+npYPDpIz5GztMwAbyCc+8Yn60pe+dP2K81Of+lR997vfvX5Zbh142+REAAfu97///c4uB0MO/sw5CLXjE33pa7d2dcYc8BLZxCQsxvsEG4VXje9mCln8qMVu13bGW7sz1gn2Xlq9wT9IB7HYnnbrQ2RanlZv2vgi1+rOfDvWM/WWuse2uQik3S4lO3tb42kDHl41vkUlXgVPP3hq420//K0ObZS637YM3c7WbTKD1y7qQS6p1Vmv2q7SxpOaD0c1OH2mlldWazab17v+i1+qRx55Q33nP3+tPvev/7e6+vdP1/jKZneH7llvbUaDGon+YFbl5rp9f+JHN7BvK3vjY2xPrIxbDImLfouFPzLBPKgOX3j7eNlkbCq+EUTOgs7+f//3f1+/93u/19mB73vf+179q3/1r+rv/u7vum9X2OTq5itf+cr1S3Q224QscickPCmwW3ti00F2t2PkE5eMt7Jpp271Re6wGi8589ootXYOzHa85deOXhhp49eOLamNo/D1a3N4Y08rZyzUtoMR2cikNp/SHwverdQ3rLgVqUN4ORJnw5JdlLEoSVBbiEp23MgsqttdN9gtP9zgmQ++8VZ3ZDKW/mx+48zveaHrN59kQ5ml0TlT3hpd29muq9NJ1elTdeE976knf/iD2l1ZrZ/9H/7H+uDPfbT+5okv1+/+z/9r/e1nP181ndToxMkajga1Pdndwx/Ss3c2/Qf27F+ZJFZ9n+NX5BIfNd4+f/zs1w50hR4UueDm8tvboHe96131m7/5m/Xe9763+0D3V3/1Vzs5VzWuQpBL8M997nPd1YyrGN/8wLIZhVyuu8RuF330xQ/2sOsoiq/xO/zxQz9tNT3qPn/kDqr7MmRDsTt9dXLGfvMtz2Ht2BTs2Bzc9Fu+tNu58Ld6Mg/7ML9bfhj6/bFgH1XfeMN1FOdNzGdxCmociWH9zSUOtvUiFTat1tG06ckuS74db7GN47WQtUNpe+hw6rpFMAdV9hC35c8GsxraYSbT7ma46w82dgtr0D0jtLm7WxcHk6oH7qn6lX9SV7/6lXri93+/Hv/oR+v1v/rf1n993z31W7/z23X+qafqvZubtTOb1M50UtPlqvnIGzH32bDvxmLNGYfNSuuLOWOI7/pinrcX8S013uBlrF8HP/oSl8jRY8wtA4899lj3Pv53f/d368KFC/Vrv/Zr5R4Wn6X4INVX075B+sIXvtC9nfqt3/qt+tjHPtZ9RhNbrRUbC5uzIbU29X2OPS1Pvx0edXzOGN6MtT5mnv+L6KB1Q5YcnxZtkHhiEz769SOjn/jGHrZEpm97xtX9td/KsQt2q6ePz7ZgmDsIE8bt0LFuLpxJoNUojmlzImTcosoHTOHP/EE1Hmc7H1wpB8lkjC7t4NOXudamtj1wt8mwOmw31ZljsU3GWxdjxS+bk89J+ONDx2HV1aVR1amNqgv310999CP1+3/0R/W+J56olZ//cD38j/9x/cb6aq2cPVO1PKrNq1drvj6qpVPrtdNtacNaHlSNmsvZ+B/7fE7BZwdkFkB4+JVFI6Z8x2ss8uE9rBZXsVK3eJG3GZizSbDlW9/6VofvisYGc//993ff1MDH5+rmd37nd+qTn/xkt/G4t8XVDBwLuovt/nqwMUZPcsRPOObURxF59mezCk5q8mnnaglu1kfmFumhgwz/Y2/iTl7c04dDD3z82tGBTwm14/CzvvGQgxl+erXVaWdt0IXEIJjq2ASLLHxvRekKX/D7tXlyt0O3J3WIphhqQVhIyKfxnM1ubSx8ePBabL4aO4oEE57ABF8wYCcJ8FAOsuA7q5KFYYFLhKDDWV5dqa3ZpAajYS3V3n0xNpLxZFzz6awr452d2jhxqqab1/Y3gUENYGxt1yvXrtWVpUHVmVNV21fr3o99tO7+1jfric/+ZX3wrW+pwYX7660f/3hNr7xatbFWtXOlpu6IHe/U+spyjWeTOjVbq6GHpJsPufkR+42LE98zrua3ePLPWw78+vgUcSXL70UEW1ySEzhk4IpV9IorPDf1uSvXjWp45cEix6dv07Hh/Pt//+/rAx/4QPfh7gsvvPCaMykcOhUEwxgd7Iktrd+H+UCm9TkHkrdq7ELwcmDFp1bmMGzj8GIHGWuO3cYS36xFc3KgNo/YgS84rYx44RXv2KMmK/42gdigzwf89PGbX9pk8Mq5cWPm2uPNlWV0OB7YQQ9+mPrkyGQuPnRG3MLLsW4ugsQx3+tzgIG+ZRBQhjLeWBLPcbwCb7H2iZMh8gLgvbuvON1lmGCoUXSQkwC6HABkJMW8MYvC4iKnbXPZHu/WwJlmaanDt7m8+MILNRlPug9sx+5oPHGlu1V/tG9XdzBtb9czL79cm8OVGt9zbw2efboGFx6s8/c9WF/50pfrbR98vM6sLtVkNq4Xt7fq/Maotra368qrV2r07Iu1cm67RkP377xaw8mNy1J2sldiFX5kYeqLL0os9W0uibH48NnXrPJy1OYiD+KE36LLgpU/sfSVq7tybRruOaGPbqTtcQC63dBl3h27H/zgB+tf/st/2dVsg/vMM890i1eO9GHwlU/xmT6+8wG2OJtbRGTwknHDId8R+8nTx6fwqeXeWhIf7UWU+LXrjz5y/IavaLM9B7e4yh372WGcr3hgkqHfmDl4fFCLWfKOT6z4BSc6+YHfpoJfjSf28lmbPnrEHD9cG010qvHAZSt9iF3kboeOdXPhBGM4kMXJUYYzWkH4FEbjU0sCilP9Gqbv5RMAi0ZyE4gEO4mzydFh49I2rw0XliQk4N1ZbLzbfQs03VjvPl/xDujqlaudLLtmk2ld3r8t2+cj7F7f2aid7e1aO3u2Nu55oL5/bVyrj56rjelOfeDDv1Bf+rPP15/+yZ/Urzz8urq0NK/pyfV68umnari8WpPLO7V2z0pduzSuze3LdWY4quH08OSKEX/5zcccDG2cEnv+ZNGT4bdYLCLx4RNe7cQ2sROz5Ck8rkS83XH1koPAc0NPP/10pw+GxwNcwZAnJ+5sowvJnwPcQaJNNz3I2sHHBr4tItgOPjmlN/jaZMXJmL7CBryJo7guIrIO6sTeeiUDQ2zZjfSRNW+cnGLTpcs4jMjhTT/HiVjJIf/p4BcesYtvsODb9OEjOsRQvCJDzqYjpgod8BV8iQUsNvEjx1RsSz46JbfwcqybC8MkwP0NNgILhmECFeKARKsFT0AsDIsUtQdL2xckAUhC3/KWt3QYghg8dRJlHHnQzOJ3RvasEJKMbC6SlDb76dhY27uMdvaFJ9hIO7jtQnn59Nm6d3dYb/qFj9T0nuXqDuNTD9YHPvqR+sGlF2p1XPXAYz9Vtb5SMwt7MqvZZFiPPPzGGpxYrV3PTflMaEFyXTXcdddd1z8Uja2dYfu2sZ1vbHTgWziegclCDO9BtRjJ00MPPdTFKosscZdHeMkPTM/jsEm+ySX+cHyr5Gr0X/yLf1G/+Iu/2B0ENhHrg02x32K3DhwAKHq1cwnvA2J8i4gc/fy3Nqw9fTZn/fFBbJJ/vtHrxrijbqTLZmA9wbNpwqND3FvKmmETfn488MADne94YSlZV63P7OVr3lbG9/Bk3akRXlj8eN3rXtfZYo6f7GCjWKDI6jsZOOYSG/NwoodfKBif//znu/6tvCy+1rwVpP0rEs5aQJwVSAduSzGaExzPGQ1P5vq1uSTQRmSDESjB6PPiCy98C4kO+hREri2tbjJ0KNqZoyeLwVja6sloWA+/+x1Vd5+r0WijarRWdf+ZeuRjP1NXnnu5nvvCV6umvoKqGi6t1HQ8rUtbm7U1GXdPjp6wsXSabsRgv9tVdLOHH32/MWRRaLPHgnDAxgfyRxW8zmStz8FWW6xyqsivIrcp7ELekrDBt0dOHB/96Ee7A0BOEkNrxKKGiWCF+ILYAdPBxu+j7MePN3EKXtZC+m0Nn8/W01H4cMQVPn5tRA7F7ozpwz9ofXcCh7zEJnah4EZP1p2+9Zxc873NXfxp1QQLtkJXn6KnHT9orJ0/rJ01fdj8LY0zPiXBd3Brc1zJAS5IEqa+FeNhwCOThaOfwDE4eGrjmQ9PdJpPslo5/Eo71t+c4od6t2a1c3K55uNrVVvTqknVbDSu+3/6nXXu9Nn6yp99tuq5V/Z++3I4qtHyUu3WtCY16a5yHGKWaGIXOzsD9l/YqSRmhvHRLybxOTGxcCw48xlr8frtxKLPCwcGXW0uYevTbS5nUFcy7uT95V/+5fqN3/iN7orG5iGe+MnBTJsdxg4iuCkHzbdj7GYn7OQu8+nDQq2P5vhwM4S3xc/aCUbiBKvNVfiif5FPmWvr1rY2z/zAR79Cf3SrzdONB7WYaXcT+y8ZC387dzvtY9tc4iDDBCBnJWe2OJk6huJJEQRyCR6e1sk4jg+mMx+8llp+4+ZzZiWnoNjW2knWfOxJbSxz0UcubfOD5VGNT6zU1c3LVX6FbjSqVyfXaunND9fjH/9IvfLM8zX50jeqLm13Vy+D9WU/Qdf9cNTIt9rT/Z+63N/s4Lf+0kFfbOJDp3efP/PGY5uxjBs7ioKtDo6aXjgWLpzgaqdPpr/ZeMv06KOPdn64BM/VSvLRXrkYa/2NXjLh74xa8IJXib1hZS87k0PjxlDf58gcVEcePpuiBzZq49LHD2/GEzeYKPbpx2fx6fOFN3VrP2x6UPRo4wm+cW3YfKCLzpToC79xMi1ep+AmX/ZW0k0yL2KLY2rGWYyMSs3QdoHajFyauXxXnBEQ2YNqsjBy5aKO086C5BJIbXN04FPowofHuODCpFeQHRzGUGzBh8iFn3zsMIZndzqpmSe2x9M65QnoYdX21I0yVQ/+3ON1+g8+WU9/+vP1hvvvq7r7bTUdumGPP36ku2q+O63paN793CXs2E93fEictvc/jDaXWJFhc+zRVvgd2/EsouCLkysNsZFLddptjsW3xfQ+PrYnznjg+kwjNopfKPlTk+EPf+VD3fqhv4hgJFawEg95hct28WBnYpIYGT8Kn/2w8CrImHZ0iVPG1fQkrmTZGN/wZr3CYKMCK35Ep3FtPsi/t6YIhnEyCn1tjsxnXQeLTvroIIPfHB3B005uYkun8BZfbmT6FgUPYmcQA2O4xR7n2kVFVl+g8aQchJmxBM3iwK8vCEr7nj38ajzRo1aMJXBJtrrFyHx0Zs54dLI9OpaXV+vaeKdW19drvuKgrzo3OuFGmao3PVCP/vwH6oVPfrne8LMvV/3MrIarK7W6tlInfNbgyoWdywMXM/+AYnd7toldYWaXBYK0xccCZKt4Ie1FlBzwC2905Azal82is1AV/Ba+WLHBZxNsiG34zeOzRuiwuOEj+hF/zZHLgZgYdAyHvPAfP39hkkHasFByFh+Dqx/+jvGQF3Zl/WHRJxvcvphxfrFBSS4S2/C3fXGKXdHX2ta2W79gK7DatcCG4JuHGfxFtse28KZ/K/WxvS2i1CKzcLJ4OCKocQ5PHBfEtPEdRTDxk8subewgCi7eLH51dKpDaUfGuDOAEmr1GtNnA4KrPRiMav3cudoZzbrPbteWN6q2J1Wn1urRf/Rz9dwzz9S1b/5d1YuXarJ5pbZ8zbh1de8vRnbH3SYTPa0tbTzpS7/ve/wwHj+D1+ftDO+9WKjyEN2p+Re90WFOwU8uC97mYVw/G4vNRnyMZS1EV6sv5sRWutrcZf6wGr8S/1tbI9NiG8uaiI/hO6gmG2z8/Axenz+8mY+f6fdlMw6H3eKV9dXOZT76goNXOz5HRp0xMniU4Pf9DoY6BCN4GbvZ+tg2FwbZCS2mdveMcakFGllgCmqd6QYOeIlcFgQdh8mHNzr0++2+ijYJ+IOBzxz5jKnjI9udnUY1qN3prHaGy7Xrva/9a3W9e2tU731HvfMjj9df/vEnavrks3Vid1QnT2zUeDaumQ3Gj3h3P3S3Z2f00K2tJEaxo+VpbTePxCkLtN3cu8kDXuKjTYCuVp82fcHWhpmScW9/Ype5tMUHhjF6gm0+NsakyKjbkvnD6uhrsfHqpyROsZeMdvqHYRuPLW3bGGxrO9jtfHDxZAPOvLnY1bbNH0Q5wMmg1Gwgn3lz0WuOj+Fng3VhTMkJtI9FLqTd9jN+M/WxvS3iHKfaxcNoTjBOWzGvr+YcZ7NhLDIYPjk6oge/tjkbG9IOL1xvyyxgfCG69dkT/thFRxJiLjaThRMb2C5Z5PBNZ/MaT2fdV8t+/3/OT1dIQ7vGrN78Kx+tv/7m1+qZv/ireujeM3VqablGK0s1XN6o+e64BnMH3l6MooNO+EriRG/eQvBBwc829phnMzJOFrX+dwO9lz4+n1xptFjGYLZxS4wT/x7s9S67yLORrfj1kweMrb1wyaTEj+uAvUbilGHysMmLF73xxRxd5rSVo/DZiocc0ucHMgY/4+ZQi9/K49ePPfrBbu0wT4f1qJ0carM5evAEn7y5xDfyavLBh5F2YhSb2BNdeMLXOXULL8e2udDJOIa6D4CDuXtQ4ONsgqROcATPJfUi4mB3hbC/65KlQyDaQBnHS2fwWx5jNhy1wt7IG2engrIxsa/lhRc5so5ln9/iqcm4JvNpbe9u17KDEdB0XoOffnNdvWejvv3ZJ+qBtz5a66RiqOMAACAASURBVG89XVcvXqrJ3Sdq66WXau3uu7p/aYTXTy4/k2zzFgofjSkZI8dmNTLHpla+mzjgpd1Q+Rb8xAQWve1Bqh1dR+WPrLjKYexnFww1gqWNh/6WjsLnJ3l2IjjiknjAS86CZR7dzPrD28eHHXn45tmhwAw+m+jkq5K84EPkyJszFjljYoWMJXaw+YLXGDzz4c+ceXEwbyw57gD3j1fzbMMb3a2fMPHcDh3b5sJwRgi4W6N9oKf2aXmcStASYIGzEeH1g0OLiKz38TD9Ur1nVNrAmxeU6EjQ4btLUu2bEKQ2n+A7QyN4xt3dipIUB4W2JGTjkax8QPf8yxdry41rfjLxxEYNJrs129mutcG8NmpQQ4tgfbXu/cA76sp/+ko994Uv18rZ99arNa1nNye1ZZFeu+LH6jr72+SKqQR7pgXRy0c1wssPNduziN3MJhf5zCNx6YQOeBGT3IYvP/HPuD6/gy2fniXyjAoZutwwt4jI8CHx45OSdROf2SmuanmWE/3k+jAd5NnJrjwzg5fN1o04xie1Ex/9fBC/o+yHz3briA6/G2zdRi/8HOT0yoU5uMkd+xTj/KMXpQ8fDvzE2tolk1y2PpDjG3y2wBRPvGTg89EagAffvJzBNW+cjeGHAZcvKOuv69ziy7FtLvQyiJEKJwQ4C4jBnFGbjwMCgS8H6mH2k7UJCK5aoQMJSIKCD8FkD/7gZxPBawyv4Bk3hj/YMNjETklJsFvbcxAEa315tU6P/Ij3qHbW/C63M+OgpoNZvbo8r/f8yi/UN778VH31C39dH3rsrXX3Qxfq2cG06q6TNRoPauS/pQ9JLh1Kaysb+3E1Ji7xVa2fuJg/iOQpOvgLN7qST7aljRdfylH5E7/IqGFlbchB1oNx8yg+6CfXB9meMbaRUeJDcMyxgZ3Jc+tzdAarX7MPRrv+yCPjwWc/in64Cr3hS87kRFshR8YmGh9aub7t+ggvvsgkTnQlxuYSV7rCn9o83ezBhyf42VyO2nw7Y3ovx765CKKnYu2Wzg6ClaD2dHdXNfhdjXhWYxFlIdpxXQ155iKBEJQEFYa+4Ji3q9Pv+Rd3j6JgaQue+QQWThZNni1KsC2sLJpsWuSW1ta7K5d7ztxVZ1b3Ppyt2qla3vsBKve0bNdOnb734dp+/xP1F//m/66lJ5+v9Y9/vO69e1zX/GVIrdRq7dlMXwg+e/jizld+sDG+hy9+5EDlk427jVN4D6o9ByRmHjJ0NqQTRqunbbuiYY/imS3PtSwitrBN/MSVruSplYsOteLMCt9aWkTJmXznOR466HXwIDxil1hZm+Y9x3PU/xaxFVl/cOiAg+hRQvEBH93mrG/xPIiPXGLBHnY5hjwEqs7mYF3EdthkxNOVCB/Y1PpnHr9NJL6zDZ54wvcMoOMCDort8QUG2VzNZ/xm6hsRuRnuBTyMQJzjTL414oixPnGC0Ulwf77fh0HGolbICnYO/JY/CUxgbAQKeZT5VgZv7HSJqSBj8U0/B746Pkz9+r97WpzJhMEJbS60g/IPSJ63XZkvdx/svvUXP1InH7innvvi31Y9+2qtr63Xdvd/RnvWBH+vt6fPWLfovM/eP1u2fLxqfWMvfx2YiVPwDquzqMnCavHJBD9t+PJAjo6jSBxzQ1l4YbaxzbgapgMjpZ07qM1eMuxhW3BbP9JOnTiROYr6+PitI+NtbIwHnz1sCX7Go6vtZ01GhlxL4TWPxFOJz+KUufAGE3/aeBxz8MOfOXyR7ZTs9/tjmTuqPrbNJQuFwXHAmMByRiKT8BjFKeVmjccXnDahh8kHP0lIMFvZtFsM9iqhzMEJaWfc9clwPqmBh4q8Fer2FbwuDJdqUHvvpbv+O95cF376XfWV736zxl/7mxq9+mrdNd2p1b19b++DYVdUzmZd2TsA/YbMsr+D9Qt43W9w7lmCZzyb1qD5kW8ziZN2fIztB9WJVVsHhzy8xI/fxhT8bVwOwjaWqyAHARkU3FYma6S142bwk4usv2C2ulr7zUdHZCOzqG7xybNNHexWtp03zt+W+v3M9XW0somPseCzocUyHkrsWh9bfHzh0W5x0u+PBfuo+oYVR3EeMc9ADmRRayuuYlxyxWGOZaE6gC22NmBHqOnw6ArGQfwJRoIYmzKemmwbdP3wpm7x4YUix69hzWt5OKnBcLe6D05GfnDbJjCqtVqq9VqpE8v+jnS15pcu1Yf/+1+rJ09u1nf+5i+qrozrxAuXa7TrrY8/q9/bWGiyvU32fzDc19oDl+E7/udo7yrJUsUzG45qsn/lmI08C4/N7UYZ+/u1mDibKdr9GIl5cig2nd/7b21uBp8+V1JkQzBsOiE6E2PxZYuTU2tLePs1OXxZh+lHH7zYn7M8/LT7eP0+vNbvdr7FNo5XCTY5tvX9yBpqsfCmGI9MeFNHxnzsyhzdyHja4Q926oyro6s/hvd26EZmb0e6kWkN4GQSGYcZnjFi2jadlFa+gb3exA+j3ZCyMBOUVpd2SkDwKXRZhCh6I0uPt3Io9mYu/MaDoe4W02xc05lf8997pmjm0mNetTTbe5fUfYwyGNWgey5kVhfe+/b64je+XG//zpM1ePRtHkaqmT+j3//nEhuHlLpfxhnATXrdD4XbtIz46tvGMxjWrGbdL+ixTzyzoPiaTSF+do4d8IJPEdM2boktkbTNi0Fk1Efh40+uoz5xhRudbczZQkZ9FH7WApzWj4zTGX2xO9g3g8+uLs+9+z4SE3OxPbr045d57YyRi2wrx7ackIOTeKkj047BjW2tvwfxw08etMMjvsFmj6If3FbfzbaPbXOJYQlmDGBcqA2uMX3EsTbA4T+oziLLAsEDJ/r1gxUetaCr8apDabc2ZCw8mYMR7LbGPy1/l3YD158yIpuEdyyT8byWNNbX/OJ3vf3d764//NKX6pW/+qs6/+a3CIL/re9+/ztvyERn0B3EbHaQeeJ6ZY/J85F+1LvTYRvauwhNTJ01FbazL+PxqV/LE942jniMRz5Y4RGDtvQx2z4ZNrR2wBbTtqYDpcavnXi3mG0bPhyl5Y++zMPJWGpzR+HTlQM3csbadh8Dv5L44Q1/6vjABsR27fT5YzPQJwOrpXZMu+2zJ/xwzQU/utSJf3TiQ8HKeDd4Cy/H9raIIwqDYhw7OBOHGNkamsWgvhkKlrqlPm7mjEdHa1crH3vMGw9/amPxJ7zwgxHd+P09yUHkY5jxeLr3oy2uikbDuu/CA/XGt72tPv3Zz9b0mWerlvY+re/+I20/TpaRxdH5cf0zq3+ow7Y2b2KCP77EzoPsasdyCc8PFF/JByMHTxuP+N9iHdTu4rN/4CS20aGOXrL0sSfjN/O2K/hkgxss/XY887Gj1X2Q7e0Y2ci344lJOxa90d2XbXHwKGzJiSHyrVw2C3oyH99bvNiRsZY3+PE7PJE5rvrYNpcYlCAnCC7xcplnF88CxY9HP2eEYBxUJwD4gyEZKEGKXHgT9CQ3dfiTTHKxBbZ2vx89LUb0eAzag4szCy8bjGOUee7enbofYclRs2eiK5TV1frYP/2n9eQzz9QzX/xilf8s8kGt39H15/bTyf7bof3L8fn+QZ6NeP9M5/8hlaXmjMZ2Mff27mZiy6icYRPb5NFZEx5q57TxpOw5dvirWNHBrsQ2uNGtTx9sRd9cbDkcfS9/+LPeIhM7gw1DG7U6FmFnjg/By5g66yljWRf99Wc8c1lHGWNTCtuj5zD/ybUfEdAdrNjTX98tPh2JQ66MIh8/Wsx27Gbbx/a2KIbYFTntwzIBYvBhxPk4qb2IBEyg3RfjoCFnrA1IEqYWOHPqJIhM+MOr37bZwG6UJJGLrLHWL+PD0bCG86UajJa946m5XcXzAC4vR3v/Lt3p6SanNXD7/mipHnjsvXX2/gfqC3/91/XAP/tnNRqe6/7XaNnC4dtgWPN9m7uDjk8wnZ3p2L8dhobJbFJLwxv36MRvfshJfOocO+AFf/xKPPjW+guHHebl2Jy2gncR4YFPj3ZiSyY6EmNjwWxtWoTPNvLwYzf+2BxMeMasCTqQsbS7gUNe4OZEmXWkRuaCoYaJ2CNmLYXPWOSNwdAnm7Zx8UnffMbU/FC69dF8ThKfwq+GgczFvsybg9cn88rt0LFtLnHepuKmOIvPzVjb29vXg8V4hsY5vLn9323Yi0iA4fn2AKY7BumgN4U8PjoEnB73q+BHFgZefRsUPhg2LGPsw5N7XNyQlU0Sj/s6chDS414edWeLn6y0iCazmk/mNd2RzFENl5a7f3Acj3drealqaXenRu4/WVqu6Xi33vvhD9effurP64df/GLd9+Y31cr9r6vd+bhe9fW9O2VHwxrvTGpre7c2t7ZraXS1+29I/9o4G81rtry3gc/Hs1oe7d2ib6Gxie1+eFvM+LWI+J9HJRx8OQCN8zNjiaEcJ3figm8RJRdi7kY0NiFxhSMvyYlxuaCDD/KuXkTyyG8y8JNDcrnVP3FofaKbT0etv6yp3KtDT3zOhsmHdv3p48fnRrd2E8ixgEdhv3n2sl2bDnnkFx7xEWv2Jh5ywy8yeNlCH3k62CN+5IKDV8k/NpCDiR/l+ORz8r4o9ofNHdvmQkGCxBEOCywnEOPbwAsCw5Osg/63qDWao54ZwZ/nWRJgehOYJI0+wcRvsQmYObxZZAmepBkzJ1mCjcjxBR8eWOxWkjSY7l6cDPdumNpe26ruprqdeQ3dMr682m0u2+O95452r16t0zaM0bAuvnKp3vKex+qPP/OX9fnPfKbeOx3XA8N5XRvM6wUPf64sd39w78NaGx0a7+zWZDru/md6MpjWfNmbonmtDJZraXjjF/UsHD7lf4g64QUvfMxittDJWqAWqg3APJ/FR5wclOIhPornYRaRO0HFFTabyIgdbHphaiNthF+O6Uyuu4kDXuRXjuRMrPQROb7Qy5fk2gHHJzqsE/4soqwBfJ6lknP+s5V81g+fkDHxw88eaz1jbIOX9QhDbPlvTDysMbZZ6+aNs13c1PDg2DidQBxn+IxlnbIj65TvjonEm47oo4csmxAMhc6fmM0lu6/f9WC4AKkTVMYifXMcFjwO5PZrTiJ12unHYZuM29TNw8zC0xcgRWKRg0yABdZtzvTilyB8aeMxR44MYhPbzLFZYmM7X7Utqiubl2s8mtXpc2frrhNnu/vo5vsnWjZPvY2oWW1srNXszOmabm7WxWeerTe+7Z21+YNn6v0/+7P1+c98un7h5z5cG2trtbGxXtPl5Tr9wAP10qVLtbyyXlev+IOzM3XXXee7b5R2xrs1rknNu5/MnNeoRrWytLfo+MAuducvVdi7iByUeD1eoMYvHhatWMESLwe6mMuBA1SxwI+6/R+Ph02tB48MwKNDXmDRJVZ0GKPDPD/cAm9uEcF1UPEdHh/IGMtGItf4YKr1HVh8omMRwWUzslG6dd7ayJqGGR/whN+atM75TI81A4ccHvNwIssmmxEf3NJvXvwTK1j8ST74yBfYcoc365QsvBYbJowcc+yhC6/YKzAVbXzK9773vUXhOXDuWK9cGMrRJFfwLKo2oAk84y0iQRPo/KcQJ0NtG0+CBV+BgTivnQAZS3CMkWWHBBvHzyZEv7Y6GLCRBSrA5PEYz4KQXEmDtT0Z13g4rfPnz9a59TM1cuu/P65X79856+HFkT+iPnW6Zie36uLzL1SdOVsnVtbrfbu79Z8/+5f19Sf+uj76sY/Yfeu+s6f950ad8wX3isV/rs6dO1+nHATDqhPuq3HlIgROOHMfjO9dHfIjZz8bajaHzqlDXizCbBT85jP/yCr6SrDwiCkZxeJeRLDED1/wxVBcrZkcAIm1OXyJOx2LiLz1ZJNQyMo9e+mURznW5yteGwI+xdo4iuQahtiSyQFOLgelNr1yYJ4/ZKxvdlg/xsKPNzhkHPixSZ0c4Ccb26OTfDYuOhLnrNOsa/L8lTO4bLDRZCMnF4r9ZNgG4//3zYXBKMZpMz59xmZenYPZfN+5jrF5wYvwohbLAjyMIifY0acdSjsYwTUfu2NbEmYuuObIzoaDGvnl//37Tfb+sH6w96Hr/p/Md19VG1pdrnG57JzU0Kbxzp+qNzz8UH3tS1+sDz33XC1feKBqZbX7CczV5ZUare6d4boPc7mv+HBUSPb34nm3y7zWLrbFv/gQv/t1DgT+J078dzCSbeW1zeGVc7KJXx83/cSVnBIMbbLBT1xjQ+Qzn/5BNR7+puDRDmZ0G9M2Hj03g5/YBC81PfD61OLzsdXbytAd+diTfmKT+LVxDk/8jT3RQ0fbDgY5Bb/5UDsf+24mLpHv13tHbH/0R+gz0GKzyyO7ZTYd/baNL7z400+NV4nT2vjs3nZTfMh8eKI/vM4EChn85rUj17bJ4IEd/FY/Xn0U3fj4mHL9XhdXLuzz9XIjc3V7q7bHk7rmz9e2dqvcbbexUR/60IdrsL1V3/iDP6i6ttndaDe7erWGQ08miyM94+4b6+5KBaavr2vaff3d2qPNHvYmD8ZupiQGwUvd+oynLTeDy46UVjZ5SP7MRVf4k4tFeiITnuAEtwPdf8kY3uiI3KIaZmRgaMcXbWPtuBxYe20uMk9v+LVDwW/HzBlH7XqNzqw9cQpP/IeTNn3IWGLaDezjR3dwyeGLzvDebH1j27pZiQV82antdtlF1dlh1e1OGD487Xh21r6q8OFNwRP8tFus6E+NVzu8bTt6MwanxTaeuYxnbD7wNbGb9PfPYJ0Olyluatkbm3oPO5vXyJnTh6R+nsHV6GRY937gp+unPvOp+tQf/ad61z//r2pw5mz3gXAtj2rXL9mJo6+8c/XqMraDdZ+LS+a9qzc2synxSSxid+f4AS+uMHN2JZOFGD8TL3XwnfXI5Or0ANjrQ3BiU2wJdnv2jL0tL/7IXAc8oBEZdfhb7Iz1dbT8B8B2Q7E1OuJPxlu5Pn7sV+NXi29kYxeM4GcsWOmnJhv5Vrd2dGjjj0yLFT2RDVZk1W0J363Ux3blIlh2uXanZAgnYjieLFpzbTtBUIf/Vhw5iBcW/cFUoxa/bQfD2GHj4WmxrvO2l8YO/PS7z0T2F47vo72fsUv4ephJ7n85c7Yee89jdenFF+vSN7+995mN/6zurrTGNeTH9Q0lVvzD+rotvUUWn26mhprctGe9tPtabxazL9fX0ert8x6lA5YzrsLORdh4ogufchR+7MGbOERH5vp1DuDUWTPqtMmYD8WeYMfW8KfGf5DNGQ9eyx8sc9HT8uENZn88/Vupj21zSVIFPoUhCZIaTzYf/fD168i0joS/nSOH1G3gIpfx2KYODp623drQymc8eqI/+jLvx7VnSndbLqN8oGsRs3HPzuFgWCu+LZjPascfqdl8bELd5eqsTr3rp+rRN7+1/uwTf1z14svdBjTzlHLNa1KzmswcOPvWdW+LbmDHZnaJsTrFHLsXlfCq+RQ/g2ssdMPnGzoWYR80FwyYdIYnetStDZk/rIbB7/je4sRuc62+2BBdh2HHjszjj80H6Qk/npToor9tp08m49FjLjYHM/r0g93WLV7aaoQPwYh8dAYjfXzhiVwnfAsvx/a2yOWnnc8lsnZ2YzshI9XZRdtaG2/GDrM9Oype+C7HjSGyrprUGevjRH9wzLft6GdrLqX7eAfxd7juZ5kPul9u6Z5c3jPqxpXLwMXJrLti8cZpdv2eG3fx+if2pZoNV2v4jrfWh9//c/X7/+d/qOk/eapGd7+uhqNxLZ1Yq2vL47q2Mtl76jpvvdTTpb1vi3qZ5EdL7FxEnR8H5CIfICafMMQlOUt9FH7ylpjij4y5tk1H+OVCyfxhPoRfHfvwJpexO9jw8KYchR95fC2+cSTeibm6j6efMfItf+bUsSd266NWNv1WLnE11293APsxpRc2XHwKij2t7fBbnuDcbH1sVy4xKgshwbAT5gOhOB1H7IjZKTN2WM2hYEUOb6gfJOMJjEBGJuORiz59+OFr2+GNDv34px75OYHprFa6X1vYuxqZj/Zv3R/6RGTQ3Ugn2LPxbs22tmtjealm00n5HGa8Mqwrp1ZrfvepeujdH65Ht07V8//hM90v1dXSqK7sXKyLK1fqldXNmg92uquiubdVw5Wq6XLV2J3Be5uHzSB28juLNH4eVvMXvxKe+Jk+nlDiZO5myVnYPRihxJi9wUkNX2wV7dhwWN3lYf/RAiea4PT9oTvx0YbNrsNw23Hr2IenZFDm+AGTDUhtTm1O0Y6eyMJRzAcrtbFQxvRzJaPNt/jS5j05x0M2tRN/bDfGl8xFR+xNnfGO8RZfeue7W5Ru2GOMxePGK07n/gJBkPDwJPgChc/XnXG0gXxNM4lSJ3jZtDBq04PCIzB0qunHI7jadJqjV03GHOwkzHhwjWnnw0tyEsqHif8dms1rPp7UdP/SOwspdsMWj9nEjzMgi86/JWzV9sqgnh/s1tpgpVbvurt+/md/vv72b75a9z7xtVq6/321W1u1tjSo0XxaV6dbte7t0U7VaL5Sg9nes0az6ayGa3s3etGVwma26y+i2MluvuEXI/kU18wnbmKace2j8odXbNWxKTLiaAw2vdHFluQvvIf5wEe8sMjnhjpywYUnB8bcW2MdsB3/UfhZI+SCx2byiP7YzQd+Zo7f0YU3fDDTJwOj9dkYP+iDBUc+8MVubQSfPbBh4IVvnLy55IuMYp4OmOIG01jm9c3Dux06ts0lhnPCHYY2GInc3n+2KAciY1ECzDGJdffmIiIHw+3UuS1a4DkOy3wCDSebgBue3B6dPl426Que4GuTN8dm9iM3fbEPHx52Sho+fkqaZLgVPIlgEyzzCG/m3LyURLHJDU1wt5dndXl5XM/NV+rB3Vdr5X2P1lOf+MM69ad/Xm987HV1eXi1Vl69XNPd5fr+yUn3TwErm/Nam6247q/ZYF6T0ayWV/fuzBUHz8qw199zsIcNi0hMW5vIOpD4L7dizyf2wsfrrl5Fm/wiIicX4pdHBeDBag8CdtKH3GYvP3QfReTkgw75U4yRF3f+aMsvvW7Kkwu2R/8iHWTly9rhq5zTRUfWBHmY4s1mfjgO8Hu8BV946SSLsp7IkM1d6+LPDzL4+Uc/H+gRu/DQgw8GX4MFD7958vIA013o7BMLOcQTm9gDu/Wn69ziy7FtLvQyKAeTZOg72JDEcFSJ8QLEOcFQFpFEwBMAGOQEOuMwzSVAsIyxg54E27ixvp1JFlzzSNs4zGBlQZhLAoyRMRY92mRyoLA5/gb7Bsa81rtN71pdHuzWuTc+UBfe/mh962tfr41vPlln3vZgbV4e18rquMYnprXr6dzpvKbu0h3Oa+yH6aazqvGeHdFJD71sUy8i8+GNrxYrm/XFQBvBx8vv+HRU/vDDQPzWVmDBMK+GmRjrp5g/itgJm0xyQ47/dKWtrwTb3FH2000ma5UefURvbIalrUZ04CVHvxL+8KQf+/AH3xhf4MhHeOCRM2cMlhqxKzYYI2cMLxltJToyF9uDG/uD24HfwsuxbS6cUeyMbr/ObeE2AMRBxreGm7NrOgP4C4yjyELEb8Py/JLd1pgDOotJEugxTld2aM+DuD2ajfSS0RZYu38CS84uj/ALLBzjkTMnMeQQrNiUW6vZQYbfKHpcCZhjP3xXR4PlYY1rXCuzWW2cHFddm9fP/Hf/vP7t//S/1MVvPlnv+tDjtXRxs5bO3lW7991VNViuc6f9c8lybS0NauxTndm0VpZH3SKmk24L0DM/9B1FzuD89MyMMxx7xZefiS88uPj467Zzjxd4poUfi4gNYgk7t9qLP2xzWTtZI2o5pRM/vkWEHyWu1h958bYm2QwrZ3+546MxMm6FX0TkkTjJsefOyCF6+CY2IW1juTLytx/yosBib2zWxx97XZ07hugQVzaLUWwXC34hfroSwSfXcLJO4bOBr/yMbnJ0WX95lswcfnlgj3ntYDjubpWObXPhBKM4zmEHM4NzAMbo1kD8DmSOSNhRBAO/AAo0fPoSCHgougRGoC0uBwpb8OiTRRZYFm6Cm3744SPjmYscXfiSRFdoCFbk9GOTmiwbyOEHP50td/faDdYGVduzqsffU6PfPlnPf+kb9a5fulQnZ8MaeFZrtFazwWqtntn/AfBRlcNuNJt2v+cCE4lPbEtcuolDXmzwZMjLH/uTv8ibb9vyIB7GxXcRORjEg7wDQZsO/WC28omnMbE6avOCJa5sSr7haicPfNM2xjcbZ9o3s/4c4PDJtuuJjf18Z0xc6bRZkDvI19ZvbfFMIZs1Zw5GfJRfffN8Y1Pm1CjrNPkRV/zkyPBf/zC76CBzO7R31NyOZE+GMwIRY2KQWjEuAWqkLVkpPbgDu3AsUrsw+TYg5oy1tTZ8i0jRj34KYhM5FPnYFKzMmY+82jxcGxgZ/egIdmSNpw2nLR469FTzZHdSu4NZze0P956ot//84zV9+qXa/YM/r9oZ13h3XEvbu7U6m9Z0PqnpyJ+a+Gj4xgKgly3ipGjTdRThjR+xjQx5mH1/5CC5iG+LdFgfrnaclWOPOrIZo8cYvcmb+igiAyNyamQ89mcMX3jjx1H45skkDnBTgpf56GO3g1sJb/TEz9hHNjxqtuIh2xJM49a+Qk7e+IE3umOv+bYdbPjamUttLDLG9MPXMd/Cy7FducSgGJO+DQe1G4G+8ey6dunw9/nii3ELNCW7efjVSvRFR/gjr6YXpZ1N0bjkZD47urHYSwZljt3m6CGnRqm1o7uV43PL729Idrd368psVufWT9XqufV6zz/5xRp+7lv13c9+qR59/C01GY5qaTzo/slxd+R3XNz6P6oB+w7QG7vjX2fYIS/xIX4kH/rxOT7hTTGWXBwC3Q07Q0Y+8U0fAzyUWLHdfIr+IsJHNlcisTmY6uigX5tMcnAUPjx+OtsrZMXIuBLs1kZj8Mn18SMX/mDAxa8Y028pibRapgAAIABJREFUcu04PZFXJ77xkbw2G+Caj13mgkUWpU677XcMN/lybFcujO8XNkiAwrEU42kzXMmmpA5/fDBvDFk8yA6e3R2WAOHTDq+2MXOZJ5v5tp2zGn7YijbKXCvXTewnBnb8yXi/No9iI8yUvQcRq05snKq19bO15cvq5UHVPefrXR/+2Xrm+z+oZ7/zvVp1Ar+2U26aGW9v1e5sp/u5y2u7WzXeP1OzsbUzPqgXFblrbcvZKvKtf2nfah0dsa+1NVhiok1v1kTkFtlvLnlqD355RDBD8SnrVf6OIvKuDFwl5GoiOC02HH7FB9gO5PjS8saf6DbXFuMtv36Oj+iIrD5/WorOjLE7cdLGH57obXHbsWDcSv1aa25FsscrsQxmLIqjSWCcaGsy7YHcBjuOpSaHP5eA+gKRce0+RTYBC4/xPmWh9Mf1M5faWIsVPanNtzq02Yn4K06JVTduzrT7gWpYW+WfBKrqrrNVb7hQa/edr2997omqF17tHgmY7+50f1OyPlzufvJybf/Kj57EFH4/J50Bh7zELjJsir2tndrIHL7ockke3w+rxSvYwQl27A6u2hz+1IeYfX04smyxRuhTYJuLfgIwjauDH/7DahgpZNJu+a8b0zQyn7VNb0g7fXhtTFsd5kJZg+Rgm1Oj1ME01vKH97Bck8OvPggjNtxsfWxvixhlI7FLawuUSzCOIG8D+uQMY7y9ZO7zpA+Lw3gVH1AlcHgSEGMZZ48zR2rj+DJPjr0oVx/tWAKcM1tqPDDNBxtOsDrAfZvowqMg/hrjOx+6uMzdCEdgb4/xq3XD+WjvAcd3v6nufe/b6+tPfLnGL16t5fds1GTrcq2eO9/hXZvt1PJwrdbXVrsnssWJnfCRWLX+doMHvLDjNTbt88CLfBsPvCmdDwdgtkPxmW1sQomFNj3IPN74QGd86RgOeRF7fLC1ySMfmMf+5CA+xX515g6Bv26TnOGHz7Zga6cfrNihH7ta/rTVWTutTXTQRz7YcNKPrfjI98f1FUQH7NTRk1zgCW/41bDbcWM3S8e2uTAgQWoNSlCy+4aPgTaeFJsRgnEQCR6MfHCVzQuvcYXeED14nMVS6MKjzgGBR4DJ081eZ43gZoyccXYYg6kdHebYlk3PWSS+Jgb65PCSU+hdGvrbkaq5EIz8w6L/dJ1VLQ2r7j1d973/nfXEpz5d3//zz9Wbfv6xGvpXR2er4bwmO7s1WncFc+MtXIutzXY2LKLIqPGyn1zkyWonVnxI3LX5tojg4Uf44aj7BwUdiat5/fAvwo+tcivG+Sq6i+/+CQSWjSV47Voyt4iCj0+Bmxybg6kOWSOxJTkX15aHPD7FuPnWZ1gwbATGxUUfb2Ifnlyx4Y3P8NhqDOEJVvyIDWr8Smwi0+rpQG7h5dg2F05znpEh7ZwlGI1Sa3PCoiSn9KnlhYUXnqLdzpOH15IxwVRsJtmljedgiN4k13iS0Y7B1Y8Ocoox2JHTR22CtCVJzWa8kTU2m81r6H6V3XGdXGbbRs2XxlWzSQ3Ob9SZD72vzt93b33lr75Qr//eP63RO98okN2jBmfWT3T/L60/t+nsn4HEiE66orObPOQFP5vwIzKJbyuvzWZ+JhfkjiL5i0ziEJnoMq4gdqSQi12R6dfBl+PkAE+rK3qMx6foOMoHByMs2ImT+AbTWGyPbdZFu/5aH8jBigz7tfEYb31oecUc4Qu/jZSe+B7fYod+S8EPRvDUeGOTvnbbb3GOah+9Ko5C2J+PoXZYXze2uySnGRgnE7h8lUnG/QCh8KXOeA4YSfW1ZubVChsyJtna0eH+GEkw5kwi8drZ2dUSTM484odxuMb5lORqBwN2bMILJ4sxNunjx4vIR4+falhfXa9XLroNe61WT63VtelWjTev1gl/47qxWm9537vrL//oT+qZP/98PfTwAzVeGdfLk606c/bu2tzequFsVKvLe2c4sbbZ0yFOWbid4kNe8JARL3HRdhWmn8UY/+Fr80nu8MaXQ+C7YTL05F4lcoknnXDNWy/iSXew9ReReVjxQ+7EG4YcJCYOQraqYbNJwb+I8IoDWfxqBSXHasQXvPEBv0cAzIeXnfgypk8m9qjpFCsxVsQltusjfuC1PvHCM5e1mTZbtJM7MrDYQDeKTXjgIHLyfDt0bJsLxxFjJVSyBEuAsoBivHHEWXyCIhiRTw0rbc56/4zfsxeemYEtEPjCGx3sIYPfXbo2L/piH5u0BU6CMkcONsITHdoSom4XKj7PwEiCZLFRO3JsoIddWewWgmd/3BgmFuPJrIZLK7V7+WrdM1iraxuj+uHwas0H07owX6kzl7br9Bsv1On7764n/uhT9dA73lrPPrRezw536+yVq7V9ZasGQzfl7eleXlrqYiQPp06erN3mg/bOsQNe+C+ubIyvNhc+sZcfySWb2Y8/xZ2oi0hc8QYLL536SIySyxwYnt/Bk41gEb74unHTnaT0sJEfYpD1xv4cjHyTe7lTW4OLCA8f8PGdnLZcJ8fsz/qLXzYVNvHJfHwkx2e2kUdk6IGvZitZfrCdfv7AMk/OeuOv9Q0TPt7EMHLwxdJdxfDZZf1FZ+xWw41PMOm6HTq2zSXKOSdgSa6ao4xleGs8Z7Oo3MEYMobUaXNQMOC7m1JQBR3BpgdvkiYRsYGMRAksHu0kPwuulbMhIfzm41M2F/rYboHyR1vtFnI2auNFZOnEwyZ6FfYnuf4mxN+HDNdW6/xkVLs1qVOrVcunNmppPqxr8xfr5EOvq7c99lg98XufqJ0nn6kzb31XTU6fqJXhqNbXVmq8vVTrqydrPpvUio3K32wMhnXy5EaNJ+Punxo9QI2G82EN5oOu+B9rtLm92S3c2CS2iZM2n8Ui9uOLD/LB50UkF64cYeFPTOBpK3SorRdEB530kF1E4SMDP2tC/LNO8MCWB7mTE9gpR+GTg0eHQod12eoQB4VfsQFu7ljXDo82HoUt7Mw6T2z1YfGf7SnGxRSfdco2t/Ija0/uxDI5w2+Nx/a0YdMNi11k+MMmhI9s+86im7iJl2PdXBjCsDyvIFgJGltiPEeQnR+/cc85xCm1wlGk5iw+jgqw500Eps+HB5lL22bhwJcEutkkGUjw06ZHsbOj2EQHLP7xSQ1DAtkD37xFbZNkKx4U++IzPsn/wQ9+0NmEfzLZ3fuvZ2eI8d5DjGdWh3VtOK+LNan1Mxu19fJWvfUDH6in//Av6odPfLVe/988XivnRjVaWa3N8bRODV/X/VhVuVoeVI03r9VgOq27z52t0epy7das+7bb5KCGtTxbqpFQMXNQ9cNnftAdcOxpn7Np48MnfoiRqwpxUyx8i/YockWI98KFCx2GWMCDK2ZiFR3mnKUV2GK7iMjjVTuQ40Nrf9ainFkf8pAzuGd/FhFccq5YHGjWuPWEkuPUGeMLP6wPceU7vcbFUBvBhY+8jfWsEB/g2zzEOLa7krTu4Cp0wsFnvWqHFx6eYCcW7Dcem/Bl7WvjV4zBYt/TTz9t6pZoz6NbEvn/jlngUOrb1Rx5ddq3itXKte0W53bx97x0lE+7b4D2/lXNz+sOyq+/jAejmm6sV919vt72+Pvr29/+Vr38mc/X+mCl+42X9eX1ylVJtx/7gbv9H7kbdQN7f1a/99+Mez9cF/7O/v2rl9aXO+3jjcBha4aWRXN9K/q8R605G8TNUB83Mkfhh++g+idmc2mdaB1t2wc50I71eVvMw/j6Mi1fv93yph0d6bcymWvHDmpfT//+25buW+UuM8M6U6M64YJmMK/5uY268F9+vF6c7dTffvKzVZemNZru/fp/d6uMByDJ+QmGQfs2xbNLg+7KRm3TGth98LqIHNX1zekg+25mLL4eVt8MxiKew3Azvkj2ZuaCc1h9Mxg3yxMdN8uPj0xL/X47d7vt2BXs1LeL9xO3uRzk0EFjfYfxtKWdP2y85Vm0w5trbWjbwejraPsH8Ufuem3x+AuSrgxr6k/sa1AnJ1Ubk0Fdnu3W5mhc9TPvrEfe91P1wte/W7Ovfq/7Dd0lv0w3mJXHjmwus/1N5voGc30fGZYL8bwXdvXS/Zea+rVr97pZx9VYFN/j0vGTjJP1wMb+euj3F/nR8gazHVsku2guWH2ew8b7fAf1f2I2lxj3owaqDUa/fZCOW9HX8qbd6gi+OvP9dsuTtgPb259Z97u4e38B62rGRcXSZFCj6aAmS8N6YbRbdXZU7/qlj9Tg6k699Ad/WnV1ViM8873PVCbDWffLdNOu3tcAbOYBx+4xx+4qxhUMvRP/PDvae6sUe26nThwOq28Hs5U5DDfjLe/ttINzWH07mH0Z2KG2nbFFdZ8/di6SuZ2548T9idlcjtOpNqgtrjZK3edr+207/G3db+tnLLL9fsYPqvc/cdn7NwA22ly6TcGjAcOqteXa3Viu+cq8zr3nbfXAQw/Wt7701Zo/9ZL3TLXkk34fzA2nNR1Ou7dF+h11Ez7S2b+02Z9Q0euLxtd8BhO5Y6xvJRbHqPYnBqr1X7vfP8rQ8KcOfx8r47daB+c48X9iNpdbDcZh/AlSf37ReJ/3dvttYg5rH4TtwPYJycyHIK5e5qO9P7P3Hsf7ltGgNsc7tX7mdPdlUJ07U+/4yIdrez6pK//Pp6o25zX0jYNfdhm4cpnu7yPXt5e93UN3T1G3eeXLIhvM9bdQBxl4Z+xYItCuiRbwsPGW56B25FIfxPOjjsG+Xfxj31z6hvT7BzkbB46bN7oW4R70WUDsifxR9a3yw8vXg3vYo/JEkYP8+sew3eXE/oeto2Fd29qp1aWV8kmMZ47O/9x7a+XCPfXVv/h81bOXu39oXKpJ9+2Rf3D0GYzPb6aj/UvxZmPproT2953rV0z7V3T9WPX7iUV8Tp3xw2pxzlech/H8qOOx5TCbf1T8vvxBa6fPox+7bob/KNsPmz9svLUHT2tD246dLf+P2s5nez8qzvV7FSwg3+P7Tj3O+K68dd484pxx9zr4Ln0R4YONN/cHwAlusNQK3rTxKL7bR7k/QLu1LTaQzZyaPvJ423Z0uA/B/QcovkVH7DOeexDMuVcHwfQ7l9PZ3h/Kj6ZVy9NhDYXI/SrDWV0bTOqu8+frygsX6577lmu+NKr52x+p8+9/W/3w3/1xTT/12Rrd/0u1vEFuXlvzcU09l7Tir2PdRzKroftfuN99S+Q+i6rxUu1dCe0fAGLLXrayUb/1KfExxnf+tPHomA95cQ9KbgTjM3k6Qmm3tbYij12cwnxAnZy7Dyk+YOMLuzNGL6z0bxYfPx2IDNz4kTjFLHz4E6+sE/zsQ3jgILxK2urMq+lC0dvakjjCjQy+tuDXb3035hh1fwx8spHHF5vNRX9nxC28HNvmIsAcsIjcBORGHTf7uFHJnEVoHunHUTcNcfKo28clyl2VbrxzU5JbnpPcYCYR9GTRs8ONUsgYvWyyIQha2vDJsS38/MBDRvJsIOSSmNwF6RZtOMbxkIlt8BB8Bxdf6SHDZ/7747PJyt4CWJkMan06qJPjpe6X/V9cmda1mtZ4c7eWhuPaWr1So+Gstkfjml24qzbOnK5nv/iVuveDb67l1Ufq0uVLNTp1slZXRvXyxYv14qWXa7A9rfXZUi3P7C3D7sJla1S1vVy1tbR3wEx3dztbPCohxuwUb/nMAcEHPiOxyWMV8oFvEZElI342VrESIzlBYmJM7PDo4xdXN9CpFxE5WGwhJ+/wyIm7taENm638IIOP3FHrLxuDfJFP7uggnzzDzDpiL3wy+PGJJRk8CorfMMSdjDWnthYTD/JyE9vxiCUebfnCYw3SwxZxTx7h0wVXESdyYoaHPeKEx3iOJzi3Q8e2uSRIDBQgydDmKKe0GclgfYXjAq9kAR/mBHmLTCAs6iw8QUghSy898OgIPx0w8LLPfLvgyJhLsmBJgAVJTsDJSTQ+evDCcLcqwsdfc3jpl+zohGUcxYfuYB26UW5P3lc4q9NBnR6Pajyc10srs9qej6suvVqj4VJtLq/Wtfl2vboxrdVHXldnHnmgvvC5L9Z7Pvtwvf7sal186flavut8vTqf1LMvPFdnzt9Vk8tbtTFbqpXpsEYz/wRZtTOa1fZS1TU7jiuR7WlnkwOR3Wy14NTJTTYXsWC/RZ0iH4tIrPKcDFwYsMUGiaMxtRirYYuXPNC3iOCQw0dPsNgsH+r4IkdsiA7+4VlE5MWGrDXFJvbJOXl5RtaRseQdH35rxFhiSTc+FFvNkYdrLGuEnHE1LGuGPH5t/IklHm05JMMvvqrFx3hsIitu9MgPe+DSbVwbhnI7dOybCyNtAhxhPEcTVMYqMdwcxwTp/vvvX2h/Fg9cf2eBn9MC0ZIAKYKYBGlbGP6qwZiFwia2CDr9kdG2gBAd5hPc8LIlbRiIvNup3aquHdvwZl6SYZNxMPobD5elw8GwppNp9/tzu8NBDeeDOjkddT+8vTraw7p8bV53nz5Zd7/urroy26r56k49cs+DVb+8W9//1nfr4tPP1JtWT9Ub7xvV1om12tm+WqfPn6sLDz1UO1d3up/I9FfTS91ddlW7S7Mad1cvfom3auvilRqMp12M5FCM2JtNkj/GzCELWjwVt53L9SIiZ4MX9/YvMOQjOVSLTXJDJ/3idBQl39YGe+gTe/JsC5ZxY2pj8pjb7BfpiF2uHFy5WBvyDYMehf1yj9iDrDv+8MHayji88CYG+NhjjXh8QWzZbjxr1pwx8nQ6Hjyuwh/84aWHbckZXebIsAOGOPHdmjWHBy578MVGODakW6Vj21ziPCc9F5FnIown8DGO8UiSJNomY1EsIjKc5aRA0BEc4wlKxmBl8djtE8jghC9yApuACjziA752LnLGgsV+i06SLIrwxB86kHGJtYAcuDbhzo/uw5W9D2+3R3tfDUuMcsZanczrO/Nn6/TpMzU8c7JODjZqPrtao8Fy1ePvrvs++7Z66jvfrvc//1KN3vamOrmxVMvPbtW582drNFqvk2c26oSPgn2spcyr1jyxuOQel737Y565snc2Zw/bEhcHR2xPjs3xFZ988+mo/MHA3+ZOX0zEPRS9arm2RuQhOQnfQbW4wsfrwIfd5on9Dsbk0/pgw83YD4u8gxs/OQWxNZj4Qsatbzod+NkA23ntyIQ/2PwgkzWjTg7I4UdywF8bRTavFjPtyOS4k2v5pSdrvwPs2UTPt7/97UzddH2sm0ucYGicTEA5ZFzyjTHYYhB8RXIWERl8DmJnQG1BRWQT9NigNubAtyDUFhMbjGeRsSFtWOyiI7hwsnDISTAiB0sd/PgR/4JBHg7f2UFGnbanmLuDfjqr6eqgtro/r6+ydE+5iNqe1mxzp3a7b4Hcbjeotcn+bbd3n6oLH3xPfeHTf1Yv/cmf1b0PPVC1dqKu+R2Q5WHtlM+S5jUarNaGtSjM6m5h6vhWqbpftGM/28RVHPjBNyRG4scPNdvNyYU6ueiYD3iBixemNjzxTFzUyBgeNVzF2sG/iNjLptjDRvFWIzlQ0pa7+EBf5jqGA17wtOuPPjar6Yg+uPGFn+xnkzZeNpmnT79P4U+8ycUPdWunGOmTSbExGbNO4ePRThzgiadCxgkumPgV9sUHczBuh45tcxF8FGM4YYxTAp5dvjWS0xZlduh2rt/mNF7ByNsuYwh+u7gTIGPOsALJFslBqcmxQSDNJ6DBik8Zxx8ip2/OQtDmY2TCp9/K8ZX+nDHg1HS+d/+9zdft+/aT/SuXDme+VGdOnqqVE+t1eTav9eGozow2qnZ2q9aHdeEjP1Nv/L/eWN/866/Uvb/ysaozb6o1B/Haam3NturU8Gy3IflZ3u6RI2FzLA8HtTRy1251v8G7u7N3FcKn+NzmLb6p+dGW1sf43tZkxEnd+dz8k0N04RcbfTzw5VId3S1m28bHVvnGzx5jwcOrj4Ilz3hdGWWsxey34Vt73sqzMXh0KCHjrQ9yzZ+Wpx+vyLBHYRub1LCMocQOf3yDL7aJb3whFz0Z04+OYJrDexDhP2zuIP527MbR0o7eRpujjOS0DSW7IcNa44yb7++gR6nEn92XDv2M5YohurOj44+MsbRT0xk7YYWC3fbJtDyRw0NvdLf+RSdZZwnUjsFz9qyZp6Ed7HvHvGsj5+lmuXYf6l7b3anNa1e7Z47caDe7slk1Wq669+56/Qd/ur774nN15evfoqQ2fPXrT9SubdZovlPbNev+U7ozYv/zOT+LOdl/bGBrZ+9sZiNml5gifoUSN2N44ksbi/D2azww+RscfeX/Ze/Omi07rvvArzPcqW4VqgrzXABIEAAJgDMpSqQk0hptWS2rNTjc0e3ox44OvzrCb/4E8qP7pR9aDx0Kd7dtSQ5TsmjBlElRJDjPEwgSIDESQw13PFPHb5/7RyUO71AFXloUzXUjb2auXPPKnXuffXLv0+qILDRo6VGOgtaWxDs1+Up8ig3q8B0lnyy05LBRSQy044M2WoW+yA9Pqyd2wYUnMvEBMiJT3zzCF3vCF/1o0lbHZnTk6KckrtHV8mqD/ezeGzqyOrbFxQLCGcZY7bJK62cCGTdmEbICZzWHM3ZYiTyBECg8Vmp4BS+IfPYkmBKSIMWGRCb4yIcPLjTG2Ky0ELrUdEZ/eNDTmTMOGeiSbPS+iu5Wk8Gse0bID8J6dVb3id4qszapF6ebtb27U7eeOFsnrEKzfvWvvX6+DA1P1Bt+45erd+62+sv/+MGqF87XTbNeXbtxsW5bOVG93Qt1sTaq+7JYmByr9tBMduv8+FLt2r43uLxvhe2JB98AexPj5BpOG62xqylk4k08Ijsx1k+MrkR++GJn5lb8iD412ujln4PsKNvZGlp1O/8yRja8Akem+ZoFIj6i0yYnRZ9N7IYLrX7G8AGy+WWMrshQg/Cii5/dQPPPWCBtfCkZ+2HqyyfHH0bKHm+c4XCSmjoORE1oBcgicRSQGTCBlAROLbDRkToJaBchY62syCAv+FwuRh/ZxtAG0lbTE/2SQ0cK+tBqwyf54e2ehO4mhYuXXi3vyUA/G8xqttqv/tr8FxpXex457NVsOJfjmyYwvOPOevDND9c3/vQ/1e5//FD177qxzpxZr/ETT9c1d9xe01rtbrXM77l42UuvlpZXarn7TqpqsLeA8rO1cb/JFvvRKul3hhzwD10u8bWBmq79QGzkzbg5chSQlXjKR2Le6oiu6EdzNfMv8iObTZGZGi7y2/mHJ/j40vYXfUxM8bWyW93RD0eXElx0hD518qmO/vAt8qYf3si80vrYFpcY7SBzoFqtHaT6gCNoBErRziKhDt1BhnMwdGpnG3KSlOhPTV8rH71CjrOJiUsnOzOJoxtfC/REJ1qy8UkKWYqrI5fZPv8aJ1sdX7VB6I3HVvi2j0cB8cG4Nn569QEZPe1Zv975lrfX5h//ZT3x5x+utXM31ubqoE7cdGvd+Lu/U6fPLdeuj1Cutkf+7R2wvqLsz2ra7Aehg1yxoic+xMbYJJ78Tiw6gw74Rx6+5DGy1YBs7c6fvXiHh/zQHSC+s7GNibaY05nYhze64oc6vKHZr0bDJgWknfgEjw6ulc8HeLkLfXTq5wCPLRnTN0Y2uuCjK3bKmXzEZ8cFXvh2fuOPXZFFhnbrD10gtNFzNfWxLS6Mi0GtAe2kaMe1BSKlpWv50+Y4GguWG2tqvORkLLRwrXx8zpoCDg/U8BJ3lO6M00MngFPIkTxjdGSSwLe6jEcnej5koWrlhq5T0pwZyY2/5KTd0ZnrFsT103VLb7km3/pePfedJ+ul2W7NTp2uzc1pvf5/+59r5cbVqmGvamWp+1jkQcmV3lINalBDv0PdfPxjB2hjFttCF5vgE6PYvVhnYQ+vce3EKHFNnzzj7UK3KLPtswE9e5XY08bJOIgutYI29K3Mth3f5UwJsFdp+aOzlU+30tLFV3XkozE3nKRAaKKPzBaMsyfzO7rR0BW5qclH285VY5EbuuhY1B/8ldTHtrhQFscsNFZqfcYuQgw2cbJ6oj8MjAtIAqE2YdXkCCR9WYFNsLTJ1UYP8FiRgVpfAWRkAqCPfWzWTn+xbVyJTZ2w5l/sd3WDjj4y9NWSfhAYDw85bIZjK+jb4by5VZOvfb3Gz79QN4yqVkZbdWZ1uV7evFhf/vcfrFt+8edqeXm9lvrr3WMFk8msRn4vabxb/aVhLe19vCKXDznjacc2OO3Y3uneW+CPyl/ijYfP5OBJ3siWs+Qi+UBv7Cj57MbDXoUOsl1Z5Qoa3oFIlrlEbvQcJT/2k4FWHZw8aKtjP92tfG0Qnq7T/DOOP3TkaNsWkXkvZpk/9AMx0+Z/chefjMceNuNvbSQfrxjRcRCQ+1rg4Bl9ldIYzQjO236tCLBvHzjl4ADoBETNMRulBPA73/nOoRolxYqO3lbqZ555pgs+nYKU5NKjCBb9NtDZDcsetgA2mmRJBloBZqevMu0+BfTgJ59ufGwnPxOUjPy0CNt8VcmWTFZ+AnQmORnsIpvMTEK60ZgM5IePLPrZD/AD+NRrG5fq5he/Xxe/+dXa3tmqU+tna7Z9qZbGszo5XKtLu7P6xqOfqjMrw7r++nN1YTKqF4fjGk13a300rtPra3X+wqV68aWXOpvEhh5xsUeDLckXnDafE1dfzSqHAT70eLOIiLk+fxNjMQDiIg/iKCZ5afpBOiLHS8DlQKzJkHNtusw3VwRqXz+LoWfU6OTnYZCc8NPcoye5oAe/GrBFDAEf+P2tb32rm1+ZP3TGV7JT4MSW3+R5Jon9YkAmf8SSD8AYe8wPPOaRmh7+KeYZPvzGyURPFzyfyNQ/aP51yq7y37EtLoxKYSSn1IIgcJzVV0wkCTCWIiBHAZl48UisfnTSAcgH6KIfvUTBoY+ujGdi6hvLuBqO7NiJX98YPn1y9dkUP+HQZcJps5ccMmNfZOAny1js4Ud8Ro+31Utm52u/6rwHEG9gsXeKAAAgAElEQVRYr0trVS9NNuevsdveqllN6+Zzt9SODXjTcW1OtrvFZXNQ3WMHvUnVZGtco925D+STS5eJSL9+bGMHn9gJF/vwHQZk4CVTjVcBaavJVYAabWzqkAf8I1fcws+u8O/nA7lK8ppYHiC+85nfsZFMvIlNavzk6iuRz4f4CR870etbJBLL1rbYTg79oYlufXLDo01X5BsXG5B4xCY8cCD26e83/zqiq/x3rIsL5wXJNmQrobMEZ+FahwUTPqupFfXuu+9+xXTjiyAgDlyy8lxLGwhjQDDhMxHYAfwUhC3Y9GYR0CYXDfoE2NUKQM8W9pFpHB2cNlvIcBZ0ZuS3syYcOySppdd2hjPuas0zNnRnAsC3PrHBWCarLd62bJssZClgMNqs4eCOGg+n9dL/88f1rWfP1903XFu1MaoLz13s3v/ypre/rXr33Vt1+vpaGY/r9NqwVnr9uvbSTvfK7vHTT3Y/P+InW5zp2JK8iW18jk6580iFuLY/s9EZtM8/8eE7fz2XQx5fxRbwM/rkxLi+OIkpHYdBYuSs7GdC6CGD3lwhyjt9bDeuzyZxlevDgE18N/fYSgc5dMDLNeCT8Sx0ciWW5jfdaOM7fAAdH9irZpP5YW7xHx6/mu3mH+Abm9CIK/n8il62oMEXG9VkoffYhhjIMXsU9ikAP3s+97nPdf2r+XdsiwunGKIw3McLBksKgAMxXpsDHONsJkPrWMew90+AJM44en0B1G9l0g/YA0wA9PqKtoIXsDHtJCR9iyP5AXi8gKwkhM7I5AeIrfi1TRIgDpLfTg7JI48fIDq0M0YHfRaXlraTv9KrUV2spXc8WG/+X363nvwPH6oX/ETpBQfatXXuf/gHVW95sNtLM1vq13B5biNtvZXV7tmlleE8Dg5oOgLks5kdJjBgO1vYJL/JXXj2q9F8+9vf7obI4au48IWcyKArufaRBZ25BHcUyDVZZCbecpa5xxd2G08u0z9KvnExCODLPCE3czA5hGOLj8qJIRnJHbrkOXOFnfAp+mKljr346Zan8KnpQhOb0ABj9IiHvJHFHpD5bQxNa3tH0Dzmkv7V1Me2uFyN0r8N2gTub0P3j1qnp42en07qhtUTddfv/1adu+O2euoTj9YzGxdrPDxV9XPvmu8AXh7MX3/pjPQqoy4voK9C/7Tzdz4CxzHvX6uM+Wn473wI//t2wCsy+/1r6gUv4z19qnrvfVfd8v6fq+vf89b6/kqvtp/8zvzH1paX5hvwXEG2IXtVpx34afunEXjtEfiJXlyuZMW9EprXHt7/Vpz9WqrVOn9xp6q/XOVjz7lb66a3vbnO92f1uT/991UXLnU/auQXBVynuGjukv/faGH5yYjzf6t8/mTo+YleXH4yUnS0F8Pqda9TuG7giaQT3QJz0c3Sm26sG+65px77zndr5/Enq9wDnFQtz1/l0i0y3W7dn34qOjrIP6W46gj8RC8uuXF1WFSuhOYw/h+HseG0am1cdX3faxj83OKwNia9Wr3u2nrje362lpdX60uf/lzNXny52/6/PJo/cd0lf/zquy8/Kn9+EuL8o4rNT6rcn+jF5Sc1aT/gl/XB/kBfzL3oFQ7DmvYGNR0s1cqb39J95fjFv/lU7TzxdPfN0GB33L3Owfdp071v135A5k8RP43ADxmBH8ni4vP1UZ+xW5qrOauhVVp+MWj1ZczXcCA8R8UqfKFb7Ae/WOcrRfjwqPcDNhm7Gp/JOZSeKht3fbw5sVa1ulYX+/16Ymuj6rYb6txb31KXvv5Ejb7ynaqNS1XT3Vr2sckWu+Gse/J62r+8tyE+LNq/iE9cD/K15c9Xou1Xnu14KyN6Ir+lO6jd5hpNK2+Rpx27Gh3ktPSx8yB90dPytLZkvMXtp2NxXL/VfZD8RT50rc62vUh7HP1j/So63+HbsJO279/thcgB2DqEzjins+/jMKfIyOTES5bv7YE9CL7jJyt7a0w4ctkCgkebPQvhM54Dn00gm6Rie0tLVujIR2v/SuwyBh9etmrbFEaPMTT4QOwxFh54/XaMP8YTx27CeOXl8t4CNJvUbDqr0TUnanN2Te2Mz9etP/8z9bo/+k/1rf/wSN3/jvtr+Q131O5L36+l1RM1W/ZC8ovdz7mSFZvotPdEnw3G2MpuupMvfXuV1IeB2MgVusSV7OzLMG7vBhDb6ERPV+J0kA5xJ0ts8MZWctmr8MlYcORGz1Hy6SU7sSeDTn17SsjO3hK09MUPdqUPl/HoFltFP/MHPR1iq20svmmTI372zrS8bOCXMXxKbFbzEz882XLMdmMgerrOwvwL7krrY11cOMTgPLsgqDYRcSQTRyAyCQTBblgHHAcPA07b7CM4NlfRIfiCTA4dAmsyaqvpQm8Ho+cv7CgFEmiiJ0k5iARYssgHbE4yyKOP7eTSiQ94FsQ4ufzlS2xKYuFsBlOTQUcmBh9id5JLBxBTPJ7/4FfsySTt5E+mNRvb7Obt8Ts1Xe/Xty48U7tbF+uGyVLdsrFVD7zl4frSpz9bvQ/9l3rj6V+rZ194oTamozpx5my9fOFi9xU1m9iRCcr/LBzx2RidTz75ZD311FNdXD0nJcaHgQ1bcsB3/vBTjOKn2IoPH40BseSnse9973uHie9iyS42iSs7Afv5QS5ZxtTsEVs2sYMPhwG7FfP1u9/9brezVS7I5QOf6NSGYwswt8WGDvzB081P9HCp8ciDcbi82Z8utouFmj7j2k888UR3bMDJH1q1vsJ/+tGa954ryrNq7HMswSf2sYctmX+dM1f571gXF7o55aATaLUAgARVPxM0AeBAuyt0Px8ER5AkRG1y4DdRJE1g2uQl0WThRWtxol8gjeMxxs7QkJ1Fgw52sw9P+MhAn4SYwABvbKSPfLRqMiRXzc7QJh508i08iRf6TBL8kW9cocePKE53ZjVcGdRs0q/pSr9Oba1191euO3G6Tlx3ou78hx+oj3z983Xho4/Wwx/4xTpz+pp68aXn6/Zrz3b2bGzOnx7OBCSXTezpdOxtc+czvbEfvTgdBWQpfMcD4kPa8FlYxEVu0cgbOw4DsgG7tNmZ2GcsutVsFlc6jeM7DNiFLwuThZBt8gPo0kcX2uinJzurMy9CFz40xgB7FDYq5irdcLGdXvrg2CJGauMKWWSap3wLP3onQX4rxqKHTQfNPwvW1cKxLi6cZayf17BtmdEJAsMDCbqD0iRQ2meLQtfW+AUsT+PSQV+bLH3BUbTxOOPT59mUXLmwKYk0WbLQxEZPsYL8Xg5ZZITWWNp4JMkZjQ52AToycXJgSDCfjZlsnuMRJ3gQ2/EpkYNe8RyIZ07iGx862xx3k173FdDF6bjGPRN1Vv2NjTpz4y1VpyZVt91Wt/3N2+ubj3y8dh97qq7/jffW0k1n6/Q1Z+q666+vp777dKfPMzbJm7zwk574z1Z2OuOxn01KYtUJ2eefSe5KRKw900JOFnSyHQj08ROo0TgQyBenw4AswCa2ONDY7UzvgAJ8oQOt2ph8yNlR9uNlpzM+28QJTv7h+aU2Fpw6Vwh33XVXZ498gcVcp88eceKv+ap2TJHb+qOPB84xwV828ZVd7KEfnba6tQ9vng3Dl7zCo1MAPsVT4FcLx7q4UB7DYhwcgxPUFq+dABxluCCSE3q1oJELbzy61LHDmImLXrvVv6gzOgQTdAfuwk2wloc8hWxy0ceO1KFHB+Alnw58i3SL9sUPB0LObos8c7/mmnpdHKa1NO7V0q7fDBl0O+Zmq1X3//r76tmPfK4ef+Rjdd8H3l6nr72mZpPdmtWwxtN5jOJH7DDp0s4BRBMc+5UrAfTsV2cukBdZDnaQmGuTLU6JXUdwwD98rT2R42Br7cfOpwAedh0F7EPLFvRqOhIffUVukh+2o83HJzrQxB512sbIw4tPAYlLZIZeTRY6iyU92mwMDXmBxMP4Il1kow1v+PQXcRk7qr4c5aMor3CcIRyJYwl62DPOybYkmKFbrPGRJYjaAqKfYEUfOcbblRhNEpDkqVtefO2koz+20xm++BY9xnLWDA/9GdeOflc4ZMbW4B0A6AGccXytf+3kYUsA32Q0ruX+SveahV3vxJ1Mq7ZH1duZVmkv+9H5ad305gfq9Q/cX9/80lfq7s9/tZZ/9s01nexUb5WN84lJfwo7LITRR5fJrmaPgpadsT92LdaJCXx8JBtYZODQkCkP+pGP5krkxw5yFXG1KGdRDI7c6KRHOUo+m/CRp6CnD4iTseQ1+TMWP4yDxFIbP5/DnznbEe79Y3PmZeagofC1MqLXGIju5AweLnTagI7Y1Y6TrX9UbDoh+/w7tsWFEYyP021A6E0Q4jhn0CicDf0+NnYo/Ao+JRMmshMc/QQvOiKfDvpzNoDXVodPHVnB6yvxDU17RiSXbehb/zqhe/8ii90gfkfXYh3e6KavtbUd76aS1+h2n4wG1R/MarW35HqEoqrhtC7NJnXtNet1/3vfVd/64lfqm3/18Xrjg/fV4NrlmvkJ2cF8QWZXfKVDO7a3OmMX+jYXodmvJkfBC1KLWdpqNMFpk0/PlQD+FPTR2eaOLP3IRX8l8mN7+GKP3MMB7QC58PIWHnr3g/iMrrVfu7VdH8Ap0U2H0tLGXvRtHPiaYmxRX6dg71871uKvpH35uulKqA+hyQpnlbNK52yunVWd4y20PC1+v3aChicyQ5eA6wtiQODZgyfFmHYgq3Irg+2xH13GQgunTX7kLtoU+Wq2Z/KiR+tsod3ai7adnPpo6CIjbbUS6LuK2/sxNYfg0Ftxp/3uNZY1Qzerld5KVa9fJ958fw1uPF2PP/rZmnz5sardnfJr0eO9vEVucqVOSRxau9jWxiU2LdbJRUtL7qL/0buoY1Hefv3EpY0h+ZEZ+9OP7a1N+8mNLeTjjRz4+BW+tk+uvhLbQrdYRyY6c0MB7FfggbkTiFxXUtt7L4gPDo126MlI39wmP2N0GwP0pK3Ph9B1BFfx7/KReBVM+5EykAOgNQ7eagzX4pNYOAnL+EF1EmV1dhanKzh1goI/fTXZOWvEvv3sxxfAowRam4LLOP8UEFxoWr42QRYaPqgzafDEhtSRSW6Li/zUxnZ9Hc2G2bSGLlj6fgtpWLOVpZr2hzX0w2vTWdXdN9Rb/8EHavryxXrhLz9q+la/pt3+u8Sz1QUXaPFiqbBt0e/QtzWa0AfP98hvZRs3FtmLY+FvazTki6k6vrTyIyf1Ij/8QYUc9sh1/IVjJ1xk0q0P7wBu+YwFWj3BqdHnKlU/i0xocpIKP5noM8cTZ/RtO7LJb22EZ2tOptoWq/hj3i7aEFuOqq/sWvMoKc2BkYOfs4CxCmM5FYe1FWCM04eBhKFxN90NMjKjA5+AoIkOehR0+LJaRw47kyC18VxWJoGxzRhc6MkVdLIEnu7WH3ytP2yIr/hiCxoyW/rQ0mEs9ocWnix4Bc2k+w1pP8var5Xq12wyqUvbO3VxZ6uurWkNfa3sdQyuYvz867veVN/747+sxz/7hbrx0mb1lk7USrN/hy6Fz3SA6OJz7Irtrf0d8T7/8LFdISt5IAMuEH3wGTPOnqNALpzB1ZkHiRVZyRlZyQeZ2kfJRyNv5h8d4VOTjT8+xu7oiG41HH+0+RqaxJUc9itoAuaY+Rk7jaWgZZtCHrmODXXiGftiY/rks0ds8BgH0QfH59cCx7a4CDgj1ZxkrMmZIPk6zbgC1IKFRkDi1EFOoA+NNr4Afv12sTEGr6A3pmgrIHi11R9IGJ6027HIMkZf7CFXsozjx9PSooMH8AocvvgRGmOAjNCnbyz0oevGXH3svUpBXRZiO1uHgxovLc9frTAyMKvZSr+W7r+nbr/3XP3Nhx6phz/3pVp7+5tqZTa3mR1KqycxiQ9si/3q1pbO6H3+meSJWej5n3ZY9MlX0GdBWKQLfVuHF1/sT20sMoKLn2rlMIjPaLT3qyM/48kvfHRlLDFdlMO2lpYMoIZ3HAEykw9t46GJHWrHGLB1wF4YeXCM5vg05mTty4acoOlxPOQkju+1wOUj9LVwNzxZPLJgCBJHOCygWUG1Od06qc3ZwyA8HCfDokWHNt7oEHAleAtdFjh68KNnF2iDrI9W8NMO3WK/1WkMjyIOi7aGV2zIZ4diQSKHTbEbHj/7QWjQ8YWOLIRoOjrb/XdGtba6XLORq4xZjZZ6NZoOa3s26X5ovnZ9LBrXaOibpV7d+I4Ha/jJj9cX/vw/1bvuvqv7xomOTNjEkE5tfhkXDzalxC42HwbkKPjFQCzw8r3lhZNXNCZ7SpuH/fSwMbFT48eDPwds7I8dkS2exg6DzKfkJvrwaCsBbfRsUGIPPH/DE3u7HO4xswOdMSDfDvzwJT7GYvMizyKNOIg32xX7mMhXi4Xd1va62ENlEbIr2L4f4/qtfXtmXlF1bIsLowXFJZRNaGobe6x+rUMJPOs4pi/5nDgMBCNB5qygCyLZgAyyMun1AZzE0GUyAbWAkwnvwEGnkB2Z6OiBM4Y2SUo7eLbAoQcmVWShoYue2KCPh9/G2Rg6+vGCLC78gcNPNjyebtLNqna2dmq2M6rJzqRmq0s1Xup3+1dG27t1kd+7vepPd6s37NXG1matvvtNde/X3llfeOSv6qFff65Wb7q+k8UuNpEvRvFHn144drJdDdRH5S905PMBv5r9/IJPndzEzyuRjyYxIsumRnGUk5yxyZMDPplL+mjBUfazV+6jg4x8XAgu9pPZ5aWTPP9CgHx0wbMXXXKdfNKjbcyxg4+d6BQ6LYaxm01k8VM84bXpSs74jC+Lio19+jbGidPHP/7xjuc3f/M366tf/Wp95CMfqV/+5V+uN7/5zZ0NeRxmz50rro5tcaGRUwLCeEH0TAUnBF0AOAuMCZS+8TZRB1mO325FwcizFPQlOeGTHJCJQL5duiasOklrJ7Dgk8UuCchuRAnCz05tycvikonKLjsk1WwzkdEn0XwH+E0K8ticl1XTiV7NNnLwoNE2pmRCWLD12YsOn+3/NZrW8mBYW+NJ97vS37v0cm2Mdqoms5pd2KiTk2mtzjyMOKznn/l2vf7eu6t/7rp66qvfqG/83/9frf7Wr9Z3XfbsLWjsFG/xZDvb+Mx/OtkvD96C78zn+ZTDwMHsmRyy2A/kPfGB4zNACzz3Qyca8+owYBPb2NTFZO+qTh74QRdZ8qtOntjkAE7OD9LBf3axg7/yYCct2zKX8CaHmX/mhNyp2RXbQoef3/yPHL/hhQdOXMWMzXjZygdzAz2b+GxuGUPDZzV+fGjQs4k+J3/zJyc7dF/4whe6nLpqERv6Pc/lGGbra4FjXVw4aCu1LdgMVzIptDkIOA4EIQvQHXfc0eEO+oeXfE6bKPfcc0/ndA5C4wKXQEiIvgkgmALGLuP4BRqPg4dtOVglDC+47bbbuuSgg2OvcXLRkwFMXglyWUkPHZKKTgH4+W2SATQeeciEMk4PPJ/iF7lsdKD56ZI8XpBFlPz+dFa93VktrSzXjgm1NKjxy8/XljjdcVcNdnZrMB3Xidm0ljZ368zqsE6+/rZ6YHWp+v/58/Xs1x6vB/rLddM1p+p1d91Vs0GvNja2av3kek3H84VV5vg/XBpWv3rde2DO3Xmu7rj99i5OYnsY8I1P/LX9P7EXE21+JlaJq3zz8/bbb+/icph8cUt8z507180V+sw/B5dxOdOWfwco2XjEVf8wiHzzlb1yR04X/+ZemzGFXOCEZk7kkQd4POQpbNSPLcmrPDsmzCnxMJ/MkfhDBz5jFpXoIJ+faMknj8+OgeiSA7bLGT6PraD9V//qX9Wdd95Z//Jf/st63ete181VH4/o+drXvnZYePYdO7bFhROMAA42hRM5GBgP0AgM4GySFbpuYJ9/+PEKnsCZDPiVTMzIJj94Z2B9QXS20ZaQTGC87AR8oCf2mdwSQx+Q4EwaCcSHlg6FTPSAXHyhR8c+8hW0FjV+oI09xtge0GeXp33JwpOJQx7o2YW7O6veylKt+NjR79XaxZdq1uvX+t6DfINBjwNVw906dWqtZtWrwc23130f+EA9+gf/R93yua/WdQ++rk4NqibXrNfw1Ila6g2rdkc17NuIN6jlE2vVt2BOpnVyZa3W+oMazKbV702PfPA0Z9XENLlK7JNDvsLpoxU3fsvdYYBerBIj9NpkKWKWE4K+eHeL5d4XCkfNP/IVfpAlb8kZX+Qs+WAH4IuTib5nyehdzG36aPGzid/yrOaHOjrMY3rJZA9+9mR+x0+6xA6ddk6A7CLPlRpaeLosNHR7juu+++7rjtscw0f92uVBebk8iw+iuEK84HA0wWE4XCCBECQHIloBkSzOCYQSQNcWEwUIlgLIQGNM0Qdw2oIKr08/Pm22GQ9/x7R3dYEnoI02EB34olNt0qrRpkggXIBekMnhDMQmNOQFQpe+OvaLT2x+Vc3H1WH3xu1Zf1bLg16tuWz2WX066XbfkjMbjX3mqFo7Vb2Lvpo+VYN3/0ytvvG++vof/0Xdc363ehvna1w7tdub1nZNa3tLrgY+XVVvMKyZ/TMWrxrU8mjSLVjyZ/Hiy0HFQeJsaX4kL/E7c0MfP38zxufE6SDZ8A640PIVLnVymNjqk6+QnQPb+EEFT2zrBO/piE2RbUyb7JbHiSnzW20uxkft0MYHdsV+OsIb3bE/NfmxPbjYhge/Y82YWDmpA7q//vWv18c+9rH6/d///e4K69/+23/bjaMzt50wIzv6r6S+PKuvhPoQGhOMARJlEqkFKMFKgPS1gYnWBvkQ8T/00GJyfmiBP0YCbPvvdsHN16/quZVrwnaL8OXPyxOL2EAZzh9onC5X3XRjPfDen6uV3VFd/NwXq5aXalDj6tek+ynYk55G7s0furb0d6pmVd2vCExt2vsxCsSPoSl/2/Mu+h1rTmyOUQuL2schJ/o/+qM/6o7Jf/pP/2m9853vrL/+67/uinCis8i8Frh8Wn4t3A0PJxgC1Fbi9C0yDMzqakEBFiRnMQ7+FH40EcjZI5PsFS17C1GdXK+H3/dz9dx//PN69Iufqw+c36ylMz7yzGq7N65pf7myPJHltGAvDZwHrqeQkfWK8J82ftwikCsjdvmo5uRvTriidP/oDW94Q/f18y/8wi90H5F8PAKOW/eNXgsc2+Ji4WCIxcKlF8iCk7GsnhYVC4yCXvlRwA8cUPsouRKafdh+bFGuYhaP9b0l/9U2+7hnx26vX3XPnXXzg/fXX3/4Q/Uzn/9qrd/0vloejqu3slZjG++6paTfLSyuWKwoY29zUPB32/TmOX+1ksu9n7Q4X/bs70bL4pKPWu7/+KLDouHq5fd+7/e6RcZHdWNucOeYtAjhfS1w+Iy4Con5qKNuPxoRwTiTi3PGXNH46MRBC9FRd+qvwoyfki5EoP3YMnC/xBNIVpvlpfnioj+ouuvdD1fv9Mn63Ic/VvXyuOriuJZmfupoUt744lql+zDrVsB0vrDsuvnrl0wWdP60++MZgSwujjdXLD4xOC59XHI8OnZdCLTbCnyEeq3H57EtLrla4YBiQbH65QqFwV/5yle6vQ6cMp670faJ/CggH8sOk30lNIfx/50Y27sv0r1Iyo1CxX0v91/GI1831ck33F13vOn+euzzX63R579eteVmrQ8/s9r16gYrCjl7siwqIzdE965c9tAHhuO/izgf6P2Px4BPFk7uNsU5Ln1DJi8+Udi7YwOdfT+uXNChsfC81tsWr+16Z59YWQEZamGx0FgF3Wn2NZZFxU0il2F/7+/9vc54RoeWcz+FHy4C3ceh5vOQK5YUkmfdN2V9X7HVzAa8lb3FxU0Tr2s4c6LufsuD9eTHvlBPPfKROnfPXVWboxouL9fFmf0cq9X9RIB3O3hFQ89Ho/nictTC8sN59lPu44iAhcJxqXZ14lh18nfczr/tG9S/+Tf/plP167/+693mSIuM4/S1Hp/HuriwzBWJSywroZ2Gjz76aLe9+E/+5E+67cTvf//7Oyd9JFJc0XAgX40ddIbL4mUVVdyUQqtkTFvw9AVSHx16Xw3TkUs/NUCvjSdyslKjD448q3n4JCifS33Fh44OoL0fsIcMvK0PcEl09KEFuRL0eZgeNrEldGiir+dg37MR7Ss60Ptaeji/tzXd2a3+qxb0cV3avlRL15+tUyevqa9/5gt19nvP1Mne2dqu1bo026mV3lpNeivVm7p03q3zm5dqZzKu8WhcF9nUuby/32wUZ/aw1UlGndjnJNPG2Dh6fmdudAE55F/ial4BMXRgiC3ZyVlbi5OcXslNSzZlPqEnP7a3ZqEzpk4e2ORkm1sEocHXtpNnNuPRN6/EKvoyV+D45XgD7fx2lQLMrRyTmZ8WE348/fTT3dVL5r8LgT/8wz/svj36x//4H9e73/3usiFR4efVQm/Gs2MAE8H34Z5TYPQHP/jB+pu/+Zt6/PHHu+QJ8nve85767d/+7Vc55DKMc0e9IFkAfYyih8w3velNr6yoXBDkBEkgJELBR7fAWsQkxuTKQhEeMiQfXT6meYGxyZkb1WThJxdekgB6+snPRMikQ0sX+eSwn05btt2l184EMFnQ4SEPkGPcDkv+izEaJRN1PBk7kl7xbWVpubv03dnarjtvv30+QZcuf534AwnvjWtz++XafuzJesfLy/Xdz3ylTp27te7/jffXhzefqsnZkzU5v13XnzpbK4Plev7SxXry0vn6i//ySL3t/ofqHQ+/pSaj3apevlfqTH/VP36IE5vbDWv64i4O4imu4iBW8qb4zC+2hwEZaL785S93O3rlSS7EWzzFLbmUR302mX9uah51X4F88bdT2oFp9ywdDmh2m1N8oYvc5NDiYJGw09Y4P8FirjNH5NXPnKD3jY2PMGzFy25xISNteswN+m2E02dr5qZ25jzZeNlvcczNW7Lo+9f/+l93x6xY8IHOD3zgA/X3//7f7+UVp0IAACAASURBVGxRw2VROywfxo5tcWE4g6x8jz32WH30ox/tFgHBcaBwVrIfeOCBzjhJhxN4DnP0MBB8k0dgHJj3339/F0SyBdQ4OezgPJyS5NKVg3+/xUXQJELyTCBw8803v4Ij1+RsFxf+wGdxcZOMHvrForWN/Cwu8J7NsbjAZWItTjg2kGNcHMWID/wC/AXj6aQme4vXeG8yvfDs890EvOvOO2tne6cG+QYPg/1z3Yebjr1m/XGNa6s2vv18/aNrbq+7l87Ui5uX6qUT/fr87Hztnl6rpcFynb94qTa3d6u/fqKG115bn/3Yx+uOG2+vB+59Q7340gs16x+8uIiTg0Yc8jUn7frywSexkAO08OaGxUVcHWCHAR40Fhdb2BcXF7FKfh1M8iSuucdg4TgM5MZBl8WFDvZaXOjlA5tB5h+bzHM0PmIYT872yzV6NtHhYHdy87gLvcayOJo/WVzgzT/yPNlsjJ/8Mxaf2aVPP3vIpcPCSpZ55lkiOtCJu3GPLfDzn/2zf1Y+LmnTFT8Oi9mxLS6cELxPf/rT3QovaV/60pfqkUce6RYZVzMOpn/+z/95/eIv/mLnNEdcikmAZB0GHBIwq/Q3v/nNevjhh18JlokpKRwWGLSCDLJKOyhNUgsC2hz84cnE1veRDjg7oTOGh4+Liwtd+UEtB7+JABf5bNMnlxxJg3P1JR7sMZ7CfuOxnxy6bf+XbGd9Y5kone/TSY33zvYWF3l4/ulna8ezRXffXbvbO+VVmKDbcOcA2Ftg9Ke9ST1//pk6eWm73jg+VU888on6qw/9Rb3tF95XD/5Pv1VPX3qpTt94XZ2fjGqzerXjx8ee+3794f/5f9W7732wfuWXfqlWT63V9JDFhX98YJur1Pinz8fEWYz5Bi/X5gafxfUokJsvfvGL3XNn4qrv5CL24pQDLYuLBcGJyoEvtocB+9jgADSn/FQIHVlcjNMDtOnjhysExYmKT6ERjzbXoWcjm9jj2Tbys7iwl08gi4u54dgiV1zV6DKv2jYdioVFschbXMRIPv7Fv/gX9e/+3b/r8B5I9Unj137t1+ptb3tbfepTn6pf/dVf7eS3vnbGHPDv2O65ME5xADtoXv/619c73vGOeutb39ol5A/+4A+6g0uAJRNwPAvGlSwuAucAFXDJAvr0clgtYQpadZJjgrINfQ5k9ElqZJApccCqDcgCbXLTJiuJpMMiBiSd7EWbyGaXg8ZkyBkZLVkBfIBfCn2ZDLEn9nsT3ciO3IFHLkY19NzQrFe729t18823dL8G0BvOfcgmGPdxo21S0zpxerXqpfPVX7u+7pr061Of+WR9/4nv2upYt5y7t6q3W2un1mpreaXGNait0aR6u5O6fv3auve+N3S/meTRg4PAiURM2C6uDpI2T3w3lriRI1cmvgPgqCsLMRJDz8yYGw5I8aGXLu3kLIuMPr0O5PZqaj8fyM9CaHHJGV3O5Z8vdKgVgEd+6Xffgn/J3WKuw2d+sJlcfqgzR/DQAeIDWng2JK5iyFZ4bXHka3j10ecdLmTwSZwtKP/kn/yT+pVf+ZWOz/HpuBHP2N4ZcAX/jm1xoViAXL47wCwgAvO+972vM+Nnf/Zn6xOf+ES34nPURBB0CbAA6B8GcUzA6EEvWAlYxskIDg1a+kB0GNdOP3rJIJ9NoY8s/bYdfZGBL+3QRofaeGRqS7oSWjWZ8a0b2NMJF1o00f0KTc/9pssflXrT+dUbPt8O9awoiS+yXLW4kum6vXrmqWdqtrVRt9x3a9Vb7qu777u3nvzMl2v20U9V733vqrr1VG1Pd+pSDWpW7i+dqutOnqkT/eWqnUn3YGPrf2xLbYwPnU17frUxiU9qtOjkAU1wkbVfLTfyHB2xRZ28LdahoSvt/WTDxT72KKGHj1x0wbdy2IRGyTi+Vm+LJz9xskgEWj2xB458C0YrI7aExxgestEroVe7InOV8ju/8zv10EMPdQsNvJhaeCIntlxJfdnyK6E+hCbGtisd8gTJlQkanyMFAp7hzuCc4PRRgM6EUyI3PFkQ4NEleVZ4ZwO6FAsaXYqARaYk4lVaWZFHD3ySqo2XTDoU7UBkkIuuBWNioVbYQQ+boi/JDA36NkbowKLsyAlf91Ju+vfi62PQ/KPQ5eeFXMPcfsut9ez3nqyt/qjWVgZ18wP318tf+Xa9/Lkv19n3vbd7L8xgdVBbxcf5e252L23V5ssXavLyZg1WT9X0kBu67OQD+2I7f+BbH4zpq9GHp/W9jWXaoZcDvgeiSx9e/lIndzn7h2e/ejEfsSe2x5fwxi/4V3LR5As+vib/izoiSx0/Epv4oDa/+SVWuWKJn8HhT2njGtmurHzacIUCxIQsx4vjlR4Qf3IcdMgD/s2vsQ4YvBo0ZRyXMIZxGOhzBngvh0ssBjoYk9TciBLcgwr+BEcbXRyEb/mCbxMfntRo8KBRA234tkRG+DrCPf3GUtjQ0kZGcNHR6jWmv5/uyI2cyG/p8XUx6V6gsHfl0h90iwe8OOdjULfNn78pPW/9d1Uzr5d7S/XM08/VE88/VzWc1a2/9P665vTpeuRP/6zq8e91P67mt40GtdJdudDmpd7Xnj5dgzMnu70ybQ4W2yYp21ufu/tACwtv4oSO/cqirP36ZMPzO3rEJ/HSjuyM05EY7iezxXWEe/Hu4rqHaOVHVuSGPza1erVT0KMBcPhaGRkLTo0u9IvjGYv+0IUvckKn9rEznyTQ442fFhl9ABd9HeKQf8e2uMQRhjLGZzpg1WM0g7Jibu+9B9ZnSTg3l44CdFZPcjio6KctYAlaKwv9YjDavjY+cgKR2fa1W/n7tVu54U2dMXXkpw6NOnSLuJbPWHjV87jM7fe19GQ8vyLqzjZ+UqTbTceBy1I1FRPA65+efuKZOnfbPXXu1tfVxPt2r1mpt/7DX6rVleW68Gd/VjUd7W3OnXYPBOzubNXWzlY9t3HBDaa5oMviL+/mdcwo3ojnp010XUi5bzCb1Gg27fb/zkfmfqFhe+ZL50cre592Gx8xCbTxbHPWjrc0we9Xh449iX9sy/wMHn9ygya8kdv2tSOnlY1Wn+z4FL744rjTDj7yU4cu/LEvNTptx6RjN4sIvhy3Pl04punIcR75h9XHtrgkKJQxwhVL2moOWHAYmbvfHGq/Wu0YDvnHWR+7yEnQOCso5AP9BJpN6CxwxtWAbfDoXEEF0CjwSvrt+GI7iym/YlNokih9slLHZrzhMZ4YqqM/OH6jhwetjIF7Ls5mJqNvW9ynWBrWkgXexwC6s7DsPdg4X1TmTznju2b1bI0vTGuwIQZLNTsxqMHPPFTXn7u9PvLhR2r07Pe63zdaqkkNa1TXnVrv3iHz0tKoptcudT/KlgVibxV61QIzdpk9GHQ3JwfDpW5B2ZmOa+x1DuLTeXU5Trr8bX3eI9m3Eie08pAcImxzEMbkQizFfz+a0KbGg9Z9RHzmkivv5C+2tvOATcbRmuvRC68EtPGRqx1ZxvGY99ETPjajD61aPzzq1q/QRxeZkYXX/Ir+2EC3hc0YnEIO3iuBY1tcOE+xAz8LAAMSlIy3fW0OJSiHGZyFIfc28AoKwB+5rc4E1zja9MOHBy51xlub4IJPHZ2hkwTt1K0N2qDViRa0PkRP6tgUu9uzV8e88C8XJ6sr80UI/c6o++XoGvimKJcqe3zpdhH0c9KD1dre8WKplRra8m3yX3tNPfQrv1hbs0k98deP1mB3UuvTcZ2uYZ3oDWp3Y6OuOXuq+0G2LBCdZ1nI6ILwbKTJ793C2zvVbfpzVTt0desn2ebxQN7GSQyuFMLXxraVp538pY781IfpwiO/FhSxpc88tygAMiInNZ7MC/TRq62ELmORgSd+GGshMoLLAhBZLS+a0KsX5Ycn+tGkGNPOWPRdTX1si4uDXnEJZZXe78rFypegMVJgckAmKAfV6PFncQkfHH2LskPf0qEJXm2s5dPfr3RMe/pjnwmGV522fkpwePGQG52tDvTBh1cdmuD0tckFZIYPLvHOhIETKzyhj+2LtWN7MpvU7mxcF3vzq4mL3Qu3e7X2/p+p2XWn6pMf/Muqpy/W2vZOrU3GNbi0VbW5VWvTXo025vfXvJyh+2PbQmFtZ6eD04vV51bVrOzRefWN8MQrMVAv2rzYT8zC24lvcqafWKhDFx2L8hb7+MXY4rIY68gmq4XYlPFWf2zImHrRpnYseU9tTDs6wgvHRviUyA5NfI69kRH69I0HR8bVwrF9W5TLKqud4DvgAWezGnIuwXEQMN7K6DIrCTvIgdA6U6AnM0Egkxw0CaA+QIcejYInNrT2wePJim0s9mbMwRqIrvTVePGETz82ql19GVuMhzEQma0Nxtjb+pyzZ+Tgi0/a+BNT+lq7W3tfaXv502xSyydP1IvTrZpNZtUbTWqyvV39W87UXe94qD735x+u0aNfraX3v7MGuzs12/A4wCm/qFVrcmEhE4PuWqR5Q93elYuLED8x2xt4L0y/pt23OqOaeqq6V92rNSde/N2ccNiXWFzJ/BAPMVbbH5P4J+5iRH5iSj5adFciXywz/9DrK/jTVtOR+ahu598iHRvQk9fOWW32KvKNRh4dV5GBN/bwAxjjX+zL3FK38kOPjlw20oE/MSevjVWn4Cr+HdviEp0C4Qat78Z9RMpXzbl5y1jGKwJnx6qA2dF7GAiCezXk2vFosxQcEJRMIIGiQ7AEnn70bEIvwGjQJ2HaCTCb80Jim6v4g488NMbJgNMmww5dfXpNajh9iYp9xnxTxmdgy7aY0J144DsoubnpnYlGPjvYBehlDz1k2t0qrraSszuTqSNe+Neb9ev88xdro0b14rNP1ebZk3X60kYN/KzFoFc3PvyGuubPPlpP/vu/qHtsXlzv1/ef+l73rsunnni8djcv1TPPXeheHpWPZ/bTaZvyarbaA+UXCl7ce+T/4ual6g/cG1qu6e78PpgY8EMc5Ji//DnMfu6ET5zEto29PIqPmIm5eKSODrjDAC+7zD+xzc5yes0z9tGJLvMPDj2bjNEpX8bDl+MgPGqyow8v+eKneCQi8SGLTPbwzzid8q5NlvnmxM8/cYSXB8cE3eKrjYZN7IRPvCPjsNgcNHasi4uAKIwEDBQYxsLFeGOc0Ge8Ep6DDA3NYk125JPZllZ+aFIba8uiPeyIrlZm2i3vfnTG0dK3yKOPJ3ziBNfyJA6tnrQjLzx0gPRDFx3qw2B+8PdqOp6fmUe701rx7M10XM9NLtW5hx6oB9/6tvrmRz9Z59725uq97b7a2t2ojdqu7cl2TabzKwJZJ6uDvcVFGy5x942Rey8+Ns3GrrKmNZj6pntas4V5cqX208Fn9A4mdRsT/cRksY4O+MNgMebhi271Ig1c6Bb1pv9KXPbyDx8etX7ktu1FXHiyKMT/6EGvDR/axbHID298g38tcGyLC+OtpM4StiF7zkYfHnAo7RxMVlurptXdIwOHgUljobLqordnJkEgV1tJwKzQ8ORb6V01ZD+NBdAqjlY7ZxN2keFqB9BBBjo0aLNY5ozKL2Psa7ep68c+svTZ4QyCxxko+34yIehqfYlu9GR56lV80bOp5UNDPhsjQ3zpAKHtOov/Zr06//z52nn6u3X7udfVUs3qjDPh8i01HJ+v1d5KPfC7/6ie+vhn68Wvfbtu+KWfrxvXxzVaH9Qd991Vp64/W2s3XNe9OCqLS/ehdO/KpVM3mX/dKVa33nJr9TywuLPd2eUlVmz2qwKJZ3wWZz44sx4G4kGG+eG5mGxXF2+85CUHzuxwZIuXb4DMjcOAfOAqAQ+byAPJhxwlZ7lyQG+uoWeT+cMWdGhA+uSwic1s8myRne65UsErp7nKwEsGHa5g0NPFrughCz9cjgk0vqX1eAH54gHHJoUfrS/sy9V8Z/AV/ju2xYUTgpOgcQ60BhtXAtqczmVc8PvVAhNa9DngBYHz6kX5aIxJmGQlmbENPVzLF57YYDx8DowAHsA/PIp2AA+bAov0fEmsWrrQp8ZnXHz5EntjEzq60+cb2ejFiQ4T51CYzRe/Cy++VKvjWQ2Gs9oYbdeptfXqD1artsdVD9xdSzdfV1//whfrzPmLNTszqGdHF6q3vlTTmd2cJ+cb8tzLtc2O75fD4aZOjcbzq9opP7p7Z74tcsNnWrU07O698DUlsY3fh/mAR575jD65iu9tPhKrq5GPx6JCPj0g80g7uWxthMv8Qxv66A9t8JGDRwFoFTkGFgq+RgYdcs3P0GSuoREH/SwekR35ZBoLT6ek+Zf516CuuHn5SL9ilv0JOd0GIY5m4htjaPCCkhKHjcEdBPgThPCgPQifSapGH92p8UZfbEk/Y8Hrt3z65JoYkd2OL/KhjWyxMFHxxTbyQGj2ul0fjuzUxqJTu42rhUXfpKJnUV7kLtajyaiuO3266uKlOlG9Wj11qnynM3GbdnW5/Fraz//v/2s9+/1n67t/+ie1W6NaOrVST33/qeov+RmAcfdzIz7yjHd2X1lYLCQd9Hs13tvPMbD/xoY6Y91rMudvymNra6/YgBY3F/aD//kcujYeWQhwJD9qRQxTflDiqzGRnXlsNLxkwYPIDXd8aPFk4Q0YS4me8KUObcuH1jjd+PkNzK3I0TcWvPmqT445kjHjeFq+4FqdnaAr/Hdsiwt9DE1ZNDL2JACCoq0kYdqLwQyfOrShT0JbnoyhT+DDp46crrHPvorwh4eMyA8/3lY3fErk6i/yLdoTGa3c8LRyIlsdntgZuhavnfHgQ7dv7Rj2LU5/UGvTfg2mve5bHBf9fsWouy27Pqx64Fyde/CBevTjn6iLzz9XJ/u9Wu3erTvufplR0w+oLefFVHvbBDqdeycX3xZ10O8J4rztKm8vXolF7G99nhMf/L/laeWEIzh15OK5khjJS8tDZngjFy40GddvC3zmgTZox1sfMtbWra2ZKy1/aBfHgk+NZ1EXnvChA6Hb615VdWyLi8XEwrK4+i0au2hdHFrkW6TTb2nw6S/CIi792BY54YNvIfSLdIv9lq/laWXt1w6tOu396IJbpAtP6pZOO/QZTx26g+pJb1o29i+P3V2dX3iIzGAyv3qYDEZVd95QD/7yz9dz33+uLj72ZN203avVixvzhcW7dTH4acbs75eexNfZ2jADiOzEutPbGf0DZrV2t+0fIGwQ+9G1uLaNbbHfiDqwiSd8bbtlaMeDX6Q9aP6EN3ypg08dvHo/XDt+UPtK+NBcCd1+Oo5tccki0dYU6gcE1CVWDNZPgU/JuDrj4W372mhy2Rb6/fqt7Ha8bUd2aNMnF4QWPu3Qpm5pF+2LvNC2MsiPXHWgpdXOWGhDt4jPeIvX3q94H4xdKqMy7tcBulWi3DXrfoe6qjbgl2e18s6H6sZbb6pn/+un6twLO3VuvFTdg9JZXLZ2vRpvvjp5LGHvapGO8WxSk6lfcpxvsoOzuMxm0+6RhTaXsT/+72d3i2tzH57ENDGCB4ljy39UO7aFLvrSb3XAAXVsSR39+mS0/dCkzth+dexJvcgTG+DbdmSFPnVra+xqabWvFo5tcaG4vTzLopK6NSwLUC4r1cGFvu23ODp8bswlXcbIDw+axX7G9qMPLT7j8SPt8LT1YrvlIa/tawcXmRkPXm0spWNocKFv9UZueFPDR07oI2+/ultKlqomw1lNh/NfCFid9mu5bHjz0aVXKysnuvsqrl7e+s631+4nvlJ3P7FR92z2avr0S1Vb48tXLts788Vl5jUve98Z+BjELh+LXHV2/fmJJ222xqe04/d+dre4+Bv6+J0abdpqdJl/7Q3VVmbbxnNYCS25i3qCa/GRFbtid1sb0w9N19j71/JDhW+/dvRGVmjbOvJSt7pea/vYvi1iQGuYlZDxbjBKXsbUgSR3cXFpaRbbLU+C1dIE1+qAQxO6lia40BvLeOqMhbaVlba6pQ8t3rbN/sQm9KlDlzq8+mgU/CA8XafpJ5ZtnPajD5/a+Xw26Nd4aVCjYa+WPNw4sbDMauamcPfkdPf5pWptWHc/8IZ6cXqy1r+7UaMvfKue+3//pE7/6m/U2j33VK2sVnlhuBu2XtGw93R8rzd/3YN7O7ku676CFh8nlz2D4lf8bevW5v3afF6kjzz0iWtwbYyC209ucC093H48dERPa0+L12552zH4lFZHZO7HF/qMpQ7/Im9Ln7H4uFiHdhF/Jf1jXVxcTjlwLCj51sLXZECgXYKBnClCl9oYZ9pg5xKNXPjQqsmEc3c8XzlGhzG8LX141PRkHG0gOH2yEnx4fXfY1WTwI/LRa6MDsRd/FhNjuZMfvshlDzp9PLGPrugLD3vRAnQADTz5cKFVp98R7vNvNKjasc28e0fuqNZm0+qNxlVL/RrNxtXru36Z1mxn1D1H9ORj36j71s/WxtefqAsr361PPfNs3bjbqzf/o9+u5Xvu7H7+dbIzqv6yr0F73S0YP6LmgcWRLfg+x/vb+5aF7UPvl9n7Vi/+tT7w6zBoc4GPzPidb0XIINt46ug4Sv4iffKW+ZE8tHlZzBtd6OHxkwn00449ajTq1o/4QI+SsfClr6YLnuy0Mx56ugFdCkCj6NOH9rXAsS8uDPH1H+MYtr33EGMbVBPBuA1BNqyht6ksjqnRgzgskPjwKB4bCB2dJhBAhwetNjr0+tr0Zl8AOm12oo28bKKzWS/6jUUPWjyZPKG3uWkxkfxAH3/o047v/CaXXejoM64fnfSIET1sMgaHLnLx8hEdG9AmTnB0HATdPdtLWzW5tFEbmxu1UoPu/bj91WG9PN6stdVBrU+mNX3hpXrms1+o//Knf1K/tX1NrU4265rRcm2e364vf/Av6tQtt9Trbr2mLo43a3s8qbXllTrh9Q2+dV4Z1nhju0a9QW1tbnbPFo2mkxqeWKvt3e1anva6BSZ+8C8+qOEPA3FInDI3xEEM4BWxV8zJbP8n24kp8+8gHYlzbJIHcyA5yLj8KXSzGb34h948NW4sOU7O6WZbbFIrbCWDnfyRSyV60NDPb/6hyX4YNpoX7CED3rjCZzLEBmgr7FK0o+uguByGP9bFJZPejkHPRAgGZxNQTjCYo2gZLjCczhv0DzJWkGyEU0uAnZhqILCRq08PHB1oFLgsQPpsk2DyLApq/QSfHM+osI0cRZsMbfRJoKTSlwSTo8RPusXBDk21ZOPHF9vIxMOP2M4GMcKvNhm0Q4cHkJUJRB670NIlD2Ic2o5h4V/PYry1U8Pz23XpxfO1cXGzNnZHtby+Upu7W7U+6Ne14vfc87X12LdrePF8vTjbrTtuGtbw0vfr1t6gJifP1hOPfrzOvP+N9Vht1nD5RK2+NKsbLvZrrZZqvL5Ss81R1cq0Lr14oS698EJtTkfVu269tsY7NdyY1KmV+W8y8R94tzLf1Pw4DPht97I42ZWtyDF8YiN/wcmFOIpT5ulh8tlhVysZDkzzDy8wJ4xnfpGbHIo9m/KzKpk/8hw6tOnLr3nBZjyOJXrJyNw0X+UWn53n7DHX2EQmn9EAduEjlw5y+aDkJ0zQHzX/OmFX+e9YFxfOMl4w1Dk7aAOOc5AjaDmVoOYXAQ6yH68JkYCiF7gAOQIMkjRtiaJPgE0+QK8JhUeSJCJ2SL6zDLCdn44cmPgyOfCRiU+iJE+i+RxZ7GFvEpszEJzHIyyWZCQuqY1HJ14Tiw7+05Ex8ukyzi4FHTwce/ksH2QfBEPvKZldqMn6el17+mzNTqzU0nRWyyfWam13q071q67Z3q3h9riWr72hzpw9W889+0INdnbq7vVr6sRoWv0Ll+q+u+6uE+tLdWr9TPUGy3V6tFxnBtMa7Myq/OzK+gt1Ym2tzmjbUev1Dteu18Zos06cGtT60vwg4D97+SDOXsEYnw/yQZzEh6959ERsxSDzT2yyuGRuqtHhOQoyN9hjbuQAFm920pN8k5WYm0Pma3KERt4UkHzzAa3Fgj108FvO+cFOpV1ctDMv8JDFz8xp8vicOWgciC0/zA+y+XDY/LNYXy0c2+KSQAlgkqwWdIYroUlwreoA/qhnOwSJjARZYPCRJXAgk6jFG8crUYp+JgIebcEXWEUyTTggWcHRjZZ/QAIl2nh7IJsIdIQPLfv00Zs47MuEUKOnFz62w7W8ztx8NkkziXPAZeLwg69kONur8YDQdp2Ff/3ZtJ7f2qnVE6t18tSpGp48Uau199qG6Vr5sZSVk75e7tfKvdt125veVOc3P13f3dyoG69ZrxdfvFDrZ87Uufe8t+r0tXX7+rA2p5O6vn+629zb/aj96nINV1eqv7JUqydP1AnPY/UnNVpdqZXV5Tp1crVW+pfvy4lpTgxidNTBz28xEwP5kwcHWBZb+UNjHE4ezSVxJf+o+cceQAa54kqPGCd3dAC5hsfDJvrym0L0whlXkmc88sgmVytsosM4XzJP1eZR8kye8XZu0Js5jQ5NbIpO/RwTZJpTrU2xK3PXj/hdLRzb4sJYQVY4JgHaahCnYjQcpyUkfIcZnwOZswqeLCaCuZ+MyA595CfB+mxlU2SFRr2IC23LR298oo/sRYDnP1rjmajRG340geDamhw2RF5o2Rk68jORkpNF+vCltoxN+rOadvbxYfmVx4J6/fke3ZqNq06frbrndXXfz/9CfWt3VE9+cqe+f+aaevKl83XPDTdUnbvLabhO1bB2xpvVW+55xV3VYNnLXLpXMuzaL+Nr6JXlGvZt3KvuK2/vegFsBfxJTvmnfRiYZw4SucYrTsC8AWKb3CSP+vRFV0d4wD9y5E1MFTyRF/lhbWWmnbzhA+ocE/r84yf7QeYLvcbwp8ar386X2IQmdrX02pHbNfbmvjb62JOx1s7grrY+tsUlxnEygYkx+jmgBDuOwqXgOwzwkYNOAlp6uiNzUUbonRHoIkctOcacVZL48BrfD0zeJMIZIbLINpazCXta+xbjEZv4w26xvgAAIABJREFUYWwxdq0/bEFHtjZeeiM/MYld7A4OjTYI/X5+9Wyes8HWI0Lzud99Naw5nczmv87YPQY0qDp1uk695z115+5OPfb8c3XhxhtqPJrWS6Pdut2V6O5aLa3NanXqdwUcNc7QfteoX6P+rHqzaSfP+mL3bn/QL7+z1G2n2bNTLhMTIlp/97O/pVnMXeIrhsYsQmrxCi5xPUh25JOFR1kE+YndoRdzso3laikLZXLEzxR88HiiI/OaLG2yLDjhV5t7mYOJFT14jPE5/OSiVegBcOEjb7/51xFe5b/DTwdXIawNAkcUoGa8cQ6EzlhwCbj+QaWlb2UEr14EdAIFEjA4doC0F+UJsLII6BSyyFgs/Gj1tToiK/zki030tPaFZlEP+bHdWHiCi46D9Mb+/Wob3KZ9y8wc+tNZd7wPprPq+/VGO29hbIq75dY6/dBDdf7G62vr7jvrzve/r56+dKFGn/pM1cZu1ahXZ1dOdvx237oqwj3p9+ab6KiwM9cB4wza9266y4tiN7y3QIvRfvYu4vCIJbx4qEF7kCZOGQvtlc6/xFu9CNGZvBiHS84yHt2Rpd/K087cICNjsT164eEWC3nRgTbtyIk+dWQaU+BSgov86L2a+tgWF0oZlMDkoIkxjGR48KkzfiU1/iSLrkwc7QBc8HAJUoIGpx0gr5UFz7bWPvL0F/liDxkpkZs6cmJT7IF34CiBjKkD2pkEcPqRqc0G45Gjjq3G0GQsMhdry6ifdLU1v9ueb4v+ZNotDvaf2LTbvRLB53L2Lg9r4/TJerymdfHmG+v1v/4rtTHo1fc++cmqi1tV2/Pnk3quDMm1H8hNRPtnLGJ7BtjvQvRy7/ImuviGJLlM7BbtbvvhSzyMweXsnFzBJ4bh0T8KQtvO48wLvMFHFvq0M97mEa4dj49w0RWbFmW14+jNPVffCuArMLafTuNtnDriPXo8SmA/GRk7qj62j0UJQAxLAPQ5op8CZ8K7ZEs56gCIHA6FXx09wbf9tu1yUgIlgq4EHS72JVgtH5y+YqK2fGThh1foCPALDxry419kR2b6+NDox1dt8hWX1YkVmfSh00482EZGdCU+kRnbfrCedhvbwqvuzXo+0czvvczcu1jurjZG7jX0qp6dzup7k3G95LexH3pTrd12c331sW/UrU8/W8unT1YtL9VkultbdvzWSrcL2OJCdjf1/aTIbFqDzt8ftIjNaOO/9mEQX0ODPjKCEzMfh8QxdWJ6tfIjm97ohqNDnRyZEynw+fiqrbT87IRra3ZlfqKN7S1v5jbd+bhPhtjhNy/w+TilH3vUQJ25E7nRmfh3hFf5b77EXSXTfuQcY7igxlB0cICRDGe0go6zWXET5INqPG1g0OXA0k5S4JToboOFDqRu2+EJrqUxRj+/AtFJfgr74q9JxDd8xsOrDfRbW1u5bZseRaxaOxI7Y3TSA9CQLd5yAg8XOQfVfv1wuLRUK0vLtTxcqqX8ZIYFZjrfzS+Tw5OrNVlZqQ03Qs9eWy+vDLubs+/9H3+znn75hXr8kf/afSzyMOOwv2dL9xuNVWtLe+/KdRA5w1oMx3uPYO+9CrONEx/dL+DDQXYHHz/FIAcNWTmbiztaIDcZSztyDqoTX3EF+niDF2tAH7sjX58P+kpsSJ25I0cAPn53iD1d9BjLHEg//OZAjjF8xpN3fTIBeni2aAP2BWKXvnZKxq+mPrYrF0oZmwMshicI6hZCKyB4WqdaurTRkyEQigBFB5rIb3EJjEBmEqFtdbXt2JFgkxW94dOPXDU7TCD4drJFrjpy4gscWiXjamUR+IU/EzP0odMPDVzsY5PYhn4/2ZHhfS0+7njr/3yCeg+/fPWqb4Z0B/7ec4ndR6iq0bBfO3YCT/k3rZNvfbDuefiN9ZlPfrLu+Zn31NLPvr37pmhlMKxLs3GtVL9Wh0t1oobdDVwPUXuI0d/ln0S7nBv2LpbL9v5gi9/iwO/ENfFITDJHglfTkdj+oNTLmMiI/FaGNp0BtEAsM7/pbvUbb3MSHjTsCS2ajGkH3+IsHArbWpl0LNLnWECrDcx7dIu84Y+ujvgq/h3b4pLgMtAq7jLegecsog4wFI2gb+/dsdZ22XYYkCmAcVQfH1mCEx3a8AKHlv7Q5oymZq/xXC5qszkBZ4s9KWTRS0/u+Gvjk6DoU9PT6pAwhezYaO+GfmyiA7AHjTHyMylCR67CBmNo2Rr5xthpHD8+NPB8iLwDYzzp1XQ0qdHObo0GXiNaNXSlsXefxFfMu5DeKOenQLyWoWdR6tX2ZFJr152se9/xcH3pM5+vJz/52W6hqVqp6WBWm6OtmtW4lsdVK/357xyNl3s1mY5qbeCgdDBaweabu+SSzWKckvweZD8/Exe85pb42EslLviTM2NyJ1b4xMrYYYCOPDElHw9+kDyEHw0InT6dbIgfmRPo5AsN+2NT7DI/2E+WOcJO9MaBMbKiS9sYPWSyE5DLzsyN+KymwwkV/UHzrxNylf8uH/VXybgfOcM47wASTEYnycYYz7k4GVoTwFb7w0DAbCyye9YGsRdffPGVACcg+BOgJNEW7WzTphuwKwuD4EqQMXZLIPkADb12fdLBF+OA7bnCse0aHd2SmETHV/T42cQWeBulFLjYENuNZ9EgS8FHd3yFQ6cAvMbpJ9PmMO3Ydtji4qXau5u7tXNpuzZfvlg7W1u1uzv/GY6Nre0aLC13H5m2drSH3qNQ2+cv1NgzP1u+1tyq/oUXa+3WG+qWO26rr3/xS3Xz579cJx68t17YHtXGzD2jfm2/fKEGg+V62S7owaSmvWmdGC7VdGLj3/yjG//4wR85FmebxOTmMECHj9/iqg1y4OTAlWt5lDs5s/PUmDl5GKAl0/wjX1zNW/FPDpMLcuD02Y3OVn78wfNPAei02cAPsuWX3+aieWiOsJntWRjxmpto2Mc3MtDQI5b4ctzg46sYKaERAzRsyPxCp5351xl6lf+ObXGJIZxUGJqEcpiRMVyQBTS0apPgMCBPMAROceDgA+QaJ1NbSSAFVyE/OtTswWNMncRqkw/oME4venh9eozRA8hjS5JLhj46ctWADHz6JpE2XGzBR6ZxsQP0GVenoInvaPUzGeCjZzFOncB9/llc/G7QZHdc491x923Ozs52dyWxtb1Zg/FuDcbzHa3uywyXhjXZ3KzZxmb1trZrPBrVi+OtWj27Xm96+KH66J/9VX3hI39d7379XbWzu1mTpX4t7w5rtj3qflN6sr1b46VJbc9GNR2Oq8ajmk0vX4UlDnyJz/F3H/M7FJ/FIT6TkTiLjb6Yq8UdLrLVmRuHyccb+WSQRwfd7NMGarR0wCuZO+ZSxtGEXp05mLlBh8IvOshLHw3IMYGGD2TQBR8++tigbzxyo8cYXvagQU8XEBu6Xwsc2+LCIIbbEm0rsgNNmyMxNAamzyHOKNddd12G963JFzABsKJ7JkIbHn+Crw2SRDYZszLbOo9eUC1waAU2CxG56DPRbrjhho7XOBn4tEHabCBDYRPfYw9dfNXXptPZR9+Zw5Z2MQrAhxY9IF+Cnf08i8QH0CYcDT1sYwcQd330xsk9CHwrdHH6co3Wd+vM6bO1tLpUu5PdWjqxWus+XgzFuFej8VotD/nfqwu25C8t1+nhSp1cO1H9M7fWYHWtzrzlLfXVj32+nvr2EzXe2qmb77qxXh7v1nWnTlb/pUvdE9fXXXt9ra3NamO6072j1+scetP5IszO5EYexFlcM2cO8iFxE9PEVS4daOKQPJmXZObKxRVhts4fJBs+8uWFfFvnydFXMq4Gybs8scH8NifZZKzNSXINL2/mBp/lTizYjF7bPGC7OQH4xn7zyPxAYw7kWEEXerqBcfLIZ5dxY2yPH7EJHRl/qz8tkqBy1oHsci0LTJzqPGv+CYBgclayjgI6BJdc8vEfBhJLvoCbEBIGEkBtgVuU8/TTT3d0OZC7zgIt2fxSOwjooUOCQeKRiSdJ6NnOX/YrJkZ74LS2kYOPDk+wmgQWwEV70eBLnNGboOQuyo8vr6r9tMiF7Ro7MZw8VYP11VrvTbqXPZ1YX+0Onrktkxq4wzuretHisrJSp51E1tdrd9Cv4S03Vd27Um9/1zvqI5/+dD3z5a/U7Q/+Wg1m01qdrtZKb1hLNazla07X0gnb/ke11L3tzn6XYbcrOP7zSXwSM34cBvjkMnNPLsReP/FKrpM7ORNT8+Oo+Rf5FhR2ycNRQJ+54Zggnx2LuSYjB7K2hYiv5LOdbUpAPBZPSJkXfM5CGj3mWsvPdx/V4OkgC39sSPyjL/Mv/aup59c+V8NxAC1jGSKgDAzAKXAt3njG8FwJ4KdHEaTIS93KgENjMij69C1Cgho8upYneHVLm3bkxpfQG1+kQZsSP9IP32IdGQ4EduHD04KJFJya35HfxqnlWWzvTse1YxOdrfrdRdPlKyfq/FKin33t7r3KHT2KhbT6tVuDGveWqm6+tm5791trbWuzvv2Rj1RtXKjl7nPXpC54J83eJXbPDePuJZrT6rl/tLe1Lv6Kp3mRXCzau18fD/p2DrbxzQEXXjG6Wvl4FudrqyOy1ewR/4Ny0M6R8KElXx0Z6ja/oQ2eD4fpCD0ZiWvrQ2IeurY+bKyl2699bIuLFTPJU+csqq1wSlmEJEZw9htv6clx5qeL06HXTjJCDxfd6jZILW2SFj79nC32GwtdanKjq9XR8sYO9sI7g2mjF6f4EZn71Wxqz3wtT2Ti45sSm+Ba2v1kdzSDWe3UqHZdsZgV3Wdu3wZ5Q5xLeT9aNph/Q1S9mnjK2I3dmtWuL5HqVG2MhlXrg6p3P1j3nj1T0y99uba/9Pnq99wf2K1tG+rOXjd/jmjXq128SnNaO9tecTFfMBM3cWnLQXYHz9/4jE/MgToyUycexsTUfDoKkqs2B+RFZjunFmWhSU4yFr70U8ePtq8dm1tbyeCDuZF2S6vN3oBFCG10OJYWwVgL5B5ka0u3X/vYFhcG5EwgkAlGlMbIFi8wSg4wY0qc2Y8nNKlDkzr61JHdykeHN5B25IUPL2jx2viDTx0Z+hlP3RE3Vz3R3/IkodHVjgWXWKlDH1ntWYi+TJ5Wd+TsW3v7/qDfle7BRfNrb45NJnzW8fY7cXOi8LjA/LeNpgOvsZxv31/ysic7eYfjeuC976rZ1mZ940Mfrtrc6R4ZGK3069J4dy6bKBesbib3ZjWdza9E43vixxc+72v33nwxllikju9t3cpGl5i28+MgPYlrK197ER8c/H7y4VsZ+q1drf7QqpNz7UBoW50ZS73fWPjUxlOCD696P1w7flj72BYXzueMkaBSrJ26xQdnZc3ZwHh7YKQdGXjgErCMq8PbKdv7B8emrNahWZQXnna8bS+O60eGWqFHYUs73vIuxqeVEZ7IC1/rm7GcibTbsdDDxxa0++mMjsWavNgfeS0uY9Gt3+nrzx8V6Fu4MU52q37pvbV+6831+F99surx5x1RNV0d1ng6mr8R3LTYW8T6ftFxT3d0RG/qRVsX++ZE7DEWCJ1+8MlT4nQlMcLf0kVe7I2e9DOe+R3b4Nt26IJv+dux1nZ4EJ3q+BL8nOLVi1Jk7Hf80JsS3sgKX4u/kvblLFwJ9RE0jEhw4oCVDywabtwVTop+SqtmEZeVNHVo9wtAZKtbOdr/f3t3/mTZcd2J/byl9m40urEvBECCAAmSIiGQIkFKpDiUOKK12GMrJvyrf/E/47/A4QiPw+MIO2Ls0VihkWZGo9GI+06AJAgS4AaRWAmigd6qq+ptjs999QWSV1XV3ZiakUj3qcjKzJNn+Z6TefPd996974bSho9Nsu3nFXhtTJFva+2U2KUXmfAiE+yHjbf86OR9OHwHEZso8mmnDv+wup+r2OuM9v4Zi3yHy495u1ZmMutuTqyNtao7TtfbPvSBGrx0obb/8ovdg9MWw3nN/C6ML7TA9XMO5TEjK7V/x9HrOYt9NR+H4Q6fDFzpBz/9UDuPePFxNfbJ923rh651/bW6bRvuFLYTR/wkHjraxrVT+jqtfnRjP7p0oq9uKfyWd7XtY91cHJRtwEAE7EGbSxtkCzg6ba2dZLSLJLxWv7WbdqvTyoafmh+LLQuObMZavX6b3mElGDMeXX10WG0svskkluintrCNodjKmP7VlNg2f5Fnoz1ogiV+6JBXVn3W66c153tVm+tVG4M689sfqXfcel99588/U9Pnflbj2bzW/HiUm5WE7uH03bMCfEW6/z5sHzgMrf1gOqqGL3jJBee+yder2Dgo5oz169hq7UbGWJub2G3rdvx1IPuN2CEfIh8+XvzKNSIbXsbT7+v1+Wy39lu/nfFj+nesm4uJVQDPJKsTbJKtT8apnNPGfECboJOsxIiP1GTbkrH4SCLx2faWKG+LIttiwqMDW3R80KXQx8tEJqbgT42fU+Y+5vSDC5bgZz++Yytx6keHfXjo8hOd4Epc+MHCtqJv/Eol9pMrerGnVlB45FJWV1e6b4/WN9ZqtH8WMvOBygNvqwc/+JG6+Nwr9fPHv1eblyd1gxsfVxxELvf3NdRybuMjfmF/w/7yA/yjYkhO1fRih05spzaGkiPyR9mODTpk+Yh8cpK54AMZ79uPbMaDh2x4sR8fiSOysRH7arLt+kt8dGJbm0zk6cRH53wfs/H4in7sRe5q6zc+Sr5ajSPkkgiv+jv7Fy/5nl/C8ooIfA6QXCTlU2yXVRtjQ60gAaam5zqXfC2b4DOxdLURWUTWGRX7uW6CPwcT/bTJ5GDUji574iGfWNjOJ+9qF2KxRSZ+6SQOY8GqhlMcrjcwwbFljD/jir68saWQo8cuOTU5BLPrFdT02DYH5BHeUcQ+XfnKfMmHmF0LEQxi5DvzQGcy3avLfrzbZyezaV12uf+86uTuTq382rvr1H/4bP34b75cN/3OB2tw5kydv3y2TtSmW5Pq0nyvFqsrNd1d1MpguXHGf+aOD/EcRcmDmGFG8OsHs/yJhV08fW31lezLtbkgxz5M+lnXmbfk2TrAY5us9Uc2sZEjw67cIjHAC1Ni5w9WuuKRd/Oc+WcPz3hks07Z5ptdbVi0Yz96dPGDXTt9+sHXgbyGf8e6uQAhOYJMUJIqKZIBvCAlNUEaV3JvET6ZlqInkbknx30nbCLJSYLCc9Cy5b6LXFBGlm/YsuC0c4DDafHZLBBfJkpcJlRsMLDb6sEOM5wmEBlHWWRw0QsPfhf1sW2y2W1zFFnjYhNH8kgOn8/IkYGRf3xXVMLr4q3Y7Zwf8k+c7jERMxswZTG3mwsf7JOT1y6/Fy7U82dfqjM3nqm16bQuXjxXq2dO1M7Lr9Ttpzfr1Nvvrce+/HjdcPsttX33TbUzWa+9wUb39fYrNanx5nrNL0+65xbJIR9qPuC4mgvWYJULOnJrfvXpJy/mRCziS0xi4EuOrkTkyLv3hw+2zQPK+iODzKc8kZdXfT7VZPmDObpqawW2rG1x07U+yRvP5sKP+IyRV3vxFLe5jG32tGERv0KeXRfdwZO1FOxk2dY3lhg7sNfw71jfFgGFJC8JDNBMvnGgJStjApQ4JTbaGPDaZLKl3/qITGyzbxwZi31J01cQeUU/OvC0i6Av39okZ0ITQyYldtXoIP/shh8f/Tp425y2uNOOXzHwqc+2Nt2+3X6fLF7k1Uorx2YK+eTJvUYbp7bq8u6lmlzcrRPDjfLRy2zrZE1Wp3X/H3yiNi/u1fypv63hpYs1HM1qMprXYmVQ04u7tTlY9Ri2Lk/+iUFBrf+j2g4AeOHKgaXf2mlt48sLGTEdZdsY+eRU3c4HGyj+yKbEbivTtg/Ta+2zJS4l8rGhD082U/z4ZCO4Wz0ybYkNei3ps628GTrWMxeTKkiXL7t0WdtOaREKRqAJHticvtG7/fbbj8RPjx2yXp3cE5GkU2wTSjYT4ZUD2dU9PkKi7OZ5NUg7+IznzCWv+njs5dVc22KODfZNpNsF+GFL3DCR1UfswIzct+RxEzl7yRjZTCo5dvnyigWPuMniqxU6+nIjHjwEr7zSTz66gQP+eTWDhQ+vaHTYc/bjlT84zCl/zozImeuTJ7dqeMNqDSazOnnZL9WNam9zpfuNmNUbt6tuvVDvfc+v1VPffrJOn/9w3X37O2tne1Inb7i51jduqPWtEzU/dWP38Yv88Msf3+KBC4ajiJ68JQZnCfpswKydtSgveGzLa+6xOcp+5gUOdqwlNb+ZAz7IKZn3rH3zkFsRxBYZOnKN6MDmuHAbCR/Wk3XGB1n5znzgyZUzZ/w8vgQutmDTzpyx7WzIOwt6N998c2eLXOQTZ9ZQ5t3tJ9dKx7q5ZIIBFZCiLRCgkQQhspKaCbnS4omuyYpNPP2MdY3mH5/GJYp9hb9WH7bYgCkxMJNJTaIzmWzELh/iFAt5BWW8gdM1TRaKLLn4x8/kdkL7eaLDNzl6MPeJTBtXFpT6MCytjcRNlg4/4oxfsvEBo/HYHQ4GtT5cq5W1qlWPEahRrY2qJitVe7es1trGRt398Y/W1774N3X26R/U3f/4w7V2crVGa6u1cnr/Hh0vysM3fMgn+2oYrrQ+4E9u5SHydPXV4kJtnpLPyLc5adtZp+Sjww7+YQSPuSJjs+ODjvwpMKHkMXZaH7m/KOuCvoLwEB/RYTM+jeFHXl/beHSSk8QRP53hZv2lfy31mzvfuQYPJh1l8tUCULTtrF5BwjuqJm/3VSy6vq0+LLbI8WGiFbwswtZXbKnhUVoe2/TwEk/qxKDu2+yE9//RJZMYtBEdZDwl/PTJiiWyncL+v8hEB07ySmJucR3UFi95tmJHHf2O2fvX2lnuDb5i9mBowSwvZblox1gfVj36nrr1vjvq+1/8cs3+9oXuN2J8dd19Je1jKl8c7a+JxMN3SuvrsDb8yW3iADntto4v9pPXw+zix4488YEin7GO2fzjD6aspdZ/8hocUYOFvIJaHf1g0WbDODzk+Wp12nawqskpLYbIshefwZZ+Z/wa/v3dl8BrUO6LZte0E9sZUbtrGs9ujU8usuH3bR7Wzw4cPZOSdnT0ySl2Zv3UZNJWSyQ5MjAhtbEk15iCUnedZtLJZzztyOj3i7HIsQlH+urwEkffL334wk+NH1uxExwH1ZmLxB47dFs8dGOPTPcK6NW4Zt3TApa/i8n50outauG2pLtvqLf/9gfqiT/9l/XaZ75SN931lloMFjVwe7SUDZZ2Y5tdWBwAXn2D5yDseMazBrQjn3VIJnkyxk/mu5U/zD4+HTkNxYd+bGdMHbttHb6avbbf8jKWOr5SRw+elM5Yb21Gnp0cB+1aynhrLz7VxtuY4+Nq6mM7cwHA5GY3jfMABbINxHjAC/ZqKEmMreiF30+CfnxEJn7jL5iiS74t5PpjrQ2LSszRiV39UF8/+OM7cupWL308sv0x44krY7EJk2I8vNZPv03mIB+trlhRYlYri7mNZf/COCvKdXL7+4ss7No5Ti7qpvfdX3dt3VDPfv7rNXn+ZzUcry0F3/hFgdexJmb+M899zP1+e9Ak52TYSp7ST20suevb6/cTb59/VD/2U5Nt2+nHhrGD5iHjMLQU+T4v/X4e8NlPiVxq9lrqY23HrtQ+ts1F0NlY2onEQ0C2gWrnAOgWaLMDR7+tYz8+2Iw9Y7GvraC02zo2O4HGRvrq9rS05bMTn6nxYOrbbX0mB2QyWeo+GW99GA+vtRd+fLJlPHzt5Db5iuxhdavTGdr/F5wH6dHpXlAmszceDyAsV+t2Dz3zmy37P7+9Oajzp1brg4/8Rp3//k/q2c99aSm0t/ww83Xs1oFTfrb3T/vb/B6EAy8Er37ykTp68aNOzGLI+GE1+TaX8Rc7DtZQbLQvtnzhRz7t9I23MrHFZ2TUbZ88yhx1nd6aTu6MRV6b//SDJbz0+3Kxf7X1Gxm5Wo1D5CTX6avTUK8gbcDAKn1eTGXM+GGF7EFjscFnduNMdCufMbyMx6a65Ul6Et+OtXFFXh1+eNHRD4bEGB4dhB8KNnWIfHRafuwai3864afu64ffr1sc7KRPP21zS4+/YFr6Hy8fHuKqONAH8tk9wbW8OfYL/4sa1893p3XL+z9YsxrX9778japz52tx6dUqP/NgSzH/Hkbvhmkf7ipuD/Di0f+TIxe27RdZhC24kr/UGUuO2jrtfk7afmTYV1qKXHjpqyOfnJEJL/L6kY1ufPRr4yjyxmM7spGJXPpqc6lOOzKp2Yg8nn7s6l8L/WKWrkWzJ9t+QNR+uEQsrwz9AzZBJlCBH1YSpHF21CHJbfvht0lqx1t+MKWObltn7CA9PP7JRK7VNQ57xtQ7OzvdB2o+iMuHcNGJXNtveS2GyCQn+mTbWCNzpZqOOPqxmDs2vQLmVZOt9OEZ+JHx4bh7HGy3SZgbPwb1+hR5HvR67eyOqx58sO58+JF69ns/qp3Hv1mDwU7V4nLN+bFWBsv7Gvfmi5qOR93zpfemPqj0CXFTli6WT3KEx6c++x/OqpOD1IkB9vBSh6d/VOli7Z0lxkbqNs/mPTo25lYGP/MameBIHPrGWmp1ctA73vAz1vqJDBte/HMskqHXp9gIv7Ub3tXWx/aBLuDIh3ASKShJCkmSgAJebTzgBX0lYiMfPGq3OvyxHx/xHx9sZ9wBzY4+G2SDKz7I47X2yBpXWhtk8eJDzW9kY6MT2P/q0FeAvprkO3Yj
What is y - 3 = -2(x - 2)
OR
y + 2 = -2(x + 0)
The number of solutions to the following system of equations:
3x - y = 12
y = 3x - 12
What is infinitely many?
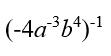 in simplest form
in simplest form
What is - a3/4b4
The factored form of a2 - 3a - 54
What is (a - 9)(a + 6)?
What is 136?
The equation of a line that passes through (2, 4) and (-2, 6) in slope-intercept form
2/-3
What is y = -1/2 x + 5?
Whether (2, -1) is part of the solution to:
3 - 3y < 3x
3y > 2x + 1
What is no?
The product of
(n + 4)(3n - 5)(n - 6)
What is 3n3 - 11n2 - 62n + 120?
The factored form of 2r3 - 24r2 - 5r + 60
What is (2r2 - 5)(r - 12)?
The number of roots to an quadratic that is a perfect square trinomial
What is one?
The equation of a line that is perpendicular to y = 2/5x - 4 and passes through the point (4, 1)
What is y = -5/2 x + 11?
Two solutions to the system of inequalities below
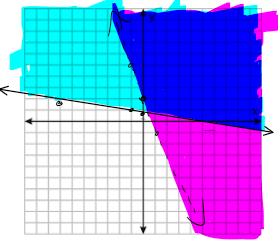
What is ANSWERS WILL VARY
The reason (x + 4y)3 is not equal to x3 + 64y3
What is you cannot distribute the exponent because the expression in the parentheses is bound by addition, therefore by distributing you are missing 6/8 partial products?
4n4 - 29n2 + 25 factored completely
What is (n -1)(n + 1)(2n + 5)(2n - 5)?
The solution to
2x2 - 2x + 15 = 0
What is no solution?