Sequences
Multiplying/ Dividing Polynomials
Adding/ Subtracting
End Behavior
Unit Circle
100
Is it geometric, arithmetic, or neither? State the ROC or GF.
-4, 2, -1, 1/2
Geometric
Growth Factor: x* 1/2
100
(x+3)(x+7)
x2+10x+21
100
(4x + 9) +(x - 4)
5x + 5
100
If a polynomial is 2nd degree, the shape of it's graph will be _____.
A parabola, quadratic.
100
135º in radians
3/4π
200
Is it geometric, arithmetic, or neither? State the ROC or GF.
2 1/2 , 3, 3 1/2, 4, 4 1/2...
Arithmetic
Rate of change: +1/2
200
(x+2)(x+4)
x2+6x+8
200
(-3a - 2) + (7a + 5)
4a + 3
200
What do we know about the leading term of this graph?
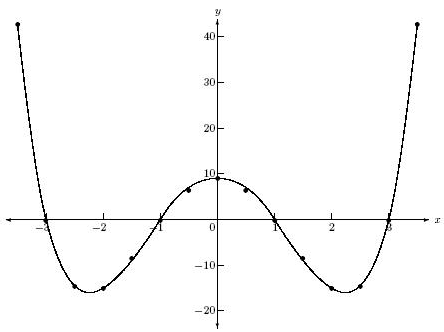
Degree: Even
Leading Coeffcient: Positive
200
210º in radians
7/6π
300
The Growth Factor of the Sequence 2,4, 8, 16,32...
2
300
(7x2+8x+2)(8x2+6x+5)
56x4+106x
300
(k3 + 6k3 -4) - (5k3 + 7k -3k2)
k3 + 4k2 -7k -4
300
Describe End Behavior (using infinity)
As x 
As x
300
13π/6 in degrees
390º
30º
400
Write an equation for the nth term of the geometric sequences.
3, 15, 75, 375, 1875,
f(n) = 3* (5)n for n ≥0
400
Divide:
(x2 - 10x +21) / (x - 3)
(x - 7)
400
(3 - 6x5 - 8x4) - (-6x4 - 3x - 8x5)
2x5 - 2x4 + 3x + 3
400
Describe end behavior (using infinity)
As x
As x
400
5π/3 in degrees
300º
500
Write an equation for the nth term of the arithmetic
sequences. 1, 4, 7, 10, 13, ...
f(n) = 3n -2 for n ≥ 1
500
What is the remainder of this division problem?
x3 - 2x2 + x - 5 / x - 2
- 3
500
(-7x5 + 14 -2x) + (10x4 + 7x + 5x5)
-2x5 + 10x4 +5x + 14
500
Describe the following for the graph:
Leading coefficient, degree, zeros, y intercept
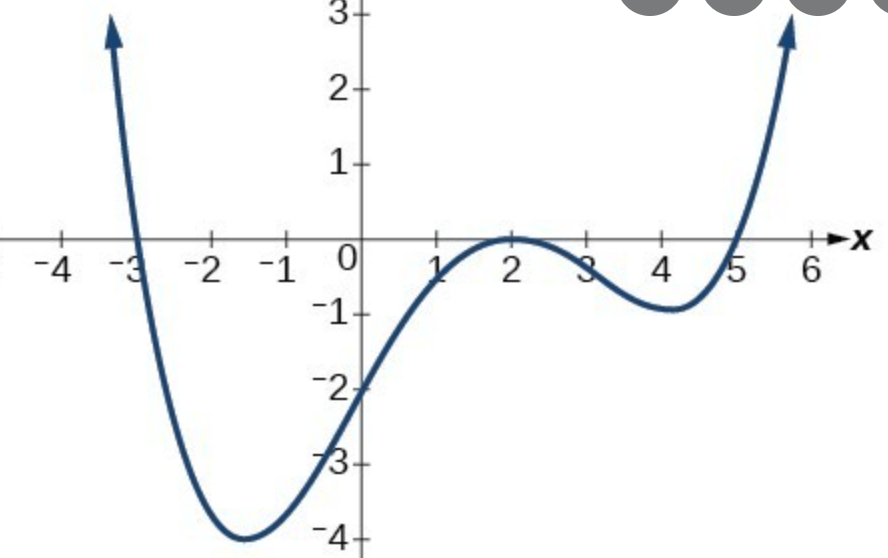
L.C.: positive
Degree: even
Zeros: -3, 2, 5
Y-int: -2
500
405º in radians
9π/4