Simplifying Expressions
Solving Equations
Graphs
Derivatives
Assorted Problems
100
Simplify
\frac{3x+2}{7} - \frac{6-2x}{5}.
Anything equal to
\frac{29x-32}{35}.
100
Solve the following equation for x:
3x - 4 = A.
x = \frac{A + 4}{3}.
100
Sketch the following function:
f(x) = 7x+2.
The line that passes through (0,2) and has slope 7.
100
Evaluate
\frac{d}{dx}(4x^2-5x+2).
8x-5.
100
Suppose a circle has a diameter of 25 meters. What is the circumference of this circle?
25pi
meters.
200
Simplify
\frac{(2x^2)^3\cdot y^2}{y^5\sqrt{x^4}}.
Anything equal to
\frac{8x^4}{y^3}.
200
Solve the following equation for x:
x^2 + x = 6.
x=2,x=-3.
200
Give an equation of a concave up parabola with vertex (5,-10).
y = A(x-5)^2-10,
where A is positive.
200
Evaluate
\frac{d}{dx}(\frac{3}{5}x^5 - e^{35x} + 2x).
3x^4 - 35e^{35x} + 2.
200
Let
theta = \frac{2\pi}{3}.
Evaluate:
\sin(\theta),\cos(\theta),\tan(\theta).
\sin(\theta) = \frac{\sqrt{3}}{2},\cos(\theta)=-\frac{1}{2},\tan(\theta)=-\sqrt{3}.
300
Simplify
log_7(\frac{7^{2(x-3)}\sqrt{7}}{7^{\frac{3}{2}-x}}).
Anything equal to
3x-7.
300
Solve the following equation for x:
4e^{13x+2}-5e^{7x-2}=2e^{7x-2}-10e^{13x+2}.
x = \frac{ln(1/2)-4}{6}.
300
Find an equation of a sine graph with a maximum value of 20, with a frequency of 1/5, with a phase shift of 0.5, and with a bias of 15.
y=5sin(2pi(\frac{1}{5}x-0.5))+15.
300
Suppose
f(x) = 3x^2 + 5.
Evaluate
\frac{f(x+h)-f(x)}{h}.
6x+3h.
300
Is \frac{2x}{2x+2y} always equal to \frac{x}{x+y} ? Justify verbally.
Yes
400
Simplify
(2cos(x))^2 + (3sin(x))^2.
Anything equal to
4+5sin^2(x).
400
Solve the following equation for x:
log_2(x + 4) + log_2(x-3) = 3.
x=4.
400
Turn the equation
y = 5x^3
into log form. Is the equation log-log or semi-log?
The log form of the equation is
log(y) = log(5) + 3log(x).
The equation is log-log.
400
Suppose
f(x) = \frac{1}{3}x^3 - 6x^2.
Find real numbers such that
f'(c) = -32.
c=4,c=8.
400
Suppose f(x)=\frac{6+15e^x}{3+5e^x} . Find lim_{x\to\infty} f(x), lim_{x\to-\infty} f(x), and f(0)
lim_{x\to\infty} f(x) = 3, lim_{x\to-\infty} f(x) = 2, f(0)=21/8
500
Simpify
\frac{tan(2x)(cos(x)-sin(x))}{4cos(x)sin(x)}.
Anything equal to
\frac{1}{2(cos(x)+sin(x))}.
500
Solve the following equation for x:
10sin^2(x) = 5.
x = \frac{pi}{4} + 2pik,x = \frac{3pi}{4} + 2pik,
x = \frac{5pi}{4} + 2pik, x = \frac{7pi}{4}+2pik.
500
Which equation most closely matches this graph:
(a) \frac{4+8e^x}{2+2e^x}
(b) \frac{8+24e^x}{2+3e^x}
(c) 8e^{x/2}
(d) 8^x-4^x
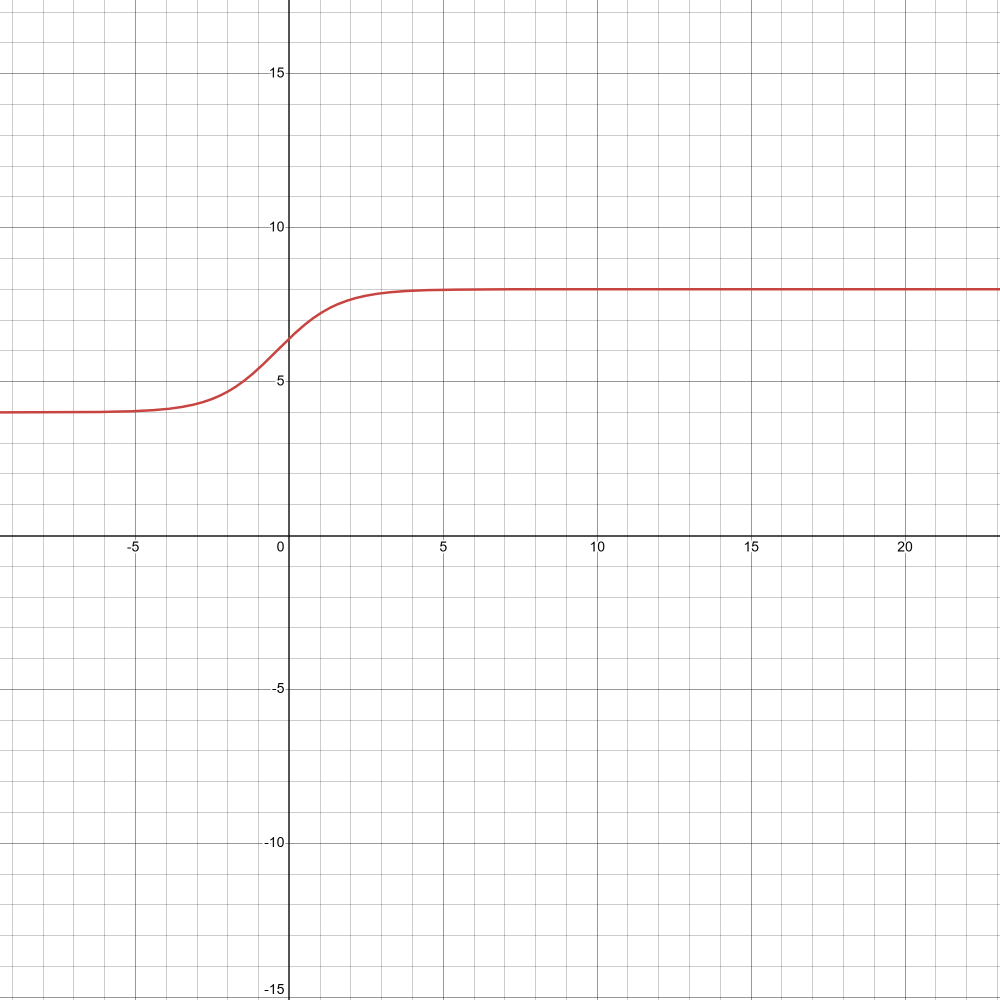
\frac{8+24e^x}{2+3e^x}
500
Suppose
f(x) = 2\sqrt{x} + 5.
Evaluate
\frac{f(x+h)-f(x)}{h}.
\frac{2}{\sqrt{x+h}+\sqrt{x}}.
500
Let
f(x,y) = x^2 + y^2 + 5
and let
g(x) = \frac{1}{\sqrt{x}}.
Evaluate
g(f(\sqrt{12},\sqrt{8})).
\frac{1}{5}.