Factoring
Equations
Graphing/Equations of Lines
Expressions
Word Problems
100
2x^2+19x+24
(2x+3)(x+8)
100
Solve by completing the square:
x^2+16x=-15
x=-1,-15
100
Write an equation for a line that passes through (6, 1) and (-4, 3).
y=-1/5x+11/5
100
4sqrt2(2sqrt6-6sqrt3)
16sqrt3-24sqrt6
100
Victoria left home and drove toward the city. Cecelia left one hour later driving at 80 mph in an effort to catch up to Victoria. After driving for three hours Cecelia finally caught up. What was Victoria's average speed?
60 mph
200
12x^2+69x+45
3(4x+3)(x+5)
200
5x-6y=2
4y-5x=12
(-8,-7)
200
Write an equation for a line that is parallel to x-y=5 and passes through (3, 3).
y=x
200
sqrt(x^2+8x+16)
x+4
200
Shelby left school and drove east at an average speed of 24 km/h. Kenaan left one hour later and drove in the same direction but with an average speed of 30 km/h. How long did Shelby drive before Kenaan caught up?
5 hours
300
4x^2-13x+10
(4x-5)(x-2)
300
-2x^2+13x=15
x=5, 3/2
300
Give the equation of the parent function:
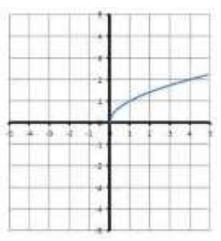
y=sqrtx
300
(12sqrt20)/(4sqrt(3))
2sqrt15
300
Attendance at a football game was 350. Tickets for adults cost $2.25, while student tickets cost $1.00. If the total receipts were $600, how many students and adults attended the game?
150 students
200 adults
400
2x^3+x^2-50x-25
(2x+1)(x+5)(x-5)
400
2x^2-128=0
x= +-8
400
Find the vertex of:
2x^2+4x-6
(-1, -8)
400
6/(3+sqrt3)
3-sqrt3
400
Keegan left the airport and drove north at an average speed of 40 km/h. Jayden left one hour later and drove in the opposite direction with an average speed of 60 km/h. How long does Keegan need to drive before they are 240 km apart?
3 hours
500
6x^4-96
6(x-2)(x+2)(x^2+4)
500
Solve with Quadratic Formula (*Round to nearest tenth):
6x^2-12x+1=0
x=1.9, 0.1
500
Find the vertex of:
-3x^2-6x+4
(-1, 7)
500
(x+2)/(x+4)+1/(x-2)+3
(4x^2+3x-16)/((x+4)(x-2))
500
A freight train left Nashville traveling south 10 hours before a passenger train. The passenger train traveled in the opposite direction going 40 km/h faster than the freight train for 4 hours after which time the trains were 790 km apart. What was the freight train's speed?
35 km/h