Quadratics
Regression
Mix
Chapter 1
Chapter 3
100
Solve using quadratic formula
x^2-3x=9
x = 4.9
x = -1.9
100
What are the steps to complete a linear regression? an exponential regression?
1. STAT
2. Edit
3. Clear out L1 and L2
4. STAT --> CALC: LinReg(ax+b) OR ExpReg
5. Enter until results show up. Substitute values into equation form.
100
Solve using your calculator
x(6x+1) = 15
x = -1.7
x = 1.5
100
What are the three parts to the definition of a function?
1. Domain
2. Range
3. For each input there is exactly one output
100
a. Solve for x: 5x+7 = 18-2x
b. Solve for u:
(uthis)/t = go
x = 11/7
u = (got)/(this)
200
Solve on your calculator
4x^2+4x-8 = 1
x = 1.1
x = -2.1
200
Determine the equation of the line of best fit using linear regression for the following data. Round to the nearest thousandth.
Age: 3 6 9 12 15 18 21
Height: 35 46 51 60 63 75 67
y = 1.976x+33
200
How do you determine if a set of data represents a linear model?
If the two pieces of data have a constant rate of change, then it is linear.
200
Calculate f(3) if
f(x)=3x+1/x
28/3
200
A company manufactures slides. The top of the slide is 5 feet high. The bottom is 7 feet away.
a. Find the slope of the slide.
b. A child complains that the trip down the slide is not fast enough. How should the slope be adjusted to accommodate the unhappy child?
m = 5/7
We can increase the the slope of the slide by either making the "rise" greater or the "run" lesser.
300
Solve using the quadratic equation
9x^2-11=6x
x = 1.5
x = -0.8
300
Perform an exponential equation to find the exponential equation for the data below.
Time: 1 5 8 17 18
Temperature: 43.7 35.2 30 20.1 14.3
y = 47.16(.94)^x
300
The exponential function,
N = 4.013*1.565^y
gives the approximate US population, in millions, y years after 1900.
a. What is the yearly growth factor?
b. What percent does the population grow by each year?
c. Find the year in which the population first exceeds 15 million.
a. 1.565
b. 56.6%
c. 1903
300
Calculate the average rate of change from t=20 and t=30 using the values below. Then use your answer to estimate the value of N(27).
t: 10 20 30 40 50 60 70
N(t): 17.6 23.8 44.6 51.3 53.2 53.7 53.9
rate of change: 2.08
N(36) = 38.36
300
A dairy spends $25,000 per year to maintain its barns and equipment. It costs $2,000 per year to feed and care for each dairy cows.
a. Using C for the number of dairy cows and E for the total yearly expense, in dollars, find a formula that gives thee total yearly expense as a linear function of the number of dairy cows.
b. Use function notation to express the total expense if the dairy has 30 cows.
c. Calculate the value from part b.
a. E = 2000C + 25000
b. E(30) = 2000(30)+25000
c. $85,000
400
Solve using your calculator
x^2+x-4
x = 1.6
x = -2.6
400
Perform a linear regression to find the equation of the line of best fit for the following data.
Miles: 150 200 400 600 1000
Gallons: 7 10 19 29 51
y = 0.05x-.92
400
Solve algebraically
y = 2x+3
y-3x = -4
x = 7
y = 17
400
a. Describe how the value of the Canadian dollar fluctuated from 1990 to 2002.
b. When was the Canadian dollar worth 80 American cents?
c. What was the average yearly decrease in the value of the Canadian dollar from 1992 to 1994?
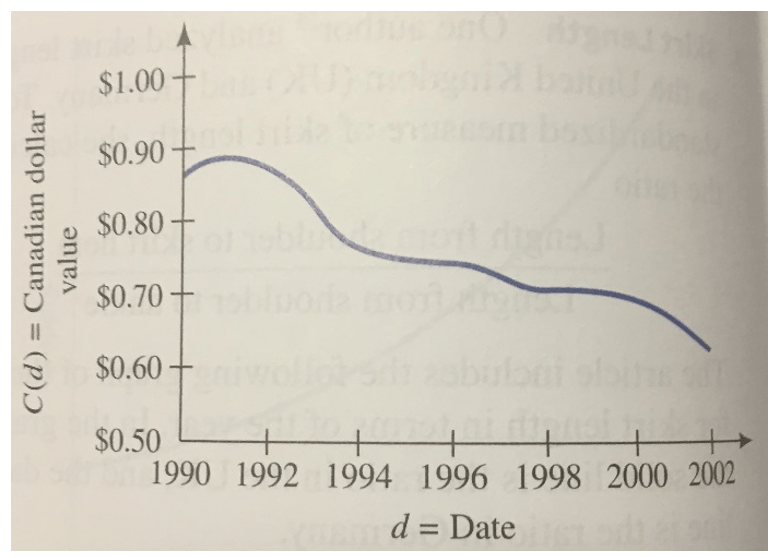
a. Briefly increased before decreasing over time. Peaked around 1991 and bottomed out in 2002.
b. Around 1993
c. Decrease of 5 cents per year
400
a. Show that the data can be modeled by a linear function.
b. Find the slope of the linear function.
c. Find a linear model for the data.
d. Use the result from part c to find the cost to Walmart if employee turnover is 33% in a year.
E: 10 20 30 40
C: 250 400 550 700
a. Rate of change is constant
b. Slope = 15
c. C = 15E+100
d. $595 million
500
Solve using quadratic equation
2x^2-4x-3 = 0
x = 2.6
x = -0.6
500
Find an exponential equation that best represents the data above using exponential regression on your calculator.
Time: 2 4 8 14 20
Depth: 44.7 36.8 29.2 22.3 15.1
y = 47.97(.94)^x
500
Solve algebraically
5y-10x = 20
2y+6x = 38
x = 3
y = 10
500
It takes 10 minutes to preheat your oven to 325 degrees. For an oven preheated to 325 degrees, the recommended cooking time for a turkey is about 15 minutes per pound.
a. Use a formula to express the total time T, in minutes, needed to preheat the oven and then bake a turkey weighing p pounds.
b. Use your formula from part a to find the approximate time required to prepare a turkey weighing 18 pounds.
a. T = 10+15p
b. T = 280 minutes