Transformations
Rotations/Reflection
Translations
Identify Functions
Domain & Range
100
Define the term rigid motion transformations.
A rigid motion transformation preserves the shape and size of the original figure.
100
Are reflections and rotations an example of rigid motion transformations?
Yes, the size and shape are preserved.
100
Define the term translation.
A translation is a geometric transformation that slides a figure to a different location on the coordinate plane.
100
What is the criteria for a relation to be a function?
A function is a type of relation where each input value has exactly one output value.
100
Which variable do we use when describing the domain of a function?
The x, or input, variable
200
Is this a rigid motion transformation?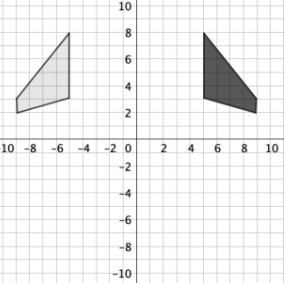
Yes. It is a reflection.
200
What would be the resulting ordered pair if the point (2, 3) were rotated 90° around the origin.
(-3, 2)
200
Describe the movement of the line segment shown by the vector from FG to F'G'
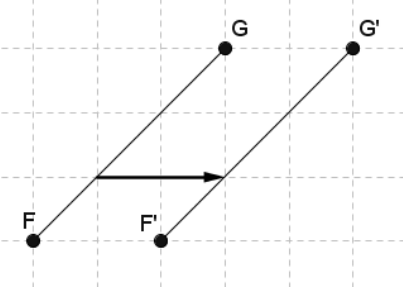
Right 2 units.
200
Is the data set a function? Why or why not?
{(2, 3), (0, 0), (5, 3), (8, –1)}
Yes, this is a function because every input (2, 0, 5, 8) has only one output.
200
Determine the domain and range of the function.
{(1, 3), (2, 7), (8, 1)}
D = {1, 2, 8}, R = {1, 3, 7}
300
Segments A-B and C-D are congruent (identical in shape and size) Describe the transformation to get from A-B to C-D.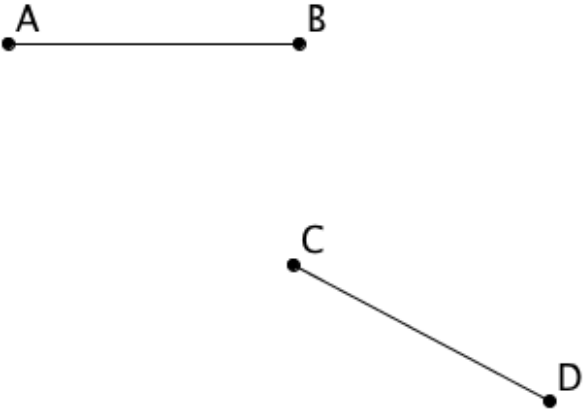
Segment A-B is rotated and translated.
300
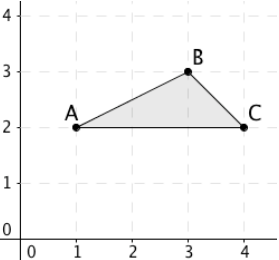If ΔABC were rotated 180° around the origin to
find ΔA’B’C’. Write the resulting points A’, B’, and C’ in the chat.
Resulting points are A’(-1, -2), B’(-3, -3), C’(-4, -2).
300
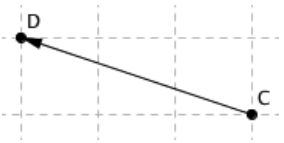Describe the movement the vector shows.
Left 3 units, up 1 unit.
300
Is the graphed relation a function? Justify
your answer.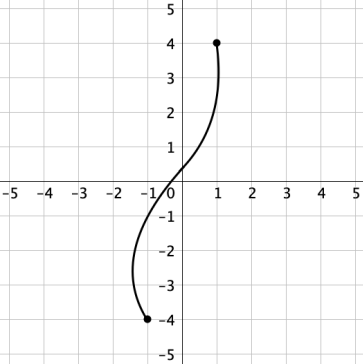
No, the relation is not a function because it does not pass the vertical line test. This means some inputs (like -1) have multiple outputs.
300
State the domain and range of the
function.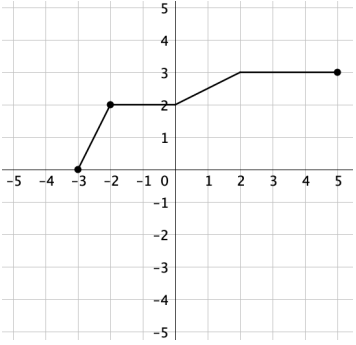
Domain: -3 ≤ x ≤ 5
Range: 0 ≤ y ≤ 3
400
Diego says every segment is a transformation of every other segment. Do you agree with him? Why or why not?
Agree because we can transform between every pair of segments using a combination of the 4 transformations – rotation., dilation, translation, reflection.
400
Define the term reflective symmetry.
A figure has reflective symmetry if half of the figure is a mirror image of the other half.
400
Triangle F′G′H′ is the image of triangle FGH after it was translated 1 unit to the right and 4 units up. What were the coordinates of point F before the translation? A. (2, 7) B. (4, 5) C. (-1, 0) D. (2, -3)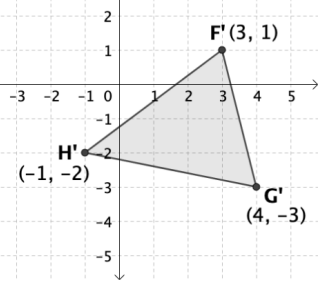
D. (2, -3)
400
Describe the what the vertical line test is and does.
The Vertical Line Test is used to determine if a relation on a graph is a function. A relation is a function if it intersects all possible vertical lines no more than once.
400
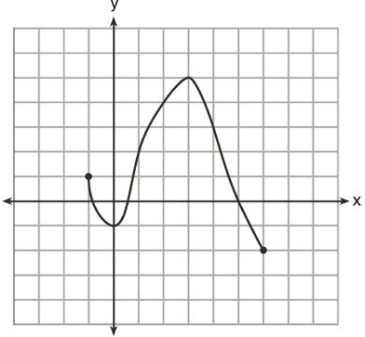Find the domain and range of the function
graphed below.
Domain: {-1≤ x ≤ 6}, Range: {-2 ≤ y ≤ 5}
500
Diego says every triangle is a transformation of every other triangle. Do you agree with him? Why or why not?
No, transformations do not change the shape of an object. Different triangles can have different angles, which means they have different shapes.
500
Describe rotational symmetry.
Rotational symmetry means an object looks the same after it is rotated/turned around a center point by a given measure, called the degree of rotation.
500
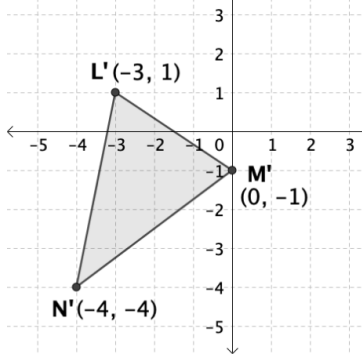Triangle L’M’N’ is the image of LMN after it was translated 2 units left and 3 units down. What are the coordinates of point L?
A. (-1, 4) B. (-5, 4) C. (-1, -2) D. (-5, -2)
A. (-1, 4)
500
Explain why the following graph represents a
function.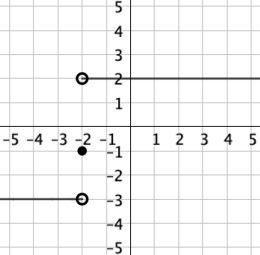
The graph is a function because it passes the vertical line test and each x-value has only one y-value associated with it. There may be confusion at x = –2, but at y = –3 and y = 2, the circles are open, meaning the value is not included in the relation.
500
The function, f(x) = x – 4, is defined on the domain 4 < x ≤ 10. Which of the following would be part of the range? Select all that apply.
A) 5 B) -4 C) 2.5 D) 0 E) 0.5
A) 5, C) 2.5, and E) 0.5