Parent Functions
Translations
Reflections, Stretches and Compressions
Mixed
Mixed
100
Name the parent function.
f(x)=\sqrt { x+3 } -7
Square Root Function
100
Describe the translation.
f(x)=x-4
Shift Down 4
100
Name the transformation.
f(x)=2x^2
Stretch vertically by a factor of 2.
100
Name the transformations.
f(x)=(x-2)^2+5
Shift right 2, up 5
100
Name the transformations.
f(x)=2|x+12|
Vertical stretch by a factor of 2, horizontal shift left 12.
200
Name the parent function.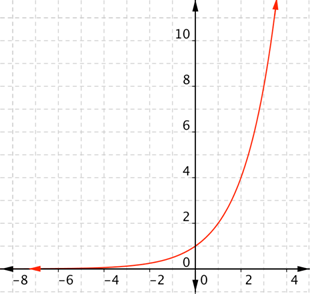
Exponential
200
Describe the translation.
f(x)=(x-2)^2+4
Shift Right 2 and Up 4
200
Name the transformation.
f(x)=|3x|
Horizontal shrink by a factor of 3.
200
Name the transformations.
f(x)=2(x-1)^2
Vertical stretch by a factor of 2, horizontal shift right 1
200
Name the transformations.
f(x)=(2/3x)^2+1
Horizontal stretch by a factor of 3/2, vertical shift up 1.
300
Name the parent function.
f(x)=\sqrt [ 3 -x] -4
Square Root Function
300
Describe the translation.
f(x)=log(x+2)
Shift Left 2
300
Name the transformation.
f(x)=-2|x|
Reflection over the x-axis and vertical stretch by a factor of 2.
300
Describe the transformations.
f(x)=-1/4x^2-6
Reflection over the x-axis, vertical shrink by a factor of 4, and vertical shift down 6.
300
Name the transformations.
f(x)=1/4(x-1)^3-5/2
Vertical shrink by a factor of 1/4, horizontal shift right 1, vertical shift down 5/2
400
Name the parent function.
Reciprocal Function
400
Describe the translation.
f(x)=|x-1/2|+0.75
Shift Right 1/2 and Up 0.75
400
Name the transformation.
f(x)=-|1/2x|
Reflection over the x-axis and horizontal stretch by a factor of 2.
400
Name the transformations.
f(x)=2sqrt(2x)-9
Vertical stretch by a factor of 2, horizontal shrink by a factor of 2, and vertical shift down 9.
400
Name the transformations.
f(x)=2sin(x-60)
Vertical stretch by a factor of 2, shift right by 60.
500
Name the parent function.
f(x)=\frac { 1 }{ 2 } x+7
Linear Function
500
Describe the translation.
f(x)=3^(x-4)+7
Shift Right 4 and Up 7
500
Name the transformations.
f(x)=2(-1/3x)^2
Vertical stretch by a factor of 2. Reflection over the y-axis and horizontal stretch by a factor of 3.
500
Name the transformations.
f(x)=1/5log(3/4x)-8
Vertical shrink by a factor of 5, horizontal stretch by a factor of 4/3, and a vertical shift down 8.
500
Name the transformations.
f(x)=-(3x-6)3+ 8
Reflection over the x-axis, Horizontal compression by a factor of 3, Horizontal shift right 2, vertical shift up 2.