Vocabulary
Is it linear or nonlinear?
Rate of change and Initial Value
Graphing
Is it a Function?
100
y=3x
Linear, in the form y=mx
100
Is it a function? Justify your answer.
{(2, 3), (4, 5), ( -2, 6)}
Yes, each input has exactly one output.
200
Which variable is the input, and which one is the output?
(Which one is the x-variable, which one is the y-variable?)
x-variable is the input, y-variable is the output
(x - independent, y - dependent)
200
y=-5x-4
Linear, in the form y=mx+b
200
Using the vertical line test, does the graph of the points (1,3) and (1,5) represent a function?
No, the points fail the Vertical Line Test.
300
What is the test to tell if a graph is a function?
Vertical Line Test
300
y=x^2
NonLinear (has an exponent)
300
Is it a function? Justify your answer.
| x | y |
| 2 | 4 |
| 1 | 5 |
| 2 | 6 |
No, the input of 2 has two different outputs.
400
What is the definition of a function?
A relationship between input and output values. Each input has exactly one output value.
400
y=5
Horizontal LINE through 5 on the y axis.
400
Which function has the greatest initial value?
Function A
x: 0 2 4 6
y: 0 5 10 15
Function B
y=3x-1
Function C
Function C
400
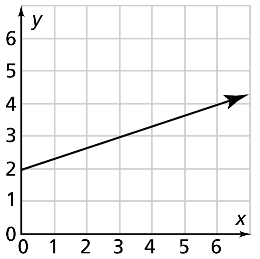
Is the function shown linear or nonlinear? Explain.
The function is nonlinear and does not have a constant rate of change.
400
Is it a function? Justify your answer.
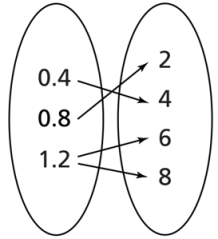
Is the relation shown in the arrow diagram a function? Justify your answer.
No. The input 1.2 has 2 outputs.
500
Is every relation also a function? Explain.
No. A function is a special type of relation where each input maps to exactly one output. In a relation, an input can have one or more outputs.
500
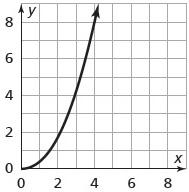
y=square root of x
nonlinear (we did this in class, it had a curve to it)
500
Two linear functions are shown below. What are the rates of change of each functions, and which function has the greater rate of change?
Function A:
x: 0 4 8 12
y: 1 2 3 4
Function B:
y = 0.75x – 2
Function A: rate of change= 1/4
Function B: rate of change= 0.75 or 3/4
Function B has a greater rate of change.
500
Graph this table:
x: 2 4 8 10
y: 3 2 0 -1
Is this a function? Is it linear or nonlinear?
Yes it is a function. It is linear.
500
Is it a function? Justify your answer.
Yes, each input has exactly one output.