Expressions de f et calculs d'images/antécédents
Calculs de limites
Calculs de dérivées
Sur les Extrema
Random
100
Soit
f(x)=(4x-1)*ln(x)
Calculez : f(1)
f(1)=0
100
lim_(x->0+) 1/x =
lim_(x->0+) 1/x=+oo
100
Calculez la dérivée de f(x)=x^3+2x²-x-7
f'(x)=3x²+4x-1
100
La fonction f suivante admet-elle un (ou plusieurs) extremum(a) ? Si oui, donnez leur type.
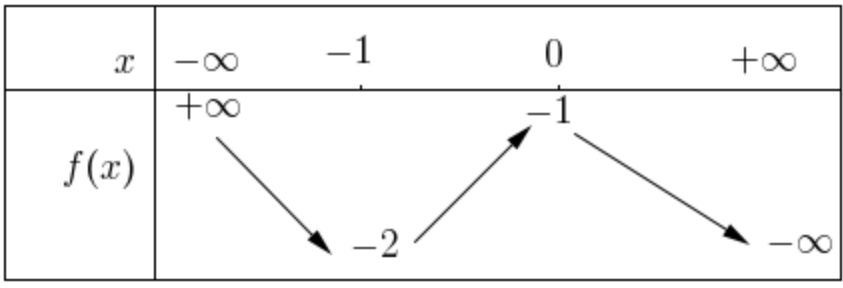
2 extrema : un minimum et un maximum.
(extra : minimum qui vaut -2 atteint en -1 & maximum qui vaut -1 atteint en 0).
100
Est-ce que l'affirmation suivante est vraie ? sin(2pi)=-sin(0)
Oui, les deux sont égales à 0, donc aussi à -0.
200
Donnez l'expression de f(x) qui décrit le problème suivant :
Pam a 135 € sur son compte bancaire et ajoute 45 € chaque mois pour économiser pour un nouveau vélo.
f(x) = 135 + 45x
200
lim_(x->-oo) e^x=
lim_(x->-oo) e^x=0
200
Calculez la dérivée de f(x)=e^x+x^7+1/x
f(x)=e^x+7x^6-1/(x²)
200
La fonction suivante admet-elle un(des) extremum(a) ?
Si oui, donnez leur nature, leur valeur et en quel point ils sont atteint.
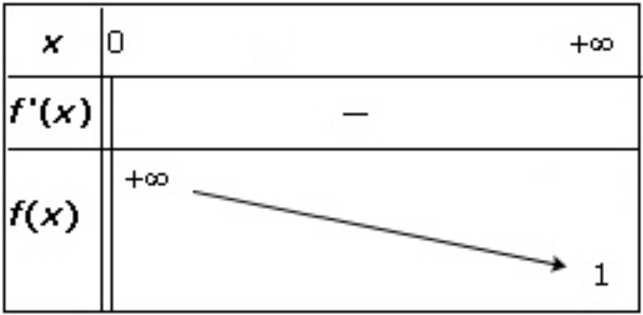
Il y a pas d'extremum local.
(extra : il y a deux asymptotes, une horizontale et une verticale)
200
La fonction e^x admet une asymptote horizontale en - oo d'équation :
y=0
300
Calculez P(-4) si
P(x)=-5x² + 2
P(-4)=-78
300
lim_(x->-oo) ln(x)
lim_(x->-oo) ln(x)
n'existe pas !
300
Calculez la dérivée de f(x)=(x²+1)*(4x-2)
f'(x)=2x*(4x-2)+(x²+1)*4
=8x²-4x+4x²+4
=12x²-4x+4
300
Si la fonction suivante admet des extrema locaux, donnez leur nature, leur valeur et en quel point ils seraient atteints.
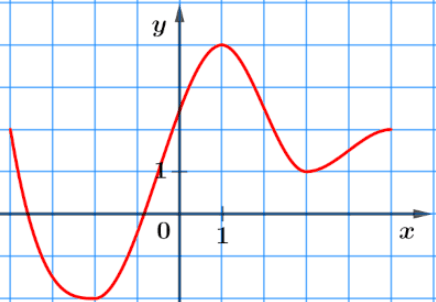
3 extrema locaux :
1 maximum qui vaut 4 atteint en 1.
1 minimum qui vaut -2 atteint en -2.
1 autre minimum qui vaut 1 atteint en 3.
300
Sur quel intervalle la fonction f suivante est-elle croissante ?
f(x)=(x²-1)^3
f'(x)=3*2x*(x²-1)²=6x(x²-1)²
f'(x)>0 quand 6x>0 donc f est croissante sur l'intervalle
[0;+oo]
400
Résoudre : f(x)=0 quand f(x)=x²+3x+2
On a delta=1
donc
x1=-2
et
x2=-1
400
lim_(x->+oo) ln(x)/x=
lim_(x->+oo) ln(x)/x=0
400
Calculez la dérivée de f(x)=(x²+1)/(4x-2)
f'(x)=(2x*(4x-2)-(x²+1)*4)/((4x-2)²)
=(8x²-4x-4x²-4)/((4x-2)²)
=(4x²-4x-4)/((4x-2)²)
400
Si la fonction suivante admet des extrema locaux, donnez leur nature, leur valeur et en quel point ils seraient atteints.
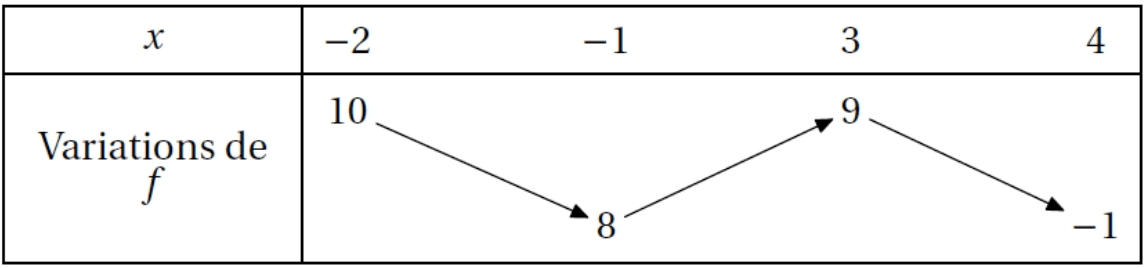
Attention, il n'y a pas d'extrema en -2 ni en 4, car on ne sait pas si la dérivée change de signe en ces points.
Donc les deux seuls extrema locaux connus :
- 1 minimum qui vaut 8 atteint de -1.
- 1 maximum qui vaut 9 atteint de 3.
400
Quelle est l'équation de la tangente à la courbe de f au point d'abscisse 1 si f(x)=1/x
y=-x+2
500
Résoudre : ln(x)+1=0
e^(-1)
500
Soit f(x)=(2x²)/(1-x)
Calculez lim_(x->1^-) f(x)=
lim_(x->1^-) f(x)=+oo
500
Calculez la dérivée de f(x)=e^(-2x+6)
Et donnez son signe sur |R.
f'(x)=-2e^(-2x+6)
e^(-2x+6)>0
pour tout x donc
f'(x)<0
pour tout x. (car -2<0)
500
(2 min) Donnez la ou les bonnes réponses :
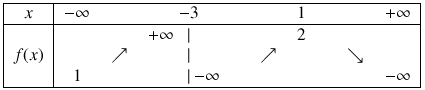
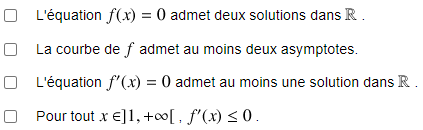
Toutes les réponses étaient bonnes.
500
(1min30)
Quelle est l'équation de la tangente de f au point 1 si f(x)=xln(x)
y=x-1