Find the inverse of this relation;
(0, 2) (5, 10) (7, 25) (8, 30) (10, 45)
(2, 0) (10, 5) (25, 7) (8, 30) (45, 10)
Write a piecewise function for
f(x) = 2|x| - 5
without using absolute value.
-2x - 5 x<=0
2x-5 x>0
Describe the transformations of the parent function:
g(x) = |x - 4| - 3
down 3, right 4
f(x) = x2 - 3
g(x) = 2x - 1
solve f(x) + g(x)
x2 + 2x - 4
Find the inverse of this function;
f(x) = 2x - 7
0.5x +3.5
Write a transformation for the piecewise function down by 5:

x - 2
-|x|
x - 9
Given f(x) = 2 + √(x),
write a rule for g(x), where g(x) is a vertical stretch by a factor of 3 and a translation to the right by 1.
4 + 2√(x+1)
f(x) = x2 - 3
g(x) = 2x - 1
Solve 2f(x) - g(x)
2x2 - 2x - 5
Are these functions inverses?
f(x) = 5x + 10
g(x) = 1/5x - 10
no
Evaluate:
150
Transform the function to the left by 5.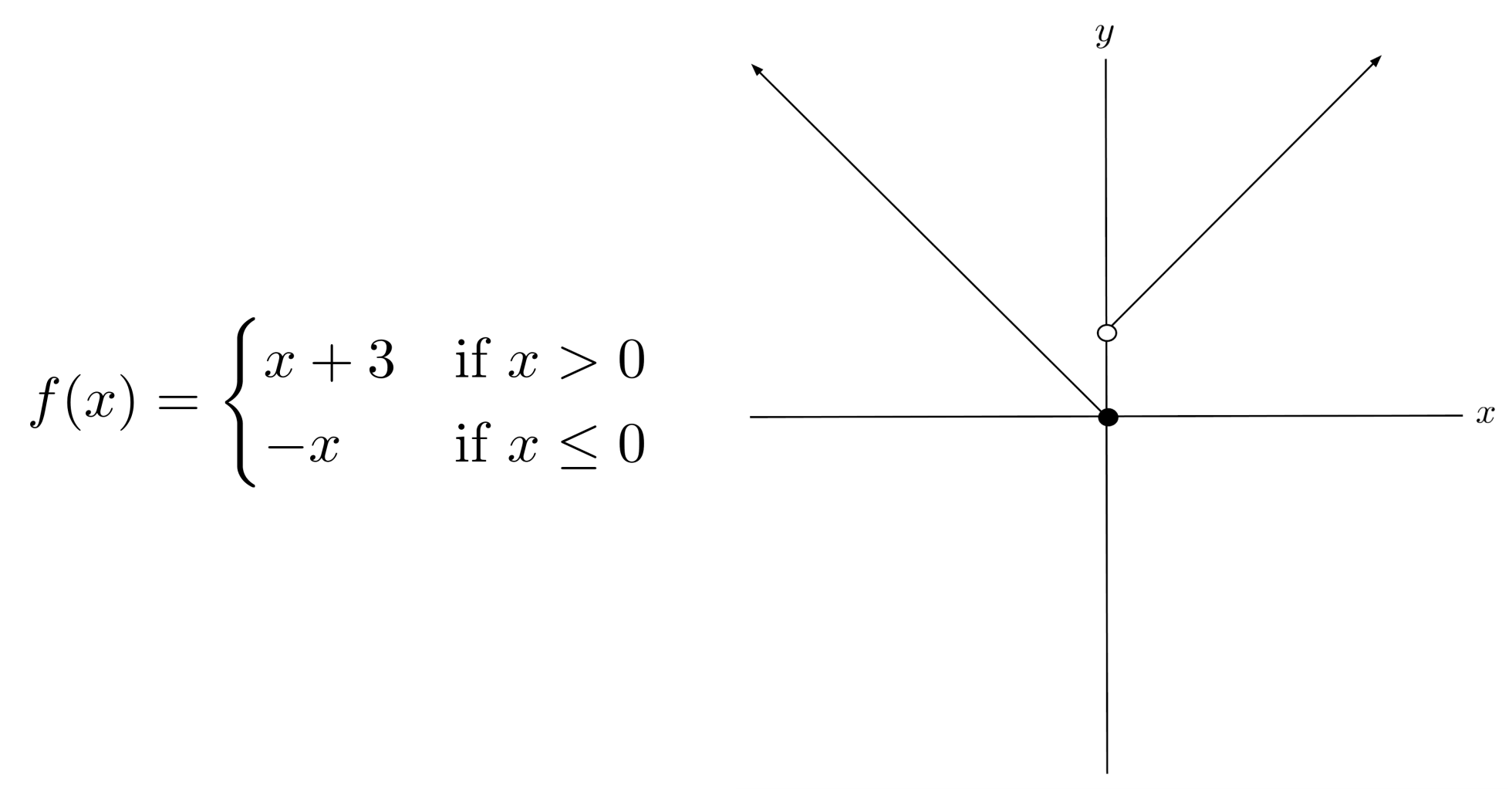
x + 8 if x>-5
-x + 5 if x<=-5
f(x) = x2 - 3
g(x) = 2x - 1
Determine f(g(-3))
46
Determine the domain and range of the inverse, f-1(x):
f(x) = √(x-4)
D; x>=0
R; y>=-4
Write a piecewise function for the graph:
*
f(x) = -(x+3)3
Describe the transformations on f(x) on the parent function.
Left 3, reflected over the x-axis
f(x) = x2 - 3
g(x) = 2x - 1
determine f(g(x))
4x2 - 4x -2
Determine the inverse;
f(x) = 5/(x+3) - 4
f-1(x) = 5/(x+4) - 3
Write the piecewise function
-x2 + 2 if -2 < x < 1
√x if x > 1
The function:
f(x) = x2 - 3
Undergoes the transformation:
g(x) = f(1/2x + 2)
What is the resulting function g(f(x))?
g(x) = 1/4x2 + 2x + 1
f(x) = x2 - 3
g(x) = 2x - 1
Determine f(g(x + 1) - 2)
4x2 - 5


