Graphs
Domain
Range
Random
Functions?
100
In which quadrant is both y and x positive?
Quadrant 1
100
What is the domain of the following set of ordered pairs?
{(2, 1) (-1, 0) (-1, 3) (0, 2) (-5, 1)}
{-5, -1, 0, 2}
100
What is the range of the following set of ordered pairs?
{(2, 1) (-1, 0) (-1, 3) (0, 2) (-5, 1)}
{0, 1, 2, 3}
100
What is the value of g(10) when g(x)=5x+3 ?
53
100
Draw three DIFFERENT graphs that represent a function
Must pass the VLT
200
In which quadrant is point (-3,-6)
Quadrant 3
200
What is the domain of the following arrow diagram?
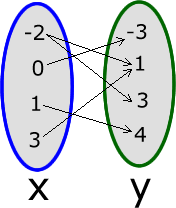
{-2,0,1,3}
200
What is the range of the following set of ordered pairs?
{-3, 1, 3, 4}
200
True or False?
The function g has a domain of {2,4,6,8} and a range of {3,5,7}.Could g be represented by the set of ordered pairs {(2,3),(4,5),(6,7),(8,3)} Justify your answer.
True, ranges can repeat and still represent a function.
200
Draw three DIFFERENT graphs that are NOT functions
Must fail the VLT
300
Is the following set of ordered pairs a function? Why or why not?
{(0, 1) (0, 2) (0, 0) (0, -2) (0, -8)}
No - not a function. Because we have multiple x-values that have the same y-value. Does not pass the vertical line test.
300
What is the domain of the following set of ordered pairs?
(-2, 1) , (4, 5) , (9, -1) , (-3, 0)
{-3,-2, 4, 9}
300
What is the range of the following set of ordered pairs?
(-2, 1) , (4, 5) , (9, -1) , (-3, 0)
{-1, 0, 1, 5}
300
What is the value of h(12)when h(x)=2x−4?
20
300
Given the relation {(5,1),(2,4),(9,3),(m,6)}, which value of m will result in the relation not being a function? LIST ALL POSSIBLE VALUES.
m=5
m=2
m=9
400
What ordered pair corresponds to the green point?
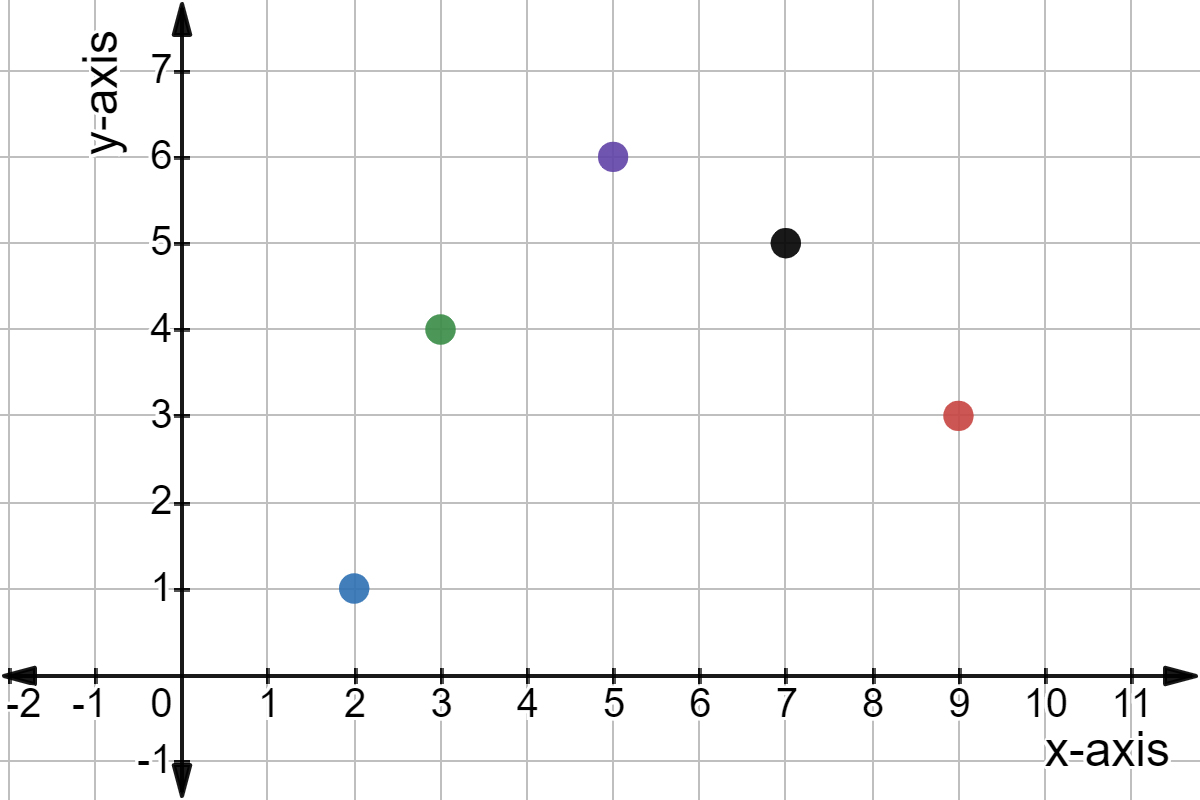
(3,4)
400
What is the domain of the following set of ordered pairs?
(0, 3), (0, 2), (0, 0), (0, 1)
{0}
400
What is the range of the following set of ordered pairs?
(0, 3), (0, 2), (0, 0), (0, 1)
{0, 1, 2, 3}
400
What are 4 ways of representing a relation?
words, graphs, equations, ordered pairs, matching/arrow diagram, table of values (TOV)
400
Which set of ordered pairs represents a function?
A) {(1,2),(2,3),(3,4),(1,5)}
B) {(4,5),(4,6),(7,8)}
C) {(2,3),(3,4),(5,6)}
D) {(0,1),(1,2),(1,3)}
C) {(2,3),(3,4),(5,6)}
500
Is this graph discrete or continuous? Why?
Discrete. There are no lines between the points.
500
Officials in a city use a function T(m) to analyze pedestrian traffic at a crosswalk, where m represents the number of pedestrians observed in a specified time interval. What would be the most appropriate domain for the function T(m)?
{ 0,1,2,3....}
500
Let g be a function such that g(x)= 3x + 1 is defined on the domain 1 ≤ x ≤ 5. What is the range of this function?
4 ≤ x ≤ 16
500
When examining a graph to find the domain we look _____ to _____.
When examining a graph to find the range we look ____ to ______.
left to write.
top to bottom.
500
Anthony is constructing a table of values. What number can be placed in the empty cell so that the table still satisfies the definition of a function?
Input: Output:
-1 2
2 4
? -6
-4 28
5 0
Any numbers other than -4,-1,2,5