Give another name for Plane J:
Example: Plane ACD (cannot use ACB since collinear)
Name a pair of vertical angles
angleABD and angleCBG
Write a conditional statement for the following in if-then form:
"Prime numbers greater than 2 must be odd"
If a number is prime and greater than 2, then it must be odd
Name one of the parallel line theorems
Ex: Corresponding angles are congruent when lines parallel.
Based on the diagram, is the following true or false and why?
" angle1congangle5 "

True, since they are vertical angles and vertical angles are always congruent.
Name a pair of opposite rays
CA and CB (include ray line above)
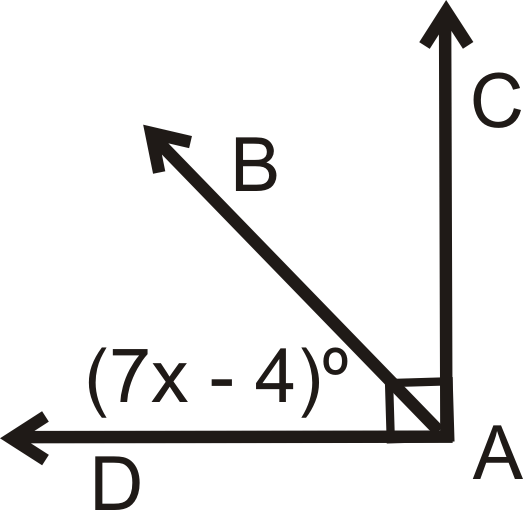
Find the value of x:
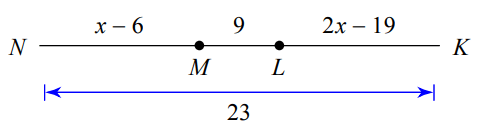
x=13
Make a counterexample to the statement:
"Any two lines cut by a transversal forms congruent corresponding angles"
If the lines are not parallel this is never true (any example of this works)
Find the values of a and b, so that r||s and t||u
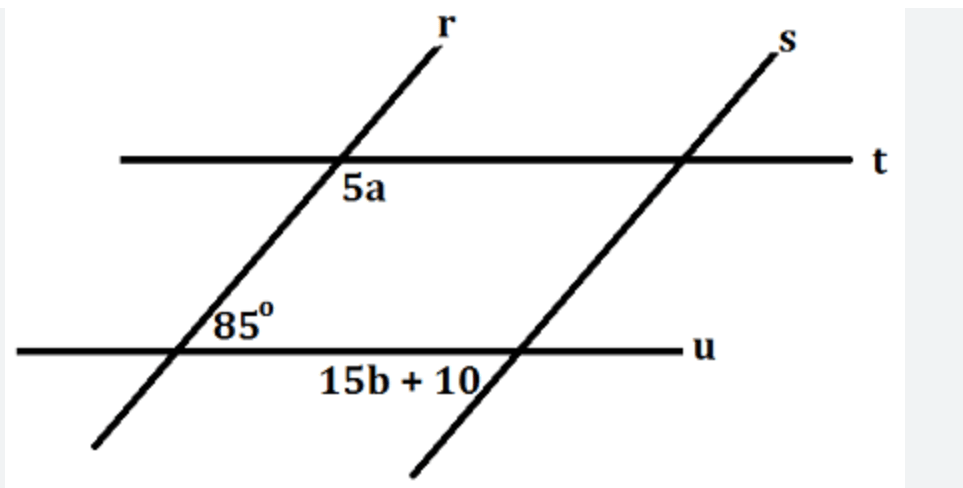
a=95, b=5
Determine if the following is true or false and explain why.
" angle1 supplementary to angle2 "

False, this is only true if n is parallel to m but there are no symbols on the diagram to indicate this.
Would you consider points B,D,G and E to be coplanar? Why or why not.
No they are not coplanar, looking at B,D,G they lie in plane J but E lies off that plane. Therefore they are not coplanar.
List a pair of complementary and a pair of supplementary angles.
Complementary: angleEBF and angleFBC
Supplementary: Any linear pair works here (Ex: angleABF and angleFBC )
Write the converse of the statement and determine if it is never, sometimes, or always true. Explain your answer.
"If a shape is a triangle, then its perimeter is the sum of its sides"
Converse: "If a shape's perimeter is the sum of its sides, then it is a triangle"
Sometimes true, it can be a triangle but it can also be any other polygon as well.
List all angles that angle9 is guaranteed congruent to. State the relationships used to show each congruency.

Angle 11 by Vertical Angles.
Angle 1 since Corresponding Angles Congruent when lines parallel.
Angle 3 since Alternate Interior Angles are congruent when lines parallel
(Note that since p is not parallel q, all bottom angles are off limits"
Determine if the following is true or false and explain why.
"If the bottom triangle is an acute triangle, then the top triangle is also"

False, since the bottom triangle being acute only tells us that the angle between 2 and 3 is acute, this means either of the other angles in the triangle can still be right or obtuse.
Name the intersection of both KF with Plane J and AC with Plane J:
Intersection of KF and Plane J: Point K
Intersection of AC and Plane J: Line AC
Given Ray AB is an angle bisector, find x:
x=7
Make a mathematical statement that when stated as a conditional statement is true but whose converse is not always true.
Many Examples! Here's one:
"A pair of 45 degree angles is complementary"
Find the equation of a line perpendicular to the following line through the point (-27,13).

y=-1/3x+4
Determine if the following statement is true or false and explain why:
"If m parallel n, the following equation is always false mangle1+mangle2+mangle4=180 "

True, since m parallel n this means angle 1 and 2 are supplementary, thus for the given equation to be true we must have
mangle4=0
. Which is not possible!
How many unique planes are in the prism below:
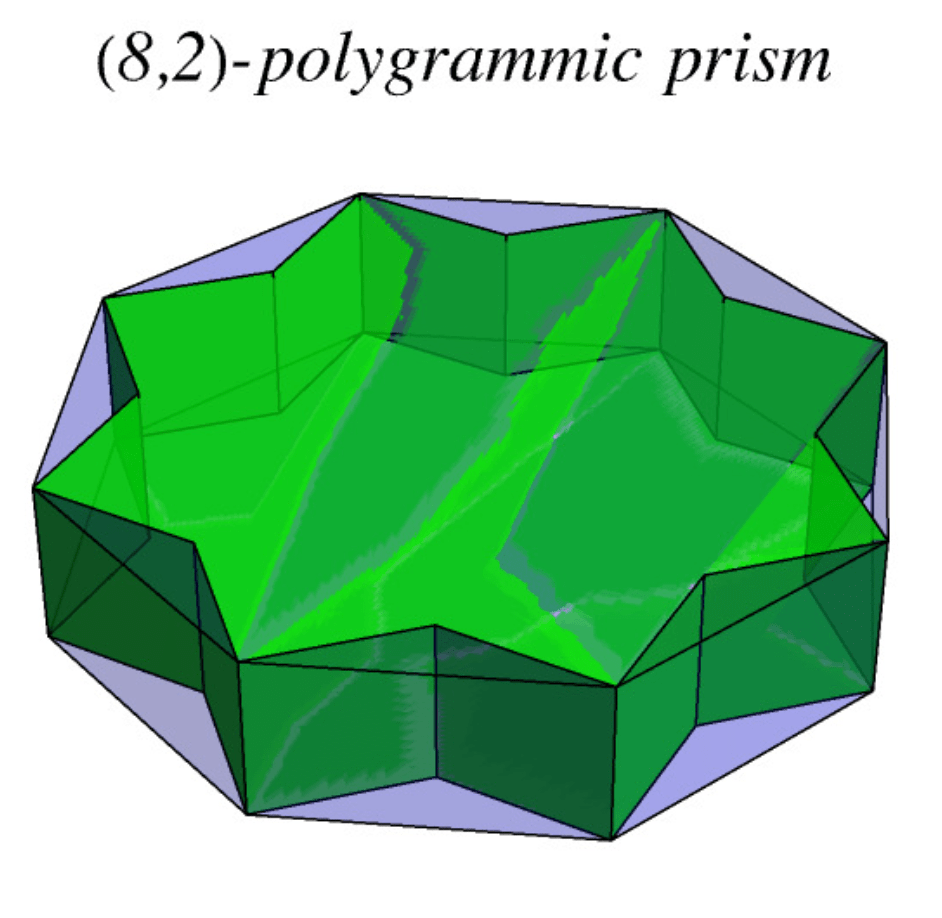
10 unique planes
The value of angle A is 20 less than 3 times the measure of it's linear pair angle B. Find the measure of angle A and angle B
mangleA=130 and mangleB=50
Are the following statements logically equivalent? Explain.
Statement #1: "If a triangle is equilateral, then it has 3 congruent angles"
Statement #2: "If a triangle does not have 3 congruent angles, then the triangle is not equilateral"
Yes they are! Since the first statement tells us any equilateral triangle is equiangular, any triangle that is not equiangular cannot be equilateral!
Statement #2 is called the contrapositive of Statement #1 and its actually always true if the original conditional statement is true!
Find the value of a, b, c, ..., and t (no l, o, or r)

a=64, b=116, c=116, d=64, e=108, f=72, g=108, h=72, i=108, j=108, k=108, m=105, n=79, p=90, q=64, s=108, t=119
Determine if the following is true or false, then explain why.
"It is not possible to have every angle in the diagram be congruent"
False, if u, t, or s is perpendicular to m then all the angles will be 90 degrees (we can show this using various parallel line theorems).