Triangles can be proven congruent by
SAS, SSS, ASA, AAS and HL Theorems
Angles that are opposite and equal
Vertical Angles
The sum of the lengths of two sides of a triangle > the 3rd side
Triangle Inequality Theorem
What is the midpoint formula?
What is the symbol that describes an angle?
∠
Triangles can be proven similar by
AA, SAS and SAS Similarity Theorems
ΔABC is an isosceles triangle. Line segment AB = Line segment AC. If angle B is 75 degrees, what is angle A?
30 degrees
DE=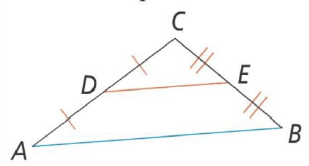
1/2 AB
What is the distance formula?
(Triangle FGH) If Line Segments FG = HG, then ∠H = ∠F
What theorem does this statement show?
Isosceles Triangle Theorem
Theorem which states that the sum of the measures of the angles of triangle = 180 degrees.
Triangle Angle Sum Theorem
Opposite angles in inscribed quadrilaterals are
Supplementary
#4 on Geometry Assessment Handout
Find each line segment length (RS, SQ, RQ) with the following info:
Triangle RSQ is an isosceles triangle.
RQ = x
RS = SQ
RQ = 4
RS = 20
SQ = 20
(0.5, 1.5)
Angles that are adjacent and equal 180 degrees
Supplementary Angles
Theorem which states the measure of an exterior angle of a triangle is equal to the sum of the measures of the two remote interior angles.
Exterior Angle Theorem
Consecutive angles in Parallelograms are
Supplementary
#5 on Geometry Assessment Handout
Yes because a and b are greater than c.
Find distance of (-2,3) and (-7,7).
6.403...
#9 on Geometry Assessment Handout
What is the midpoint of points B(4,-2) and C(0,6)?
(2,2)
(Triangle XYZ) If m<X = m<Y, then Line Segment YZ
cong
line segment XZ.
What theorem does this statement show?
Converse of the Isosceles Triangle Theorem
Sum of angles in any polygon is
(n-2) 180
#6 on Geometry Assessment Handout
12 < c < 52
Because of:
32-20 < c < 32+20
Find distance of (6,4) and (-5,-1).
12.083..
#10 on Geometry Assessment Handout
What is the distance between points P(-2,6) and Q(3,-6)?
13