Lesson 2-1
Lesson 2-2
Lesson 2-3
Lesson 2-4
Lesson 2-5 & 2-6
100
Use inductive reasoning to find the next two numbers.
1,4,2,5,3,6,...
4,7
100
Write the sentence as a conditional statement.
A point in the third quadrant has two negative points.
If a point is in the third quadrant, then it has two negative points.
100
Fill in the blank.
A ___________ is a single true statement that combines a true conditional and its true converse.
Biconditional
100
Fill in the blank.
To use the _________________, identify the hypothesis of the given true conditional. If the second given statement matches the hypothesis of the conditional, then you can make a valid conclusion.
Law of Detachment
100
Name the property of equality or congruence that justifies going from the first statement to the second statement.
ST = QR
QR = ST
Symmetric Property of Equality
200
Find the pattern in this sequence. Use the pattern to show the next two terms.
1,4,9,16,25,...
x^2; 36,49
200
Write the converse from each given biconditional.
A figure is a segment if and only if it is straight and has two endpoints.
If it is straight and has two endpoints, then it is a segment.
200
The conditional statement is true. Write its converse. If the converse is also true, combine the statements as a biconditional.
If two segments have the same length, then they are congruent.
Converse: If two segments are congruent, then they have the same length;true.
Biconditional: Two segments are the same length if and only if they are congruent.
200
Fill in the blank.
___________ allows you to state a conclusion from two true conditional statements when the conclusion of one statement is the hypothesis of the other statement.
Law of Syllogism
200
Use the Transitive Property of Equality to complete the statement.
If <XYZ = <AOB and <AOB=<WYT, then ________________
<XYZ = <WYT
300
Find one counterexample to show that each conjecture is false.
<1 and <2 are a linear pair, so one of the angles is acute.
Two right angles.
300
Write the inverse of the conditional statement.
If two angles share a side, then they are adjacent.
If two angles do not share a side, then they are not adjacent.
300
Write the two statements that form each biconditional.
A polygon is a triangle if and only if it has exactly three sides.
If a polygon is a triangle, then it has exactly three sides.
If it a polygon that has exactly three sides, then it is a triangle.
300
What can you conclude from the given true statements?
If a student gets an A on a final exam, then the student will pass the course.
Tim got an A on the math final exam.
Since Tim got an A on the math final exam then he will pass the course.
300
Find the value of x.
x=20
400
Find the pattern in the sequence. Use the pattern to show the next two terms.
1, -1, 2, -2, 3,...
Add -2, +3, -4, +5...; -3, 4
400
Write the contrapositive of the given conditional statement.
If your temperature is normal, then your temperature is 98.6 degrees Fahrenheit.
If your temperature is not 98.6 degrees Fahrenheit, then your temperature is not normal.
400
Is the statement below a good definition?
A segment is part of a line.
No. A point can be a part of a line.
400
What can you conclude from the given information using the Law of Syllogism?
If a figure is a square, then the figure is a rectangle.
If a figure is a rectangle, then the figure has four sides.
If a figure is a square, then the figure has four sides.
400
Write a proof for the given statement.
Given:
5(x+3)=-4
Prove:
x=-19/5
Proof
500
What conjecture can you make about the sum of the first 30 even numbers?
30*31, or 930
500
Determine if the conditional is true or false. If it is false, find a counterexample.
If you play a sport with a round ball, then you play basketball.
False, you could play baseball.
500
Write the definition as a biconditional.
A penny is worth one cent.
It is a penny if and only if it is worth one cent.
500
Use the Law of Detachment and the Law of Syllogism to make conclusions from the following statement.
If you live in Minneapolis, then you live in Minnesota.
Darrick lives in Minneapolis.
If you live in Minnesota, then you live in the 10,000 lakes state.
Since Darrick lives in Minneapolis, then he lives in the 10,000 lakes state.
500
Write a proof.
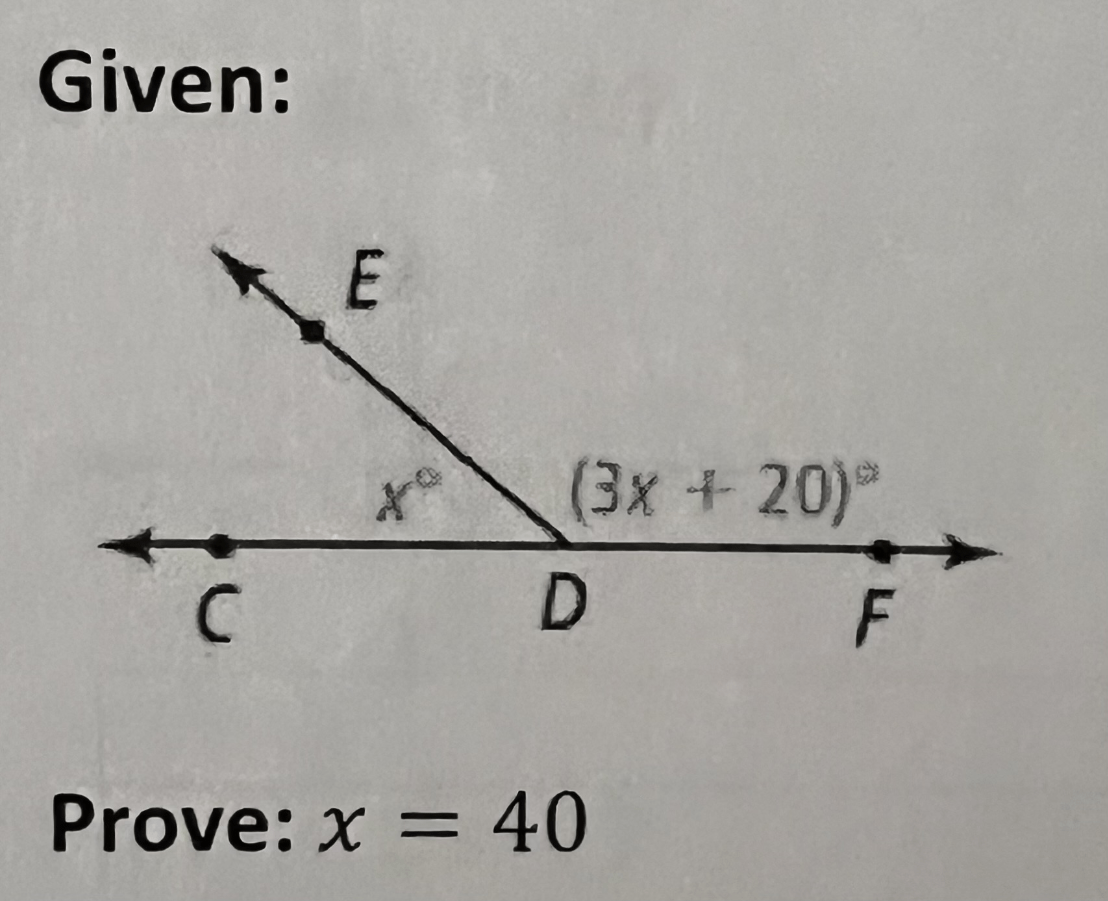
Proof