Any parallelogram with 4 right angles.
Square or Rectangle
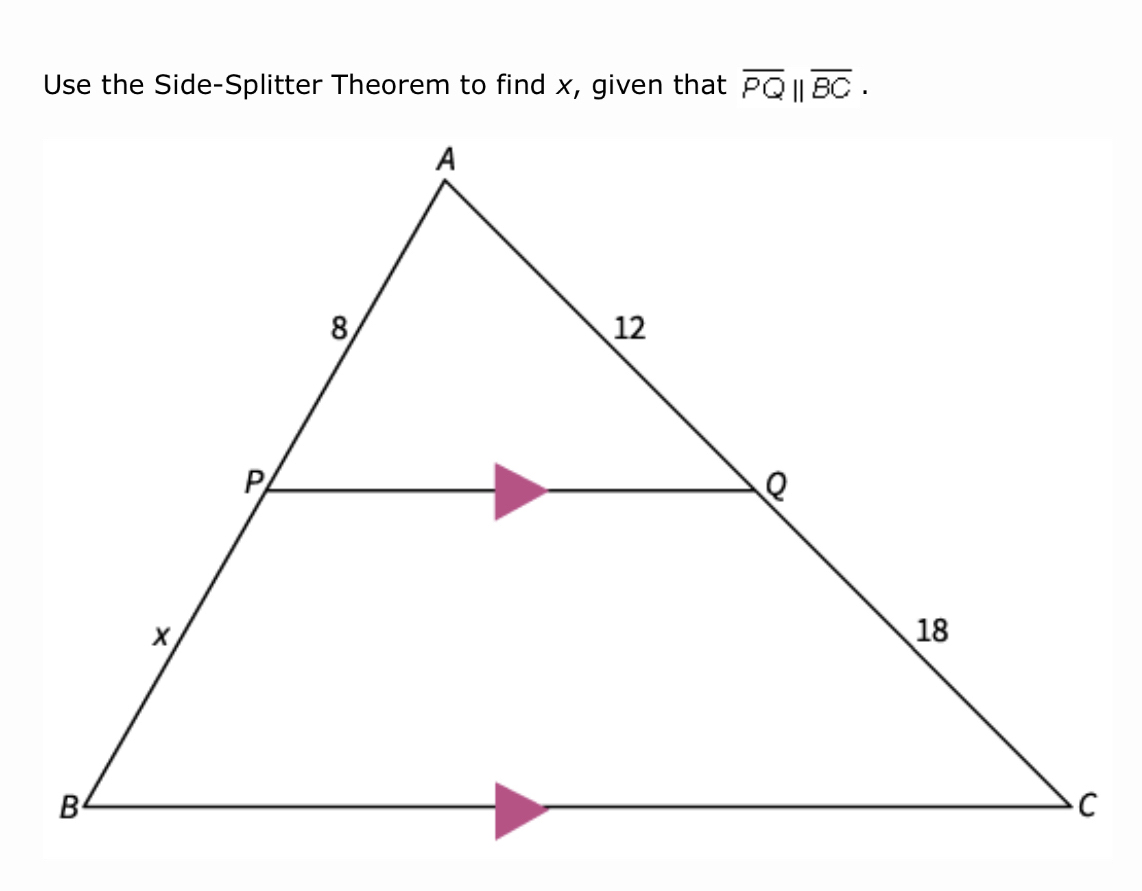
The polygons are similar. Find the value of x.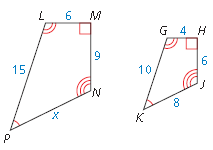
x = 12
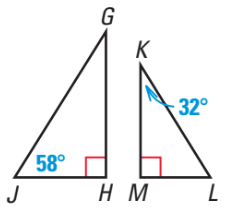
Determine whether the triangles are similar. If they are, write a similarity statement. SHOW WORK.
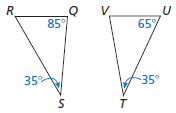
no; m∠R = 60°
Name all the possible quadrilaterals that the statement is true for:
Diagonals are congruent
Rectangle & Square
Determine whether △JKL or △RST is similar to △ABC.
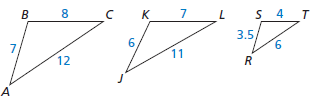
△RST
Which statement is true? A) A trapezoid has 2 pairs of parallel sides. B) A parallelogram has 2 pairs of parallel sides. C) A Square has only 2 right angles. D) A rectangle has only 5 sides.
B) A parallelogram has 2 pairs of parallel sides.
The polygons are similar. Find the value of x.
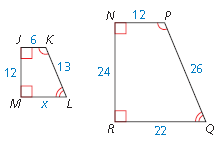
x = 11
Determine whether the triangles are similar. If they are, write a similarity statement. SHOW WORK.
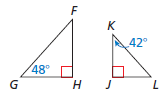
yes; ∠H ≅ ∠J and ∠F ≅ ∠K, so △FGH ∼ △KLJ.
In the diagram VWXY is a parallelogram, complete each statement
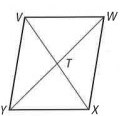
<VYX is supplementary to ? and ?.
<VYX is supplementary to <WVY & <WXY
x = 12
A quadrilateral with 1 pair of parallel sides, 1 pair of equal sides, and no right angles
Isosceles Trapezoid
The polygons are similar. Find the values of x and y.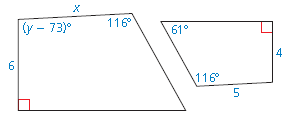
x = 7.5, y = 166
Show that the two triangles are similar.
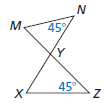
∠N ≅ ∠Z and ∠MYN ≅ ∠XYZ (vertical angles), so △MYN ∼ △XYZ.
Name all the possible quadrilaterals that the statement is true for:
Opposite sides are parallel
Parallelogram, Rhombus, Rectangle, & Square
DE || AC
Find AB
AB= 44.8
This is a correct similarity statement for these two triangles.
What is
△JGH~△LKM?
The polygons are similar. Find the values of x and y.
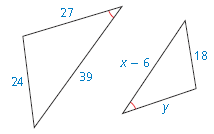
x = 35.25, y = 20.25
Show that the two triangles are similar.
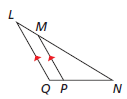
∠Q ≅ ∠MPN (corresponding angles) and ∠N ≅ ∠N, so △LNQ ∼ △MNP.
Prove that the following points represent the vertices of a rectangle:
M: (3, -4) , N: (3, 7) , P: (-5 , -4) , Q: (-5 , 7 )
slope of MN & PQ =undefined
slope of NQ & MP =0
measure of MN & PQ = 11 units
measure of NQ & MP = 8 units
In Exercises 5 and 6, fi nd the value of x that makes △DEF ∼ △XYZ.
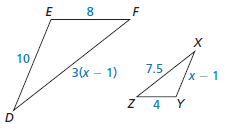
x = 6
A quadrilateral with 2 pairs of parallel sides and 4 equal sides, but no right angles
Rhombus
Autumn is 1.25 meters tall. At 10 a.m., she measures the length of a tree's shadow to be 22.85 meters. She stands 18.3 meters away from the tree, so that the tip of her shadow meets the tip of the tree's shadow. Find the height of the tree to the nearest hundredth of a meter.
The tree is 6.28 m tall.
Sow that the triangles are similar and write a similarity statement. Explain our reasoning.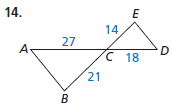
∠ACB ≅ ∠DCE and CE/CB = DC/AC, so △ABC ∼ △DEC.
Prove that the following points represent the vertices of a parallelogram:
A: ( 2 , 4 ) , B: ( 4 , -3 ) , C: ( 9 , -6 ) , D: ( 7 , 1 )
slope of AB & CD = -7/2
slope of BC & AD = -3/5
measure of AB & CD = root 53
measure of BC & AD = root 34
How tall is the person? (feet, inches)

4 feet 4 inches