Oh-my!
Oh-my!
Early Grecian philosophers began to accept that the surface of the Earth is curved while charting star patterns and movements in the sky. They realized that at certain times of the year, some stars were no longer visible to them, but in traveling to other distant places, they could again see particular stars. The curved surface of the Earth compares to which undefined term in Euclidean geometry?
What is plane?
Determine the midpoint of a line segment with endpoints located at (-3, -1) and (7, -5).
What is (2, -3)?
Andrew constructed a proof to verify that vertical angles are congruent. Part of Andrew's proof is shown below.

What is the reason for step 3?
What is substitution?
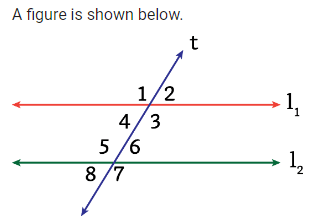
The relationship between angles 7 and 3.
What are corresponding angles?
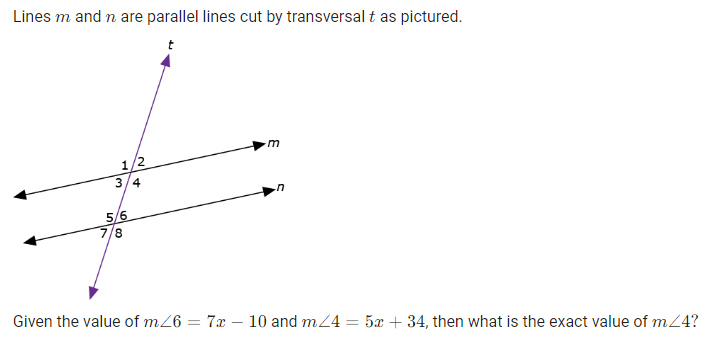
What is 99 degrees?
The parallel postulate of Euclidean geometry is stated below.
Through any point not on a given line, there is exactly one line that passes through the point that is parallel to the given line in the same plane.
Complete the statement describing spherical geometry below.
In spherical geometry, there is ____ parallel postulate because ____.
What are no because parallel lines do not exist?
Line segment AC is twice as long as line segment BC. If AC is represented by 2x+4 and BC is represented by 3x−12, find the value of x .
What is x=7?
Two lines are cut by a transversal. If you want to show that the lines are parallel, which of the following angle pairs would be proof of congruency?
I. Alternate interior
II. Vertical
III. Consecutive interior
IV. Alternate interior
V. Corresponding
What are I, IV, and V only?

The two relationships between angles 4 and 6.
What are congruent angles and alternate interior angles?
Determine the equation of the line that passes through the point (7, 0) and is parallel to the line 8x + 4y = 6.
What is y = -2x + 14?
Which of the following statements is true in both Euclidean geometry and spherical geometry?
F. Vertical angles are congruent.
G. For every line, there is another line parallel to that line.
H. The sum of the measures of the interior angles of a triangle is 180°.
J. Triangles are similar if each has interior angles with measures x° and y°.
What is vertical angles are congruent?
On a map, Devon's house is located at (-3, 5) and Hayley's house is located at (3, -3). What is the distance between Devon's house and Hayley's house?
What is 10 units?
Andrew constructed a proof to verify that vertical angles are congruent. Part of Andrew's proof is shown below.

What is the missing statement & reason for step 9?
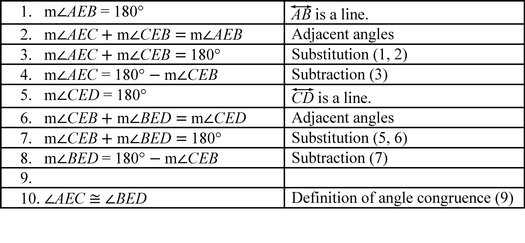
What is m∠AEC = m∠BED by the Transitive Property?
Given the map below, which two streets must be parallel? (not drawn to scale)
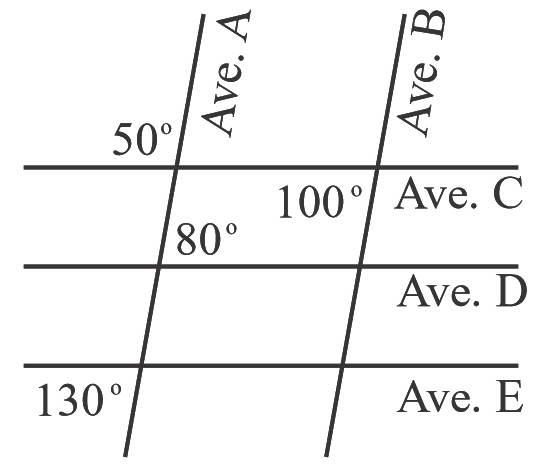
What are Ave. C and Ave. E?
and
intersect at point Z, creating angles 1, 2, 3, and 4. m∠1 = 4x + 8 and m∠2 = 7x + 7. Determine the value of x.
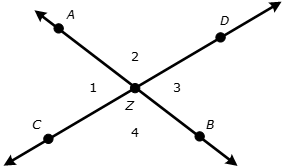
What is x=15?
Two angles in a triangle are shown on the surface of a sphere.
What value is NOT a possible angle measure for ∠C?
F. 115°
G. 90°
H. 35°
J. 40°
What is 35 degrees?
In the diagram:
m||n, r||s, angle1congangle11, angle4congangle10, angle2congangle8, angle9congangle15, and angle8congangle14.
The conjecture that can be made about the geometric relationship shown in the pattern between parallel lines and angles?
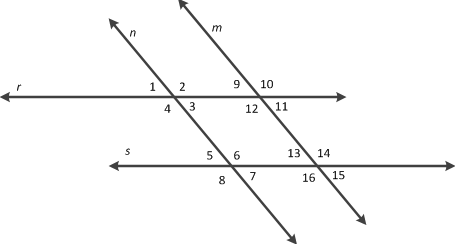
What is if two lines are parallel and cut by a transversal, then alternate exterior angles are congruent?
A conditional statement is shown.
If a triangle has an interior angle that measures 60°, then the triangle is an equilateral triangle.
The given conditional statement is ____, and the converse of the statement is ____.
What are false, then true?
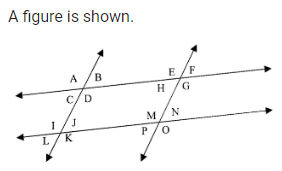
The only angles to make a linear pair with angleM .
What are
angleN and angleP?
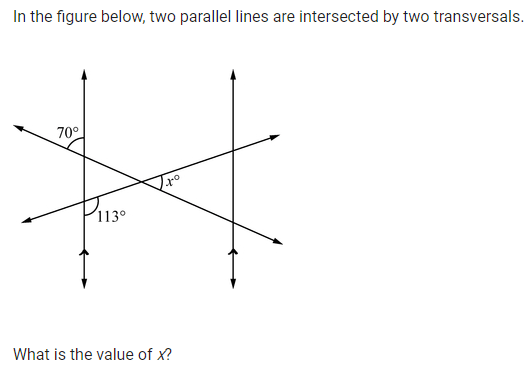
What is 43 degrees?
Which table below correctly compares geometric relationships in Euclidean and spherical geometries?
A.
B.
C.
D.
What is choice D?
In the figure below, k ∥ t and k ⊥ q .
Based on this information, this statement can be proven true.
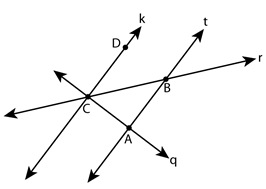
A.∠ ACB ≅ ∠ ABC
B.Δ CAB is an acute triangle.
C.Δ DCB ≅ ∠ BCA
D.Δ CAB is a right triangle.
What is Δ CAB is a right triangle?
A true conditional statement is shown.
If the diagonals of a rectangle are perpendicular, then the rectangle is a square.
Which row in the table identifies the converse, inverse, and contrapositive statements of the given conditional statement?
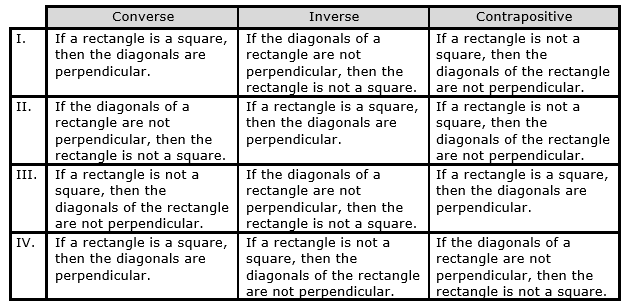
What is Row 1?
A figure is shown below. This is an angle vertical to
angleEBC.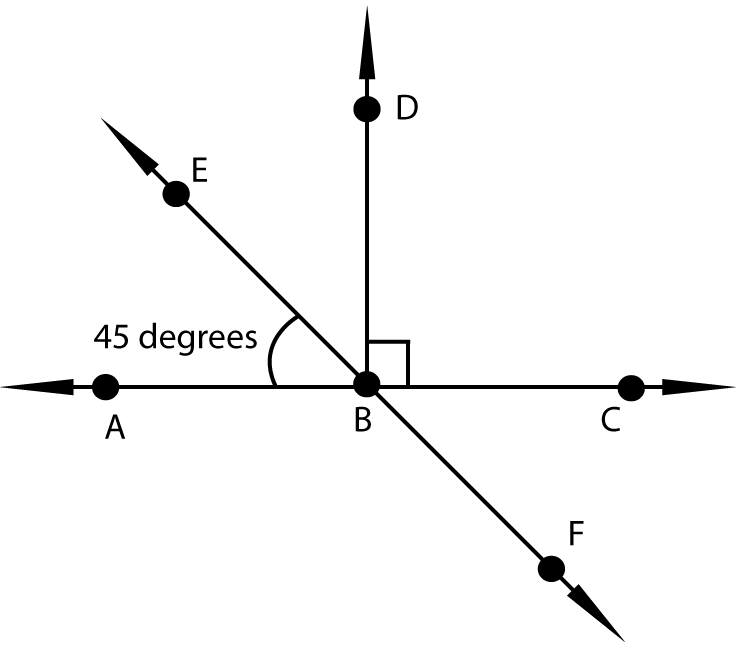
What is
angleABF?
Segment AB has endpoints at (-2,3) and (10,7). What is the equation of the perpendicular bisector (midpoint) of that segment?
What is y = -3x + 17 ?