Inscribed and Central Angles
Cylinder, Sphere and Cone Volume
Arc Length and Area of the Sector
Sum of Interior/ Exterior Angles of Polygons
Right Triangles
100
Solve for x
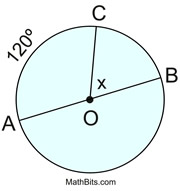
AB is a diameter
AC is 120, Semicircle ACB is 180
CB is 60: 180-120
100
What is the volume? Round to the nearest whole number.
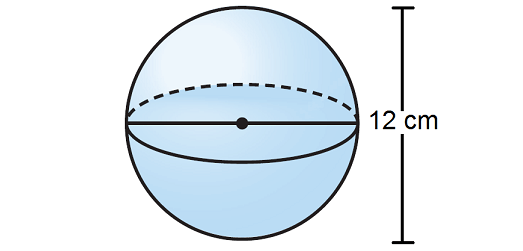
Sphere V = 4/3pir^3
Sphere V = 4/3pi(6)^3
Sphere V = 905 cm^3
100
Find the Arc Length. Round to the nearest foot.
l = 2pir *x/360
l = 2pi(16.50) * 39/360
11 ft
100
What is the sum of Interior Angles of a decagon?
s = (n-2) *180
s = (10-2) * 180
s = 8 *180
s = 1440
100
482 + 142 = c2
2500 = c2
50 = c
200
Angle ACB is 47 degrees (Inscribed Angle)
Intercepted AB arc is 94 degrees (47 x 2)
Angle AOB is 94 degrees (Central Angle)
200
What is the volume? Round to the nearest inch.
V = pir^2h
V = pi(7)^2(13)
V = 2,001 inches^3
200
Solve for the Area of a Sector. Round to the nearest tenth place.
SA = pir^2 * x/360
SA = pi(6.5)^2 * 115/360
SA = 42.4 inches^2
200
What is the sum of exterior angles of a pentagon?
360 degrees
200
Round to the nearest tenth place.
sin-1(x) = 11/25
x = 26.1 degrees
300
Solve for angle B
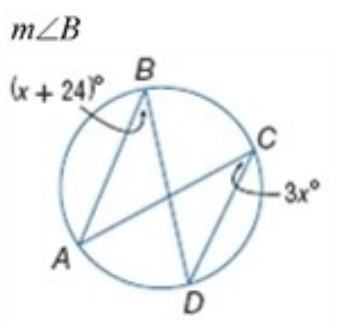
ABD and ACD are inscribed angles with the same intercepted arc AD
ABD = ACD
x+24 = 3x
24 = 2x
12 = x
Angle B = x + 24 -> 12 + 24
Angle B = 36 degrees
300
What is the volume? Round to the nearest hundredth place.
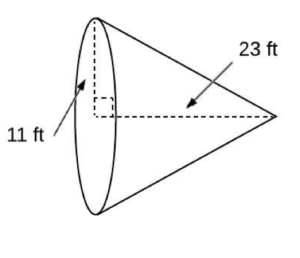
V = 1/3pir^2h
V = 1/3pi(11)^2(23)
V = 2,914.35 ft^3
300
Solve for the Area of a Sector. Round to the nearest thousandth place.
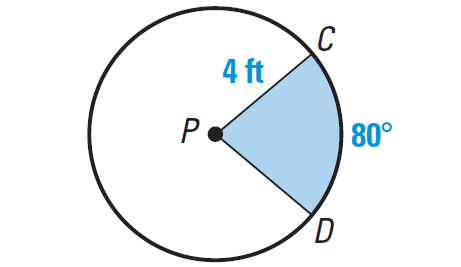
SA = pir^2 * x/360
SA = pi(4)^2 * 80/360
SA = 11.170 ft^2
300
The sum of the interior angles of a polygon is 3960 degrees, How many sides does the polygon have?
Sum of interior angles = (n - 2) x 180
3960 = (n - 2) x 180
3960/180 = (n - 2) x 180/180
22 = n - 2
22 + 2 = n - 2+2
24 = n
300
Round to the nearest hundredth place.
sin(23)=2500/x
x *sin(23) = 2500
x = 2500/sin(23)
x = 6398.26 m
400
Solve for x
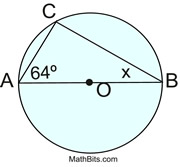
Inscribe Angle CAB is 64 degrees. Its Intercepted Arc CB is 128 = 64 x 2
ACB is a semicircle, which is 180 degrees
Intercepted Arc AC is 52 degrees. The Inscribe angle of CBA is half.
CBA = x = 26 degrees.
400
What is the volume? Round to the nearest hundredth place.
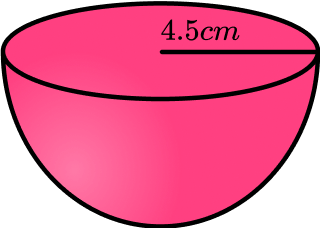
Hemisphere V = 2/3pir^3
Hemisphere V = 2/3pi(4.5)^3
Hemisphere V = 190.85 cm^3
400
Solve for the Area of a Sector of the Major Arc LMK. Round to the nearest cm.
SA = pir^2 * x/360
SA = pi(6)^2 * 240/360
SA = 74 cm^2
400
To manufacture stop signs, the engineers need to determine the measure of each interior angle of the sign. What is the measure of each interior angle if the sign is a regular octagon?
s = ((n-2) *180)/n
s = ((8-2)*180)/8
s = 135 degrees
400
1 mile = 5280 ft
tan(11.87) = x/ 2640
(2640) x tan(11.87) = x
x = 555 ft
500
Solve for measure angle H?
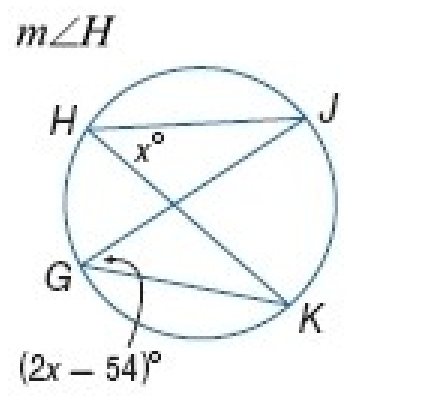
The inscribed angles of Angle JHK = JGK for the same intercepted arc JK
JHK = JGK
x = 2x - 54
-x = -54
x = 54
Angle H = 54 degrees
500
What is the volume of the entire figure? Leave in terms of pi
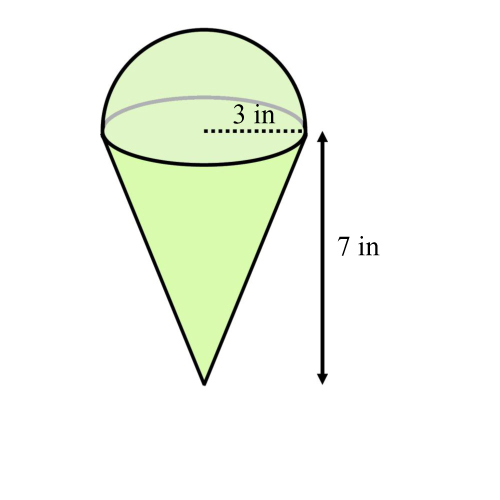
Hemisphere V = 2/3pir^3
Hemisphere V = 2/3pi(3)^3
Hemisphere V = 18pi inches^3
Cone =
1/3pir^2h
1/3pi(3)^2(7)
Cone V = 21pi inches^3
Total Volume = 18pi +21pi = 39pi inches^3
500
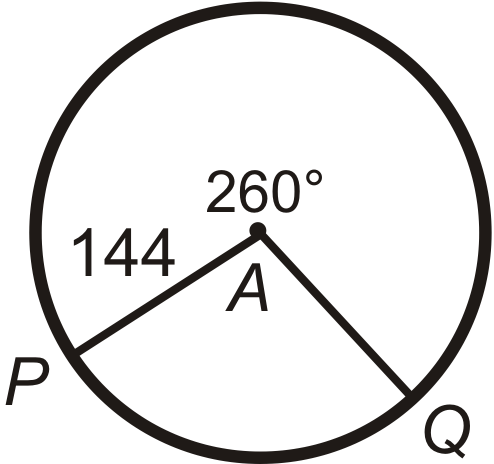
Solve the Arc Length for the minor arc PQ. Round to the nearest hundredth place.
l = 2pir *x/360
l = 2pi(144) * 100/360
l = 251.33 units
500
What is the measure of each exterior angle of a 20-gon?
Each Exterior Angle = 360/n
Each Exterior Angle = 360/20
Each Exterior Angle = 18 degrees
500
Steve is turning half of his backyard into a chicken pen. His backyard is a 24 meter by 45 meter rectangle. He wants to put a chicken wire fence that stretches diagonally from one corner to the opposite corner.
How many meters of fencing will Steve need?
a^2 + b^2 = c^2
24^2 + 45^2 = c^2
576 + 2025 = c^2
2601 = c^2
51 m = c