Sine, Cosine and Tangent
Similar ∆
Congruent ∆
Pythagorean Theorem and Special Right ∆
Circles
100
What is the phrase we use to help us remember our Trigonometric Ratios?
SohCahToa
100
What are two of the three similarity Theorems
AA Theorem, SSS Theorem, SAS Theorem
100
Are these triangles congruent? If yes, by what theorem?
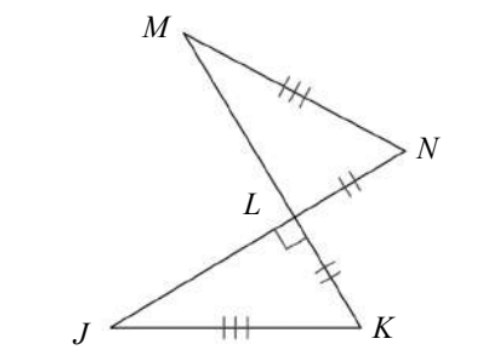
Yes! By HL
100
Find the perimeter:
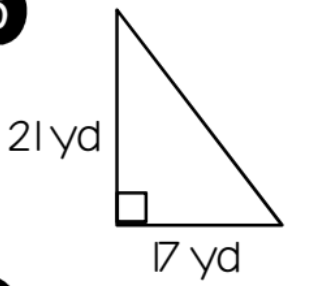
65 yards
100
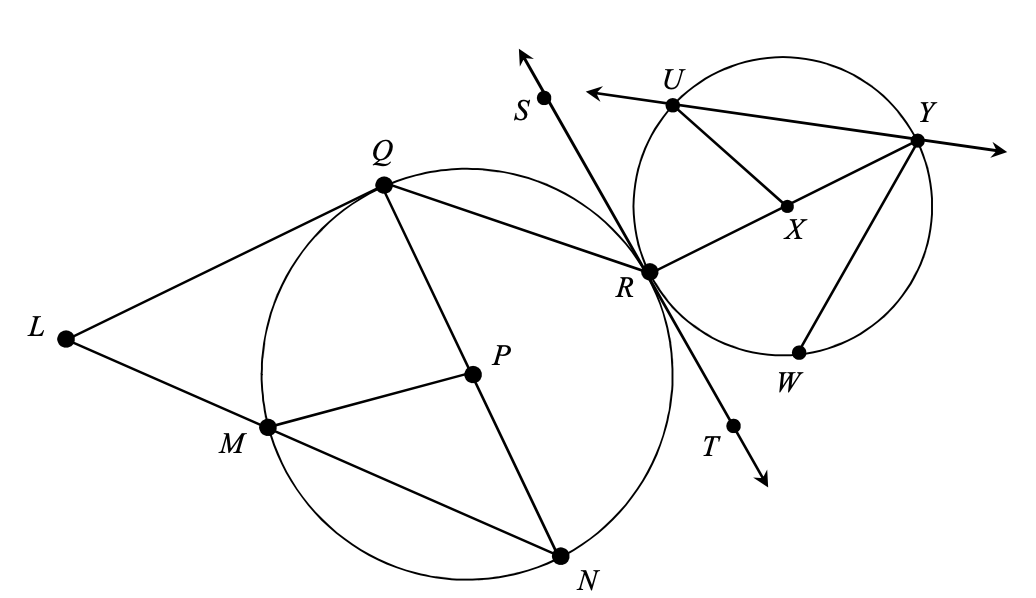
Name 2 inscribed angles
Answers Vary!
200
What ratio is equal to
(opp)/(adj)
Tangent (or Tan)
200
Corresponding angles in similar triangles are _______.
Congruent
200
What theorem would you use to prove:
SAS
200
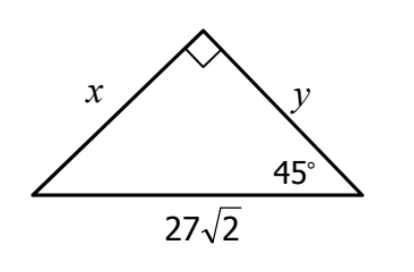
Find the missing side. Leave your answer in simplest radical form:
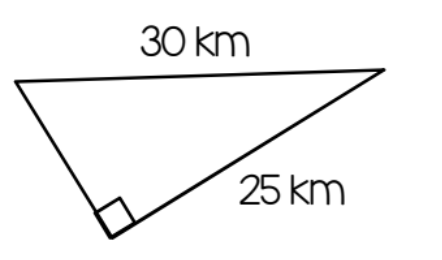
5sqrt(11)
200
Find the area and circumference using proper units of measure rounded to the nearest tenth:
C = 32.0 m
A = 81.7 m2
300
Find x to the nearest ten-thousandth ;)
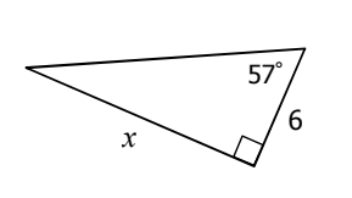
9.2392
300
Are these two triangles similar? How do you know?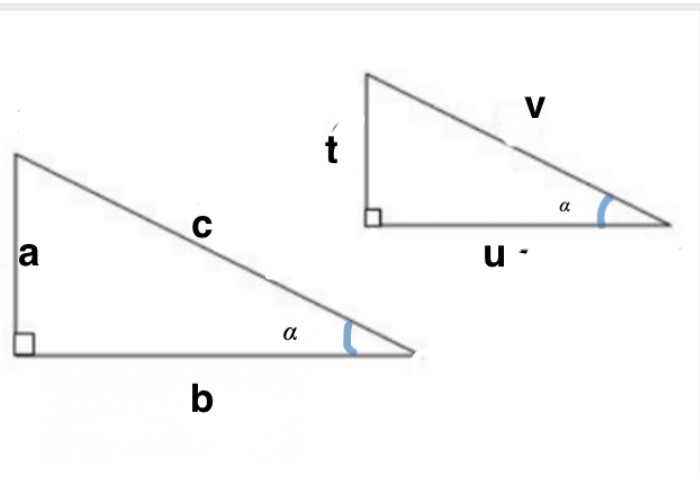
yes, AA Theorem.
300
What theorem proves these congruent?
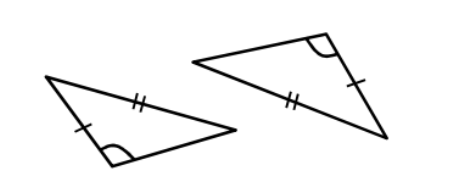
Not Possible!!!!
300
Find x and y:
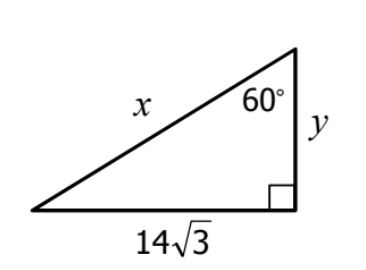
x = 28
y = 24
300
Arc UT is 112o, find the measure of arc US.
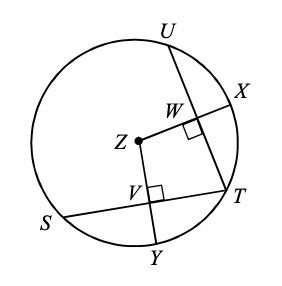
136o
400
Find x. Round to the nearest hundredth
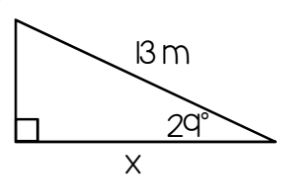
11.37
400
Are these two triangles similar? How do you know?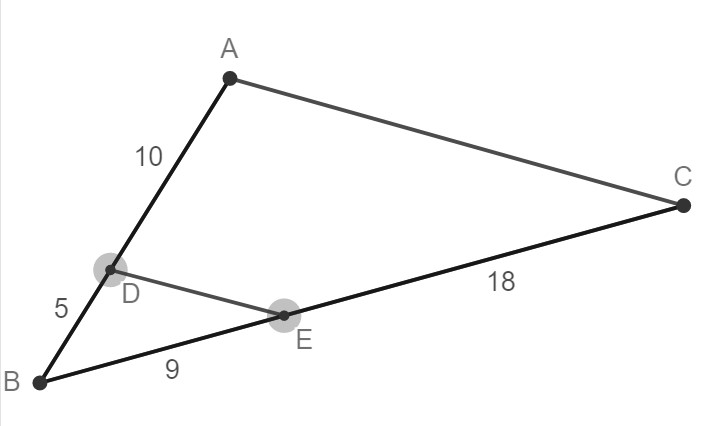
yes, SAS theorem.
400
What steps are needed to prove:
400
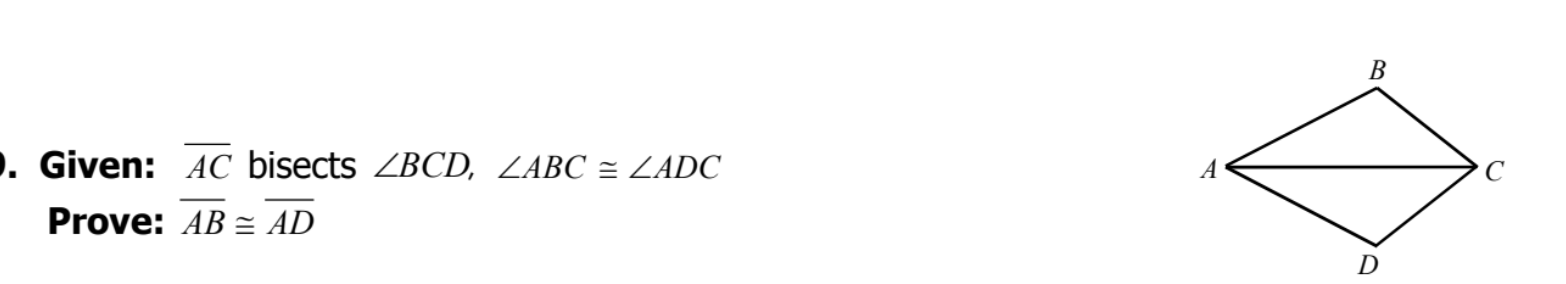
Find the perimeter in radical form:
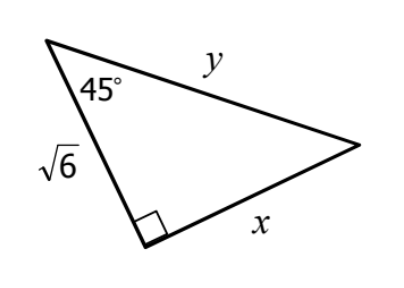
2sqrt(6) + sqrt(12)
or
2sqrt(6) + 2sqrt(3)
400
Angle JKL is (3x + 6)o. Find x.
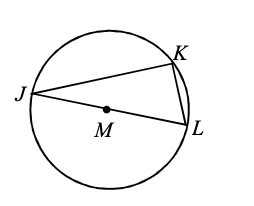
x = 28
500
What is the measure of Angle A to the nearest tenth?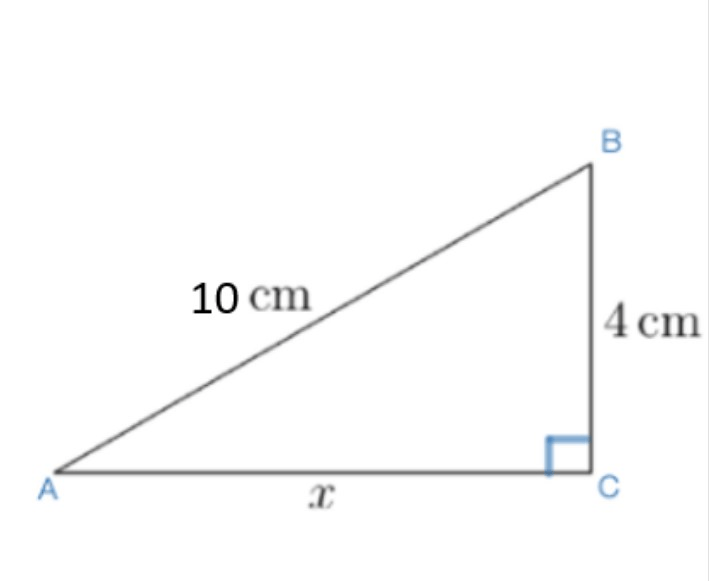
23.6o
500
∆BYK ~ ∆ZYT. Find YK.
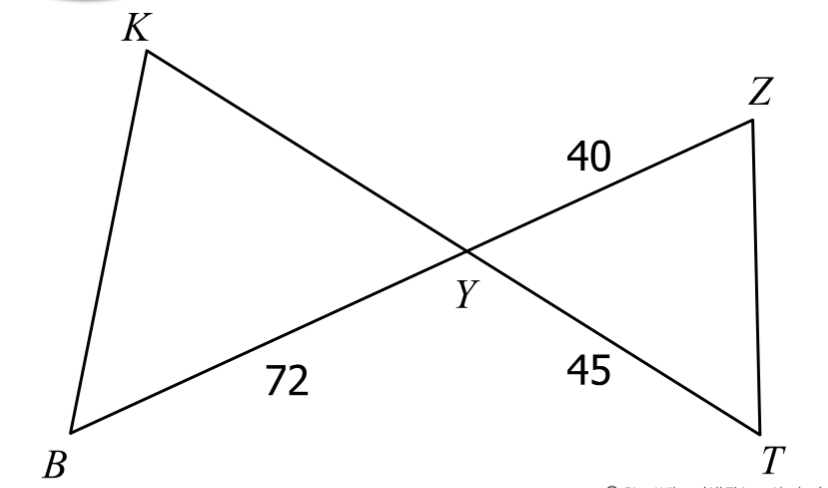
81
500
What are the steps to prove:
500
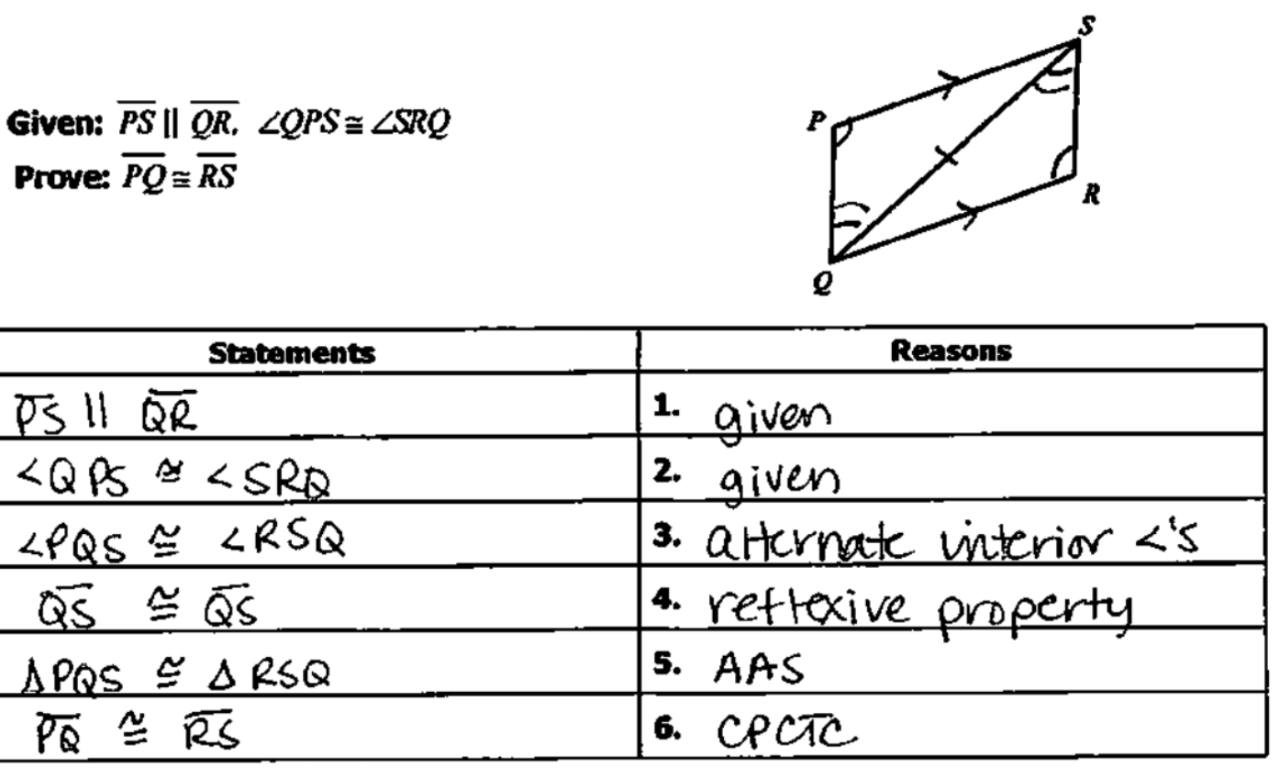
Find the area:
364.5 units2
500
What is the equation of this circle?
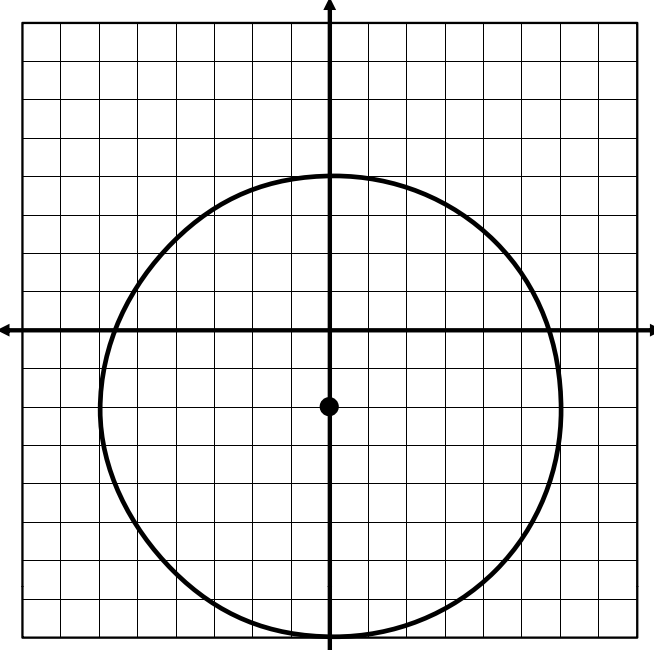
x2 + (y + 2)2 = 36