Parallel, Perpendicular or Neither
Vertical Angles + Angle Bisectors
Supplementary Showdown
Congruence Connections
Midpoint + Addition Postulates
Parallel Lines Cut by a Transversal
100
Lines with the same slope are always this.
Parallel.
100
What kind of angles are 1 and 4, 2 and 3, 5 and 8, and 6 and 7, respectively?
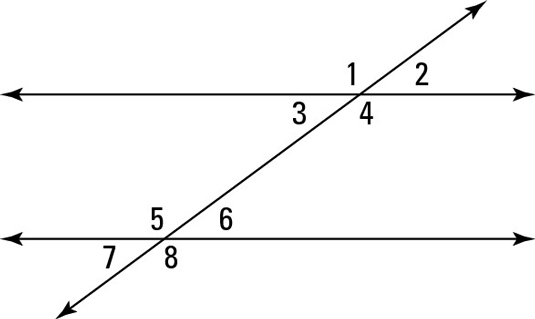
Vertical angles.
100
“Supplementary” means the two angles add to…
180 degrees.
100
If △ABC≅△DEF, then ∠B corresponds to…
∠E.
100
What is the midpoint formula for endpoints (x1,y1), (x2,y2).
((x1+x2)/2, (y1+y2)/2)
100
If two parallel lines are cut by a transversal, corresponding angles are always…
Congruent.
200
Lines with opposite reciprocal slopes are always this.
Perpendicular.
200
An angle bisector splits an angle into two angles that are...
Congruent.
200
∠A and ∠B are supplementary. If m∠A=115 degrees, find ∠B.
m∠B=65 degrees.
200
If quadrilateral BCDE is congruent to OPQR, then ∠C is congruent to which angle?
∠P.
200
Find the midpoint of (−4,6) and (8,−2).
(2,2).
200
Assume the two horizontal lines are parallel. If m∠2=50 degrees, what is m∠6?
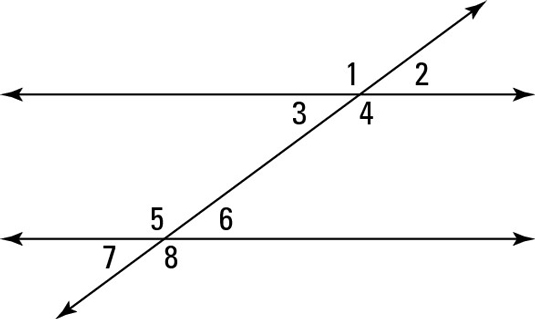
m∠6=50 degrees. (Corresponding angles are congruent.)
300
Classify:
y=3x−2
and
y=3x+10
Parallel.
300
If one angle is 72 degrees, what is its vertical angle?
72 degrees.
300
∠A and ∠B are supplementary angles, where ∠A=1+2x and ∠B=x-49. Find x.
x=76.
300
If quadrilateral BCDE is congruent to OPQR, then QR is congruent to which segment?
DE.
300
In the figure above AB=5x + 8 and BC=3x + 10. If AC=98 find the length of segment AB.
AB=58.
300
Assume the two horizontal lines are parallel. If m∠2=50 degrees, what is m∠3?
m∠3=50 degrees. (Vertical angles are congruent.)
400
Classify:
y=4x+1
and
y=-1/4x+7
Perpendicular.
400
AB is an angle bisector of ∠CAD. Find x.
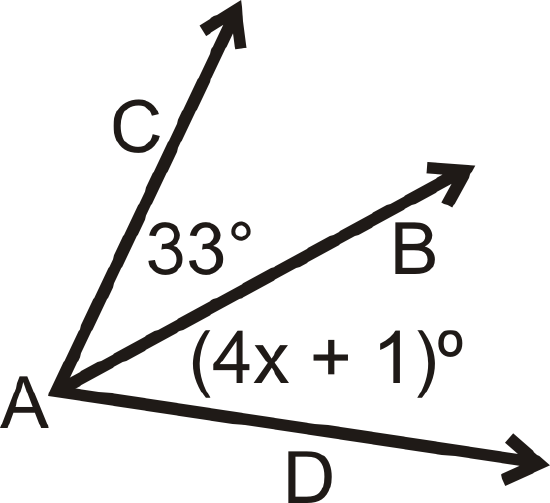
x=8.
400
∠A and ∠B are supplementary angles, where ∠A=16x-2 and ∠B=20x+2. Find m∠A.
m∠A=78 degrees.
400
If quadrilateral BCDE is congruent to OPQR, then BE is congruent to which segment?
OR.
400
In the figure above AB=6x + 4 and BC=5x + 12. If AC=126 find the length of segment AB.
AB=64
400
Assume the two horizontal lines are parallel. If m∠2=50 degrees, what is m∠5?
m∠5=130 degrees. (Same-side interior angles are supplementary.)
500
Line 1 goes through (−2,5) and (4,−1). Line 2 is
y=x+3
Classify.
Perpendicular. (Line 1 slope −1, line 2 slope 1.)
500
DB is an angle bisector of ∠ABC. Find m∠DBC.
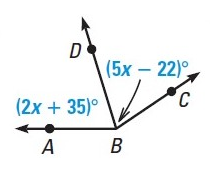
m∠DBC=73 degrees.
500
Find the value of x.
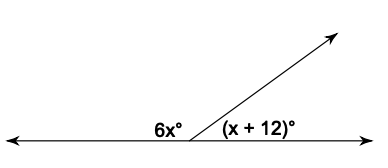
x=24.
500
Write a statement that indicates that the triangles are congruent.
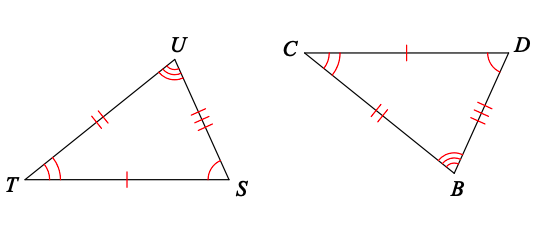
△STU≅△DCB.
500
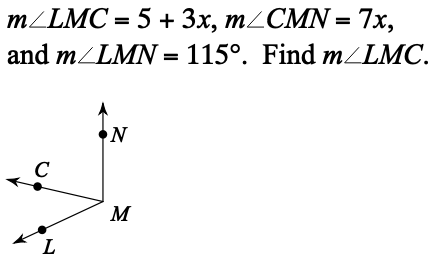
m∠LMC=38 degrees.
500
Same-side interior angles are supplementary. If they’re 4x+20 and 2x+40, find x.
x=20.