Geometry Proof Basics
Triangle Properties
SSS, SAS, ASA, HL & AAS Theorems
Name that Reason
Miscellaneous
100
What are the headings of the 2 columns in a proof?
Statements and Reasons
100
How do we know that <AEC=<DEB below?
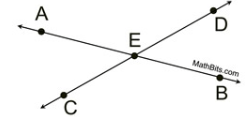
Vertical Angles
100
If none of the angles are marked congruent between 2 triangles, what is the only theorem you can use?
SSS
100
What is the "Reason" for Statement #1 below?
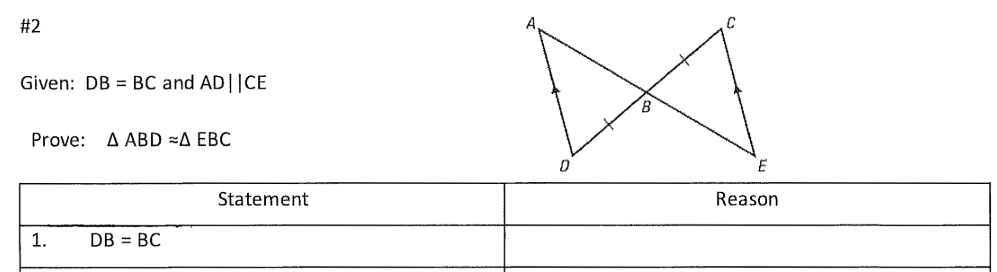
Given
100
What does the "L" stand for in the HL congruence theorem?
Leg
200
Information given to you, either written or in a diagram, what should you write as the reason?
Givens
200
How do we know that CA=CA below?
Reflexive Property
200
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then these two triangles are congruent how?
SAS
200
Double points for luck!!
Double Points
200
Name all 5 triangle congruence theorems.
SSS, SAS, AAS, ASA and HL
300
What do we call a statement that looks like below?
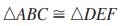
Congruence Statement
300
Name the 4 angles that point "E" the vertex of?
<AEC (or <CEA)
<DEB (or <BED)
<AED (or <DEA)
<CEB (or <BEC)
NOTE:
300
If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then these two triangles are congruent how?
ASA
300
What is the reason for statement #3 below?
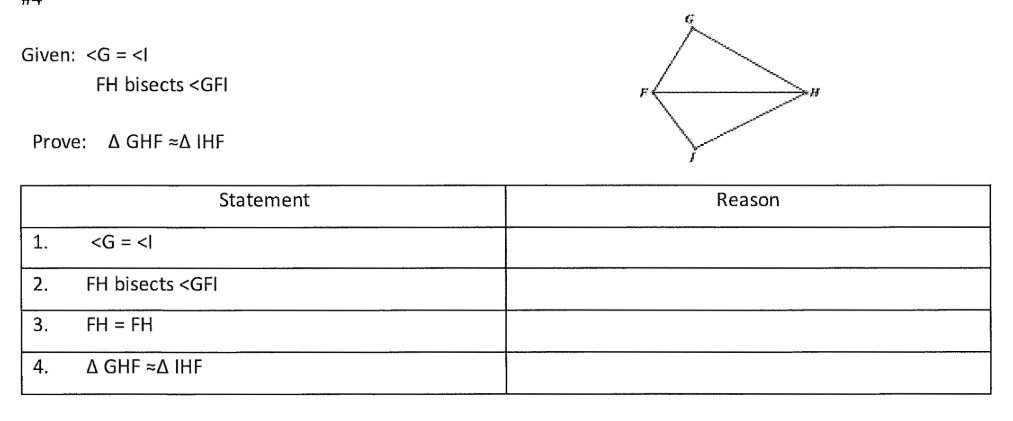
Reflexive Property
300
Given the congruence statement below, what side is congruent to side CB?
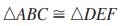
FE
400
What do we call the side across from the right angle in a right triangle?
Hypotenuse
400
In the triangle below, if "D" is the midpoint of AC, what is AD congruent to?
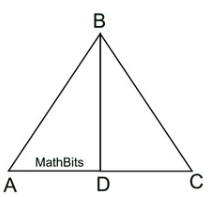
DC
400
If two angles and the non-included side one triangle are congruent to two angles and the non-included angle of another triangle, then these two triangles are congruent how?
AAS
400
What is the reason for statement #3 below?
Vertical Angles
400
What congruence theorem can be used to prove the triangles below are congruent?
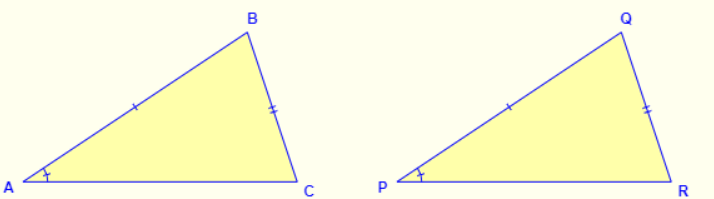
Not congruent, SSA is not a congruence theorem.
500
Other than "given", name 3 other things you can list as a reason in a geometry proof?
Answers vary.
Midpoint, bisector, alternate interior angles, reflexive property, vertical angles or AAS/SSS/SAS/ASA/HL
500
IF DB bisects <B, what angle is <DBC congruent to?
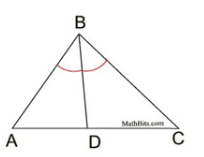
<DBA or <ABD
500
What theorems can you use to prove right triangles are congruent?
SSS, SAS, AAS, ASA, HL
(All of them)
500
In the triangles below, AD || CE. Name 2 angles that must be congruent.
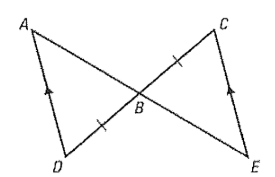
<A and <E OR <D and <C
500
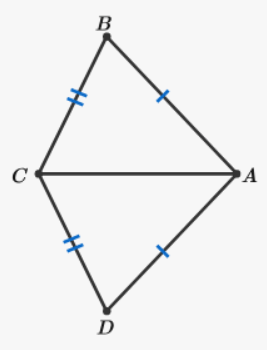
Name TWO congruence theorems that can be used to prove the triangles below are congruent.
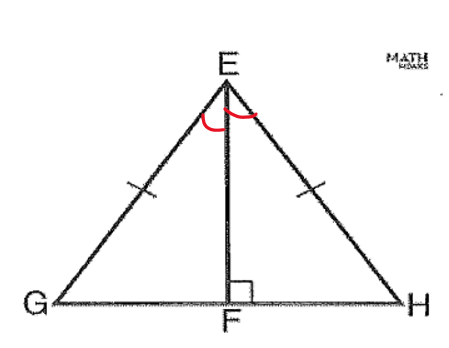
HL, SAS or AAS