Isosceles & Equilateral Triangles
Pythagorean Theorem
SSS, SAS, ASA, AAS & HL Theorems
CPCTC
100
What is the value of x?
x = 60 degrees
100
In a2 + b2 = c2, which side must always be substituted in for c?
The hypotenuse (the longest side)
100
What must be true for the triangle to be congruent by HL?
100
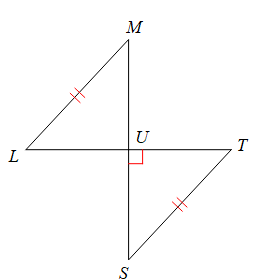
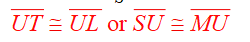
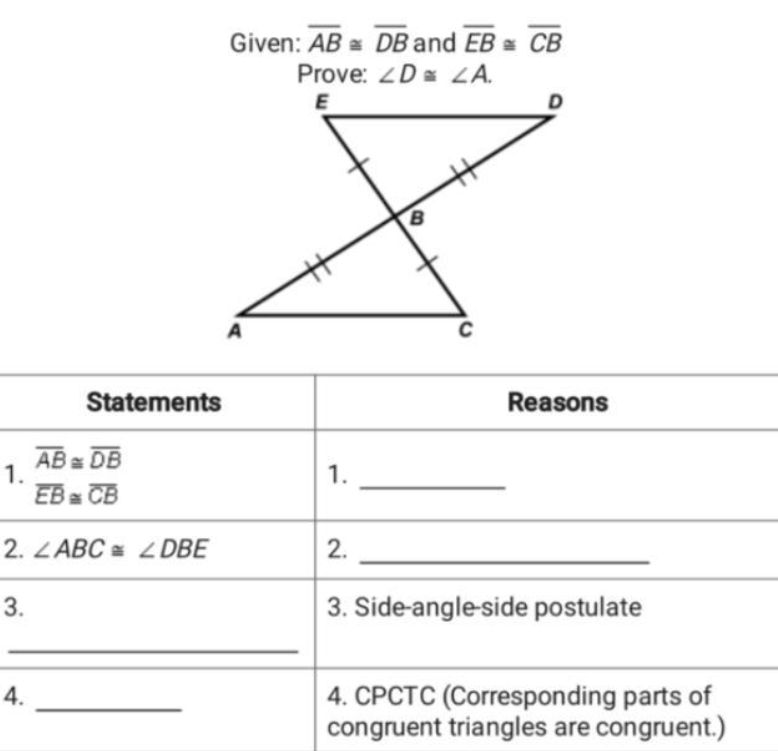
What's the reason for #2?
Vertical angles
200
What is the value of x?
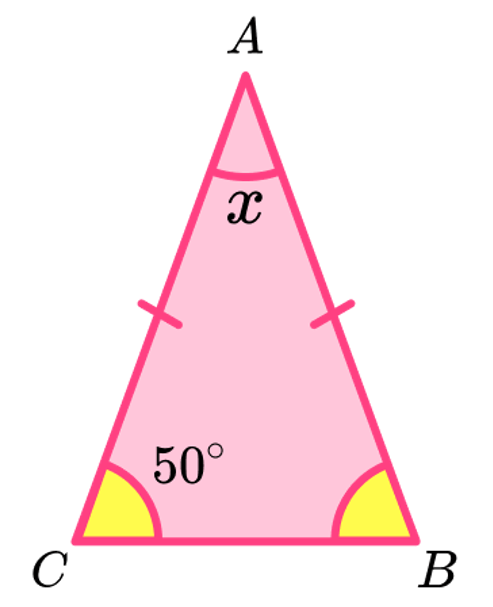
x = 80 degrees
200
Find the length of the BC
BC = 20
200
Are these triangles congruent? If so, which postulate or theorem proves it?
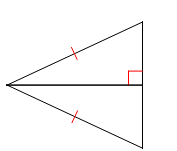
Yes, HL
200
What is the missing reason in #3?
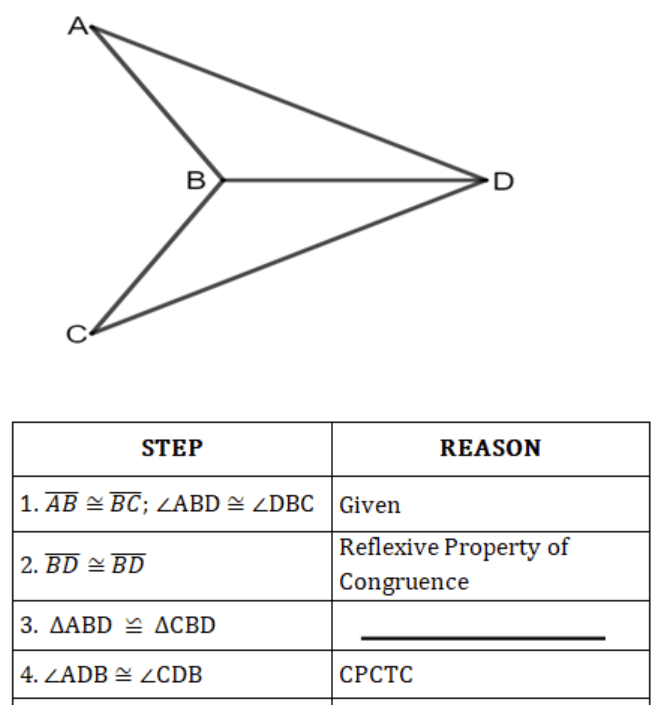
SAS
300
Find the length of each side of this equilateral triangle:
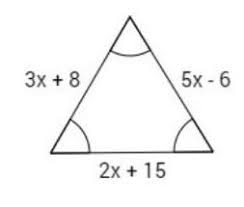
29
300
Find the length of the hypotenuse. Write your answer in simplest form.
square root 130
300
Are these triangles congruent? If so, which postulate or theorem proves it?
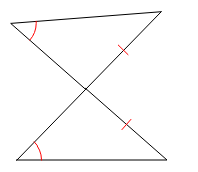
Yes, AAS
300
How are the overlapping triangles triangle DEF and triangle GFE congruent?
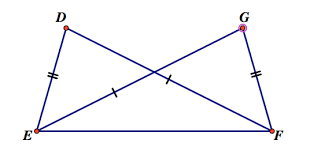
SSS
400
Find the length of the base.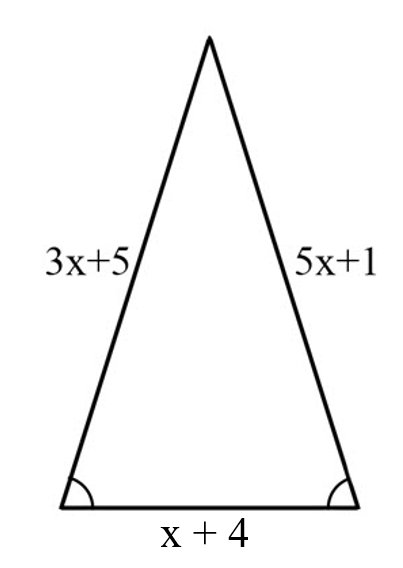
6 units
400
If three sides of a triangle are 40, 9, and 41, is it a right triangle?
Yes, 1681 = 1681
400
What must be true for the two triangles to be congruent by ASA?
400
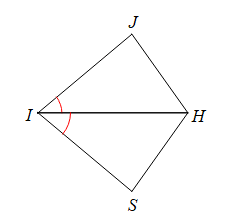
What is the reason for #4?
CPCTC
500
1) What is the value of x?
2) What is the measure of angle B?
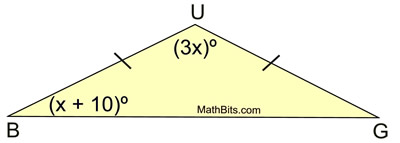
1) x = 32
2) The measure of angle B is 42 degrees.
500
Find the length of the missing leg of the right triangle. Write your answer in simplest radical form.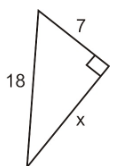
5* square root 11
500
Name THREE congruence theorems that can be used to prove the triangles below are congruent.
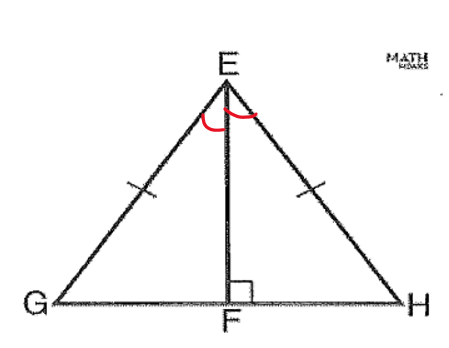
What are SAS, AAS, HL
500
1) Which postulate or theorem proves that the overlapping triangles are congruent?
2) How is angle A cong to angle A?
1. ASA 2. Reflexive Property