Name the following rigid motions:
1. A turn
2. A flip
3. A slide
1. Rotation
2. Reflection
3. Translation
A motion that increases or decreases size is a ______________.
dilation
With what transformation does the orientation change?
A reflection
What is the minimum degree of rotation that will map the figure onto itself?
120 degrees
Determine the rigid motion in the image below:
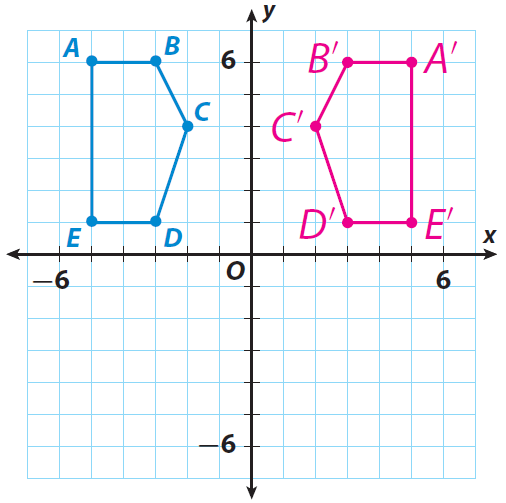
A reflection
Determine the y-coordinate of C' after a dilation with a scale factor of 1.5 centered at the origin.
3
This transformation preserves angle measurements but not segment lengths.
dilation
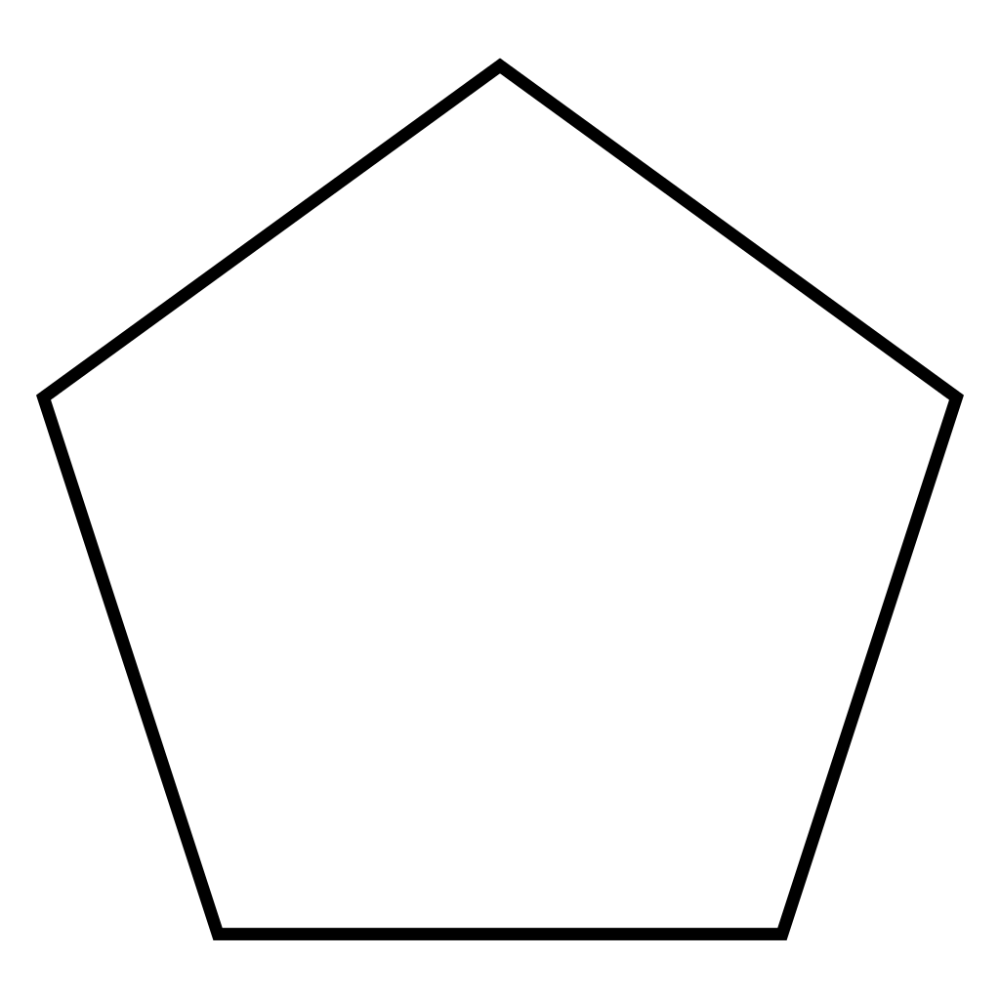
What type or types of symmetry does the figure below have? Rotational, Reflectional, Both or Neither

Both rotational and reflectional
What line or lines of reflection does the figure have? Vertical, Horizontal or both?
Vertical
After a dilation with a scale factor of 2, T'A' = ___ TA. (what numerical value)
2
Select the word that makes the statement true.
After a sequence of transformations including a dilation with a scale factor of 1/4 and a reflection over the line x=2, the angle measures are (preserved or not preserved), but the image is a (enlargement or reduction).
preserved & reduction
Describe the transformation or transformations that will take angle FHB to angle DGH
A translation and a reflection
According to the algebraic rule (x,y) -> (x-2, y+3), in what direction and distance will the pre-image transform?
left 2 and up 3
After a dilation with a scale factor of 2 centered at (0,0), this segment will overlap TH.
segment T'H'
Describe the transformations that occur with the following function notation:
-f(x-3)
A reflection across the x-axis and a translation right 3 units
Use function Notation to describe the transformation from angle EHB to angle HGD.
y = f(x-3)+3
Point A is located at (3,2). Determine the coordinates of A' after a 270 degree counterclockwise rotation.
(2,-3)
After a dilation with a scale factor of 2 centered at (0,0), the slope of this segment will be equal to the slope of HM.
The vertices of a triangle are J(3,0), H(0,3), and S(-3,0). Which statements are true of the image of JHS after the sequence of transformations:
y= -f(x)
(x,y) -> (2x,2y)
1. H' (-3,0)
2. JHS ≅ J'H'S'
3. J'' (6,0)
4. J'H'S' ~ J''H''S''
5. y=x is a line of symmetry for JHS and J''H''S''
2,3,&4
A sequence of transformations was performed. After a 90 degree counterclockwise rotation, A'(-7,2). What is the algebraic description of the translation that takes A'->A''
(x,y)->(x+2, y-1)