Parallel & Perpendicular Lines
Quadrilaterals
Coordinate Proofs
Congruent Angles
Angles & Polygons
100
What makes the equation of a line parallel? Perpendicular?
Parallel: Same slope
Perpendicular: Opposite Sign Reciprocal Slope
100
A square is ______________ a rectangle.
ALWAYS
100
How do we prove a parallelogram is a square?
A square is a parallelogram that has:
1. 4 right angles
2. Congruent diagonals that are perpendicular
3. Have 4 equal sides
4. Have 2 sets of opposite sides that are parallel.
100
What is the value of x + y?
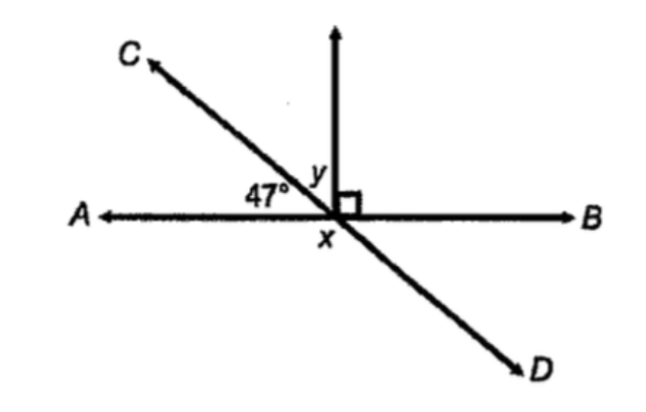
x = 133 degrees
y = 43 degrees
133 + 43 = 176 degrees.
100
What are angles A, B, C and B + D?
A = 120 degrees
B = 60 degrees
C = 120 degrees
B + D = 120 degrees
200
What is the slope of the line f' which is parallel to line f?
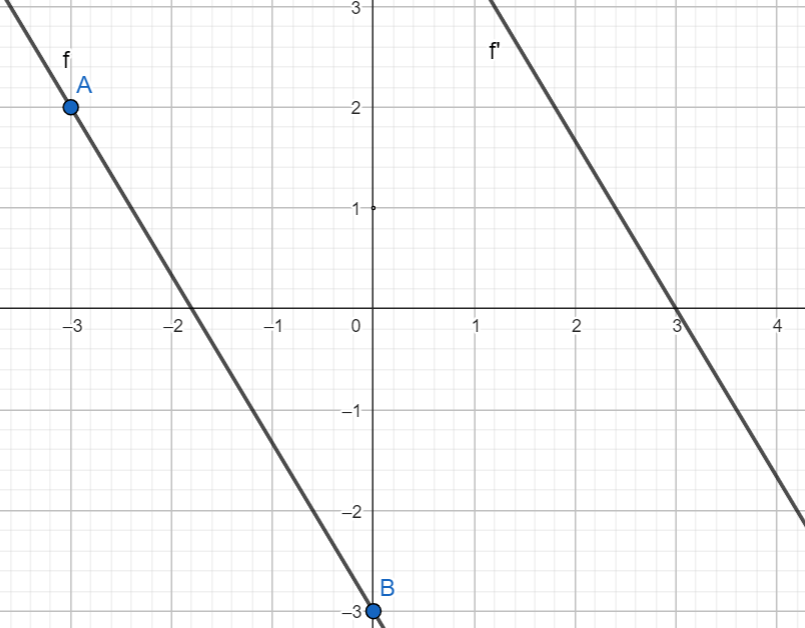
-5/3
200
Each side of a square is 10 cm. How long are the diagonals? (Round to the nearest hundredth)
Diagonals = 14.14 cm
200
The vertices of quadrilateral ABCD are A(-6, 2), B(0, 4), C(-4, 0), D(2, 2). What kind of quadrilateral is ABCD?
A. Trapezoid
B. Square
C. Parallelogram that is not a rhombus
D. Rhombus that is not a square
C. Parallelogram that is not a rhombus
200
The parallel lines are cut by a transversal creating the angles shown. Determine which angles must be congruent to angle x.
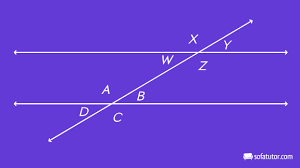
X = Z = A = C
200
What is the value of angle C?
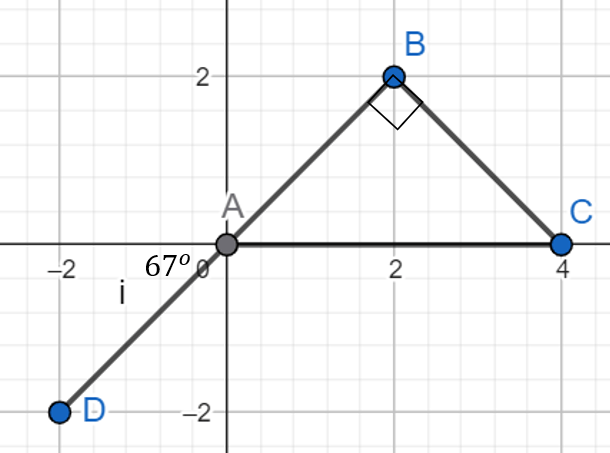
C = 23 degrees
300
What is the slope of the line perpendicular to line AB?
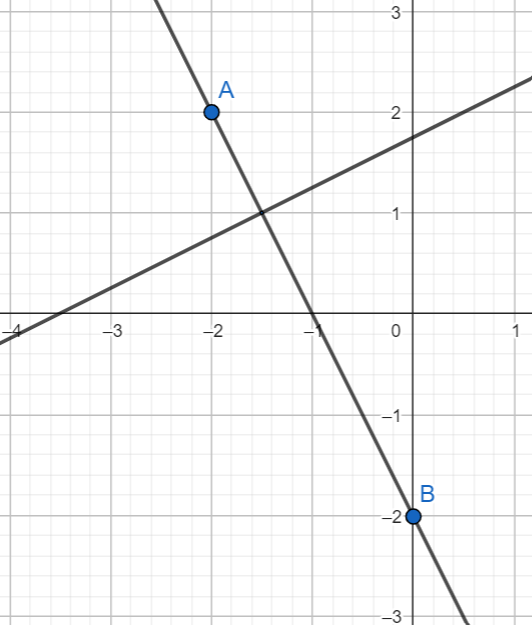
1/2
300
ABCD is a trapezoid. Base AB is 4 cm and base DC is 20 cm. What is the midsegment FE?
FE = 12 cm
300
The ordered pairs that describe the locations of three vertices of a parallelogram on a coordinate plane are given.
(0, 3), (2, 2), (4, 3)
Which ordered pair describes a possible location of the fourth vertex of the parallelogram?
A. (-1, 2) B. (3, -2) C. (1, 5) D. (2, 4)
D. (2, 4)
300
In the figure below, the lines are parallel. What is the value of x?
A. 113 B. 51 C. 141 D. 39
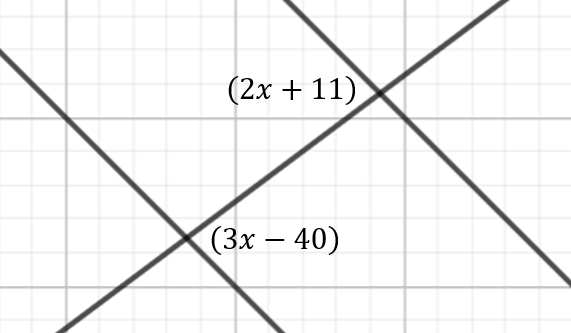
B. 51
300
Find the missing interior angles. (Not to scale)
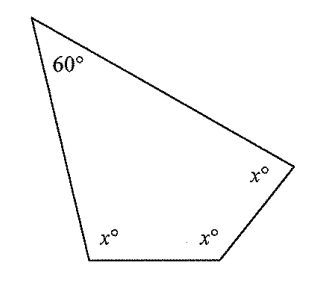
x = 100 degrees
400
What is the equation in standard form of the line that passes through the point (5,2) and is parallel to the line represented by 2x + 5y = 25?
A. 2x + 5y = -20
B. 2x - 5y = 15
C. 2x + 5y = 20
D. 2x + 5y = -15
C. 2x + 5y = 20
400
ABCD is a rhombus. If its diagonals measure 12 cm and 16 cm, what is the perimeter of the rhombus?
Perimeter = 40 cm
400
A quadrilateral has vertices A = (0, 0), B= (1, 3), C = (0, 4) and D = (-1, 1). Prove that ABCD is a parallelogram.
Slope AB = 3 = Slope DC
Slope CB = -1 = Slope DA
Therefore, ABCD is a parallelogram.
400
Consider the figure shown below. If ∠E = (3/4 x + 20), then the value of x is _______? (nearest tenth)
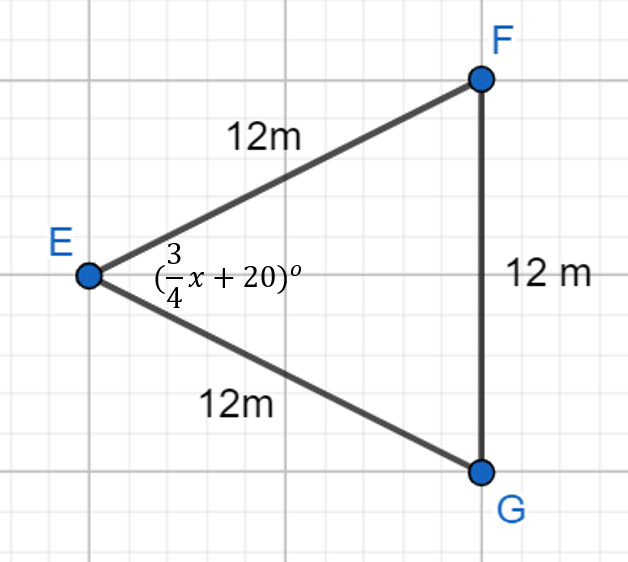
x = 53.3
400
Find the missing Interior Angles. (not to scale)
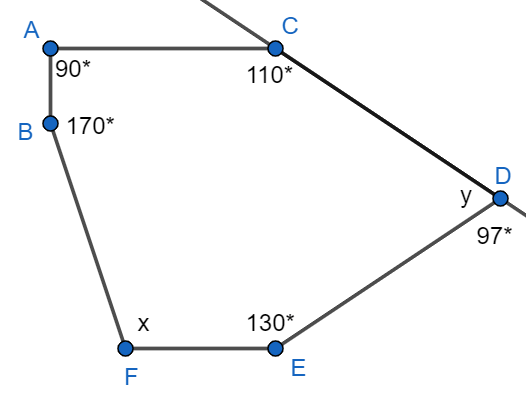
angle x = 137 degrees
angle y = 83 degrees
500
The longer base of a trapezoid has endpoints of (−2,−4) and (4,0). The shorter base contains the point (3,1). What is the equation of the line of the shorter base?
y = 2/3 x - 1
500
On a coordinate grid, Rhonda makes a quadrilateral by connecting the points A(0, 1), B(-1, -2), C(-5, -2) and D(-5, 3).
She knows ∠C is a right angle, she thinks that ∠A might be a right angle, too. Determine if her thinking is correct and provide mathematical evidence to prove if her thinking is correct or incorrect.
Slope DA = -2/5 and Slope AB = 3
Therefore, ∠A is NOT a right angle.
500
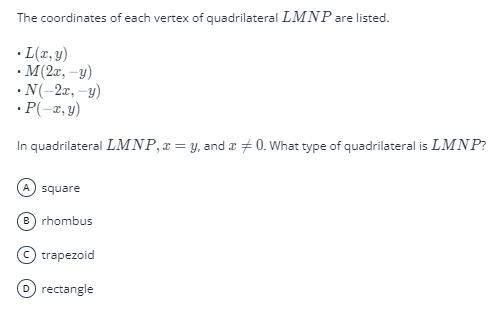
C. Trapezoid
500
In the figure, m∠9 = 80 and m∠5 = 68. Find the measure of each angle. Tell which vocab terms you used.
∠12 = ? ∠1 = ? ∠4 = ? ∠7 = ? ∠16 = ?
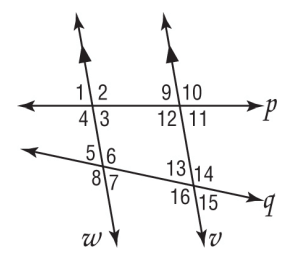
∠12 = 100*, linear pair w/ ∠9
∠1 = 80*, corresponding w/ ∠9
∠4 = 100*, linear pair w/ ∠1
∠7 = 68*, vertical angles w/ ∠5
∠16 =112*, same side interior w/ ∠7
500
The measures of the interior angles of a pentagon are represented by
3x, 2x – 15, 2x + 40, x + 20, and 2x - 35.
What is the measure of the largest interior angle?
x = 53 degrees
3x = 159 degrees