Ch. 6 (Integer Operations)
Ch. 7 (Transformations)
Ch. 8 (Equations and Relationships)
Ch. 9 (Fraction Operations)
Ch. 10 (Angles and Triangles)
100
True or False:
The product of three negative integers is always negative.
True!
E.g. (-2) x (-5) x (-7)
= (+10) x (-7)
= -70
100
Describe the translation, 3 units left, and 7 units up, using algebraic expressions and as a translation vector.
Algebraic Expressions: (x - 3, y + 7)
Translation vector: [-3, 7]
100
Fill-in-the-blank: The ______________ to an equation is the value of the variable that makes the equation true.
solution
100
Convert 43/9 to a mixed number.
4 and 7/9
100
Fill-in-the-blank:
A _______________ is a straight line that intersects two or more parallel lines.
transversal
200
Evaluate -42 and (-4)2. Show the calculations for each to demonstrate why they have different values.
-42 = -1 x 4 x 4
= -4 x 4
= -16
(-4)2 = -4 x (-4)
= +16
200
Describe the translation vector [5, -7] in words.
The translation vector [5, -7] means move 5 units to the right and 7 units down.
200
Collect like terms and simplify the following expression:
4x + 3q + 4 + 7x - 12 - 5q
3q - 5q + 4x + 7x + 4 - 12
= -2q + 11x - 8
200
Convert 11 and 5/8 to an improper fraction.
93/8
200
True or False:
Co-interior angles sum up to 90o.
False!
Co-interior angles sum up to 180o.
300
Evaluate: (-3 - 9)2 x 2 + (-36) ÷ 22
(-3 - 9)2 x 2 + (-36) ÷ 22
= (-12)2 x 2 + (-36) ÷ 22
= 144 x 2 + (-36) ÷ 4
= 288 + (-36) ÷ 4
= 288 + (-9)
= 279
300
The vertex of a point is located at (1, 5) after a reflection in the x-axis.
In which quadrant was the original (i.e. pre-image) point located and what are its coordinates?
The original point was located at (1, -5), which is in Quadrant IV.
300
What is the solution to the following equation?
6 (n + 3) = -2(3 - n)
6 (n + 3) = -2(3 - n)
6n + 18 = -6 + 2n
6n - 2n = -6 - 18
4n = -24
n = -24/4
n = -6
300
Evaluate: 2/3 - 1/4 x 5/6 ÷ 2
2/3 - 1/4 x 5/6 ÷ 2
= 2/3 - 5/24 ÷ 2
= 2/3 - 5/24 x 1/2
= 2/3 - 5/48
= 32/48 - 5/48
= 27/48
= 9/16
300
What type of angles are x and 60o and what is the value of x?
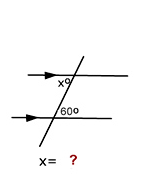
Angle x and 60o are alternate angles, and x = 60o.
400
The sum of two integers is -5 and the difference is 13. What are the two integers?
Let x represent the first integer
Let y represent the second integer
x + y = -5
x - y = 13
+ __________
2x = 8
x = 8 ÷ 2
x = 4
Now, solve for the second integer:
x + y = -5 (4) + y = -5
y = -5 - (4)
y = -9
Therefore the two integers are 4 and -9.
400
△QRS has been dilated by a factor of 1/2. The image triangle has vertices at Q'(3, 5), R'(-4, 1) and S'(7, -6). Where are the coordinates of △QRS located?
Multiply the image coordinates by 2 to find the original (i.e. pre-image) coordinates:
Q(6, 10)
R(-8, 2)
S(14, -12)
400
What is the solution to this inequality?
3x < 5 (x - 1)
If graphing this solution, would you use an open or a closed circle and in which direction would the arrow point (left or right)?
3x < 5 (x - 1)
3x < 5x - 5
3x - 5x < -5
-2x < -5
x > -5 / -2
x > 2.5
If graphing this solution, you would use an open circle and the arrow would point to the right.
400
Use the Pythagorean Theorem to find the value of the longest side length, c, of a right triangle given leg a = 12 cm and leg b = 15 cm. Also, what is the longest side of a right triangle called?
c2 = a2 + b2
c2 = 122 + 152
c2 = 144 + 225
c2 = 369
c = ⎷369
c ≐ 19.21 cm
The longest side of a right triangle is called the hypotenuse.
500
The product of two integers is -48 and their sum is +2. What are the two integers?
List products of -48:
-1 x (+48) = -48
(+1) x (-48) = -48
-2 x (+24) = -48
(+2) x (-24) = -48
-3 x (+16) = -48
(+3) x (-16) = -48
-4 x (+12) = -48
(+4) x (-12) = 48
-6 x (+8) = -48
(+6) x (-8) = -48
Next, select the pair of integers whose sum is +2:
-6 and (+8) because -6 + (+8) = +2
Therefore, the two integers are -6 and +8.
500
Joseph and Jordan play baseball. By the end of their season, Joseph made five more than twice the number of home runs compared to Jordan. Together, they made a total of 41 home runs.
How many home runs did each player make throughout their season?
Let n represent the number of home runs Jordan made
Let 2n + 3 represent the number of home runs Joseph made
n + 2n + 5 = 41
3n + 5 = 41
3n = 41 - 5
3n = 36
n = 36 / 3
n = 12
Next, solve for Joseph's home runs:
2n + 5
= 2(12) + 5
= 24 + 5
= 29
Therefore, Jordan made 12 home runs and Joseph made 29 home runs throughout their season.
500
What is the value of angle x is this diagram. NOTE: Lines CF and GJ are parallel.
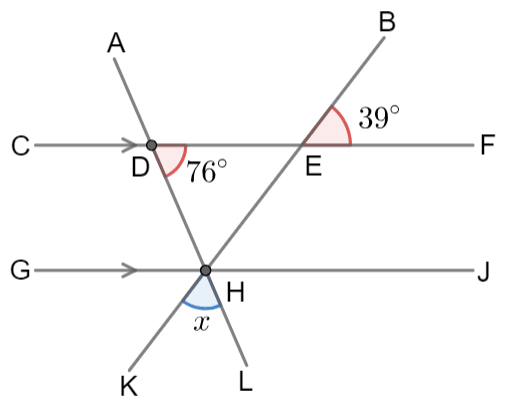
65o