Solving by factoring
Solving by graphing
Vertex form & Transformations
Standard form
100
To solve a quadratic by factoring, you have to set the quadratic equal to what?
You must set the quadratic equal to 0.
100
How many solutions does the quadratic have?
2 solutions
100
What is vertex form for a quadratic?
a(x-h)2+k
100
What is the standard form for a quadratic?
ax2+bx+c
200
Factor and find the solutions.
0=x2+5x-6
x=-6 or x=1
200
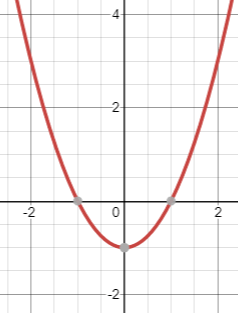
Graph the equation f(x)=x2-1 and find the solutions.
Solutions:
x=-1 or x=1
Graph:
200
What transformation was applied to the quadratic below?
f(x)=(x+3)2
Horizontal translation 3 units to the left.
200
What is the formula to find the axis of symmetry for a quadratic?
x=-b/(2a)
300
Factor and find the solutions.
0=4x2-36
x=-3 or x=3
300
How many solutions does the equation f(x)=x2+2 have?
None.
300
What transformation(s) were applied to the quadratic?
f(x)=-2x2+2
Reflected across x axis.
Shifted up 2.
Vertical stretch by factor of 2.
300
Find the axis of symmetry for the quadratic.
f(x)=x^2+3x+2
x=-3/2
400
Factor and find the solutions if possible.
0=3x2+6x+3
x = -1
400
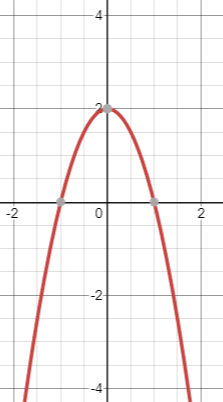
Graph the equation f(x)=-2x2+2. What are the solutions?
Solutions:
x=-1 or x=1
Graph:
400
What kind of transformation(s) were applied to the quadratic?
f(x)=(1/2 x)^2
Horizontal stretch by a factor of 2.
400
What are the steps to find the vertex of a quadratic in standard form?
1. Find the axis of symmetry.
2. Plug the value for the axis of symmetry into the original function.
500
Factor and find the solutions.
0=4x2-20x+25
x=5/2
500
How many solutions does the equation f(x)=-3x2-4 have?
0
500
What is the vertex of the quadratic below?
f(x)=2(x+3)^2-2
(-3,-2)
500
Find the vertex and axis of symmetry of the following quadratic.
f(x)=x2+6x-4
Axis of symmetry:
x=-3
Vertex:
(-3,-13)