Graphing/Writing/Converting Quadratics

Graphs & Equations

100

Does the parabola of the equation below have a maximum or minimum and what is the value?

y=-(x-3)^2-9

Parabola has a maximum since it opens down since a=-1

The y value of the vertex is -9, so

The parabola has a maximum of -9

200

What is the equation of this graph in vertex form?

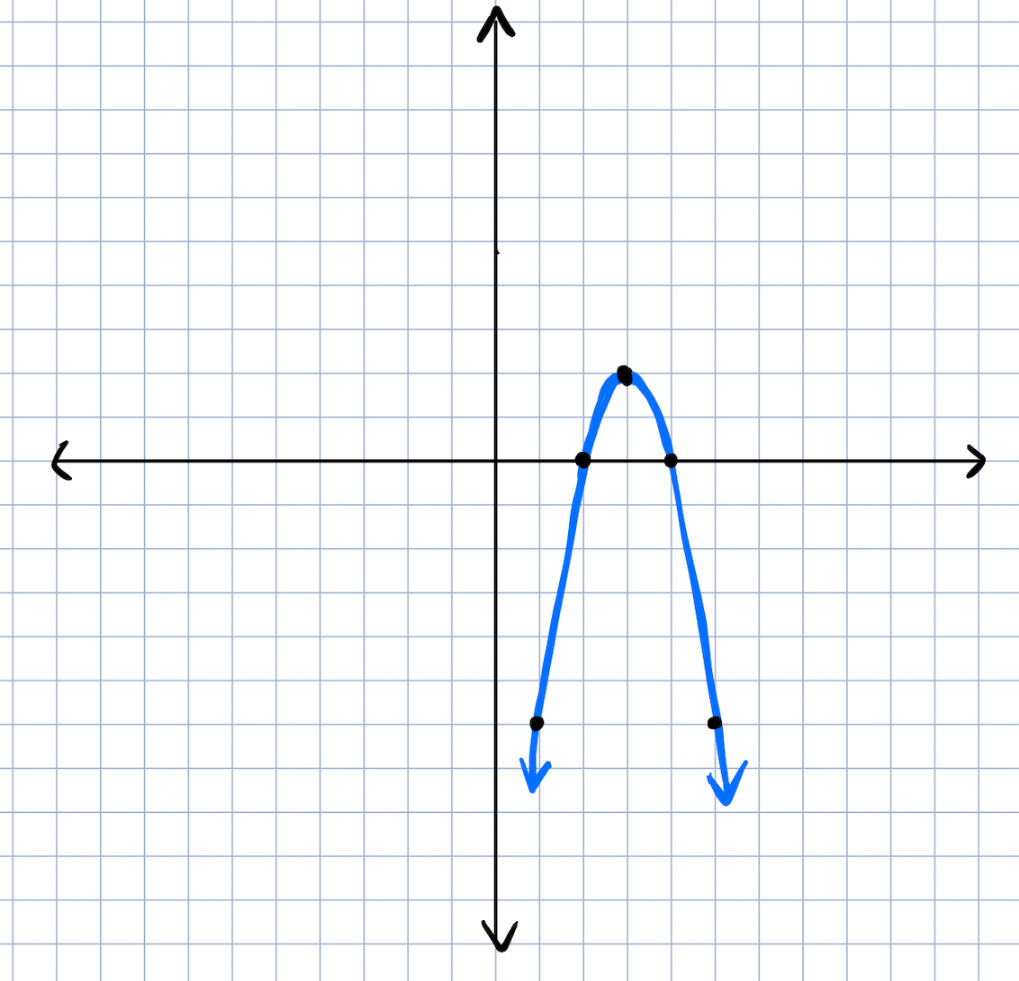
Have vertex so use vertex form

vertex is (h,k):

(3, 2)

a is the slope 1 unit to the right: 

-2

So, the vertex form is:

y=−2(x−3)^2+2

300

What is the equation of this graph in standard form?

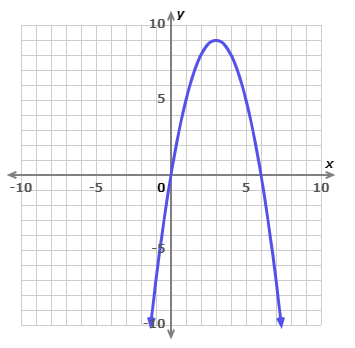
Have vertex so use vertex form, then simplify it to get standard form

vertex is (h,k):

(3, 9)

a is the slope 1 unit to the right: 

-1

So, the vertex form is:

y=−1(x-3)^2+9

Simplify for standard form:

y=−1(x-3)(x-3)+9

y=−1[x^2-3x-3x+9]+9

y=−1x^2+3x+3x-9+9

So, standard form is:

y=−1x^2+6x

400

Write the equation for the graph below in vertex form.

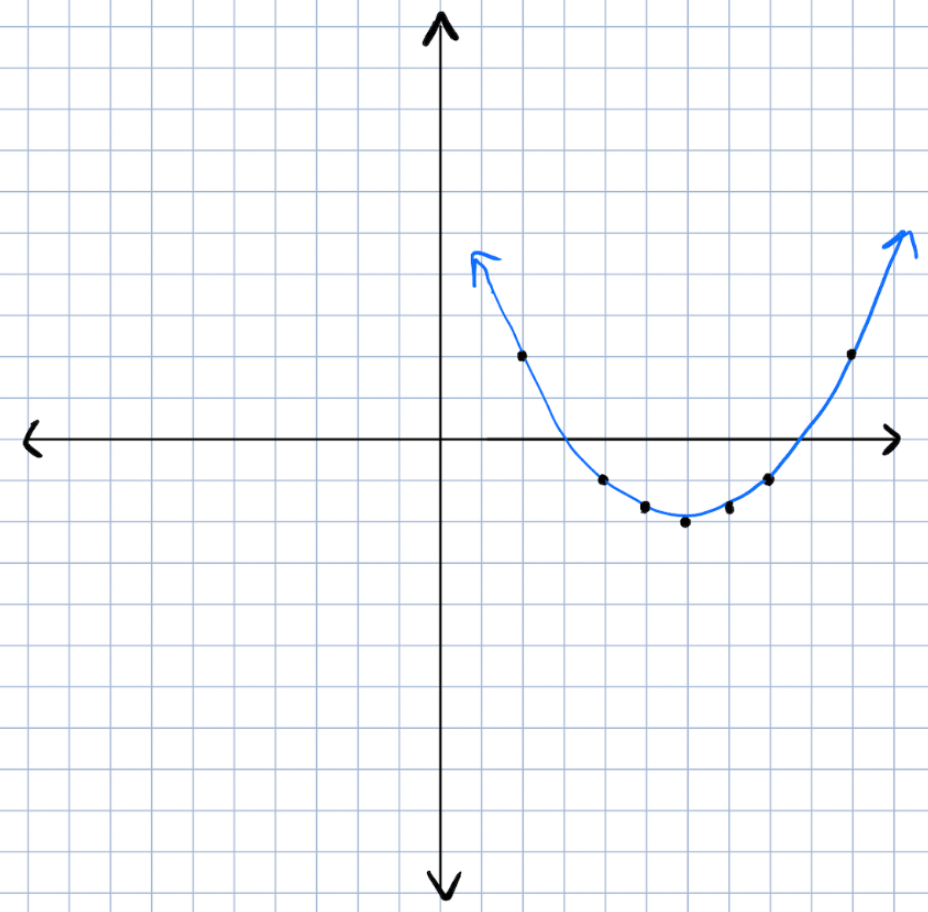
Have vertex so use vertex form

vertex is (h,k):

(6, -2)

a is the slope 1 unit to the right, but we cant tell exactly how far down its going exactly so solve using random (x, y) point: 

Using (4, -1) as (x,y)

-1=a(4-6)^2-2

-1=a(-2)^2-2

-1=4a-2

1=4a

1/4=a

So, the vertex form is:

y=1/4(x-6)^2-2

500

Write the equation in standard form

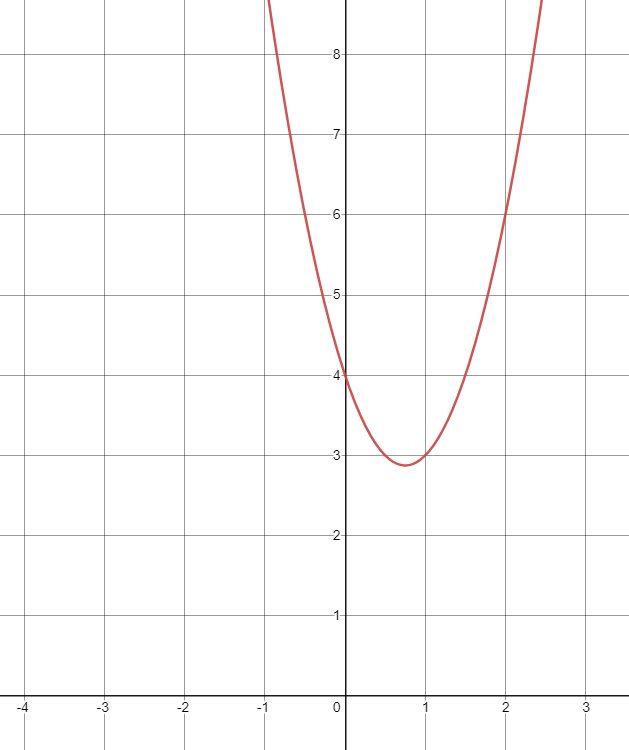
DONT have vertex so use standard form

y-intercept is c:

4

we need to solve for a and b by picking 2 random (x, y) points and making a system of equations with it: 

Using (1, 3) and (2, 6)

{(3=a(1)^2+b(1)+4),(6=a(2)^2+b(2)+4):}

{(-1=a+b),(2=4a+2b):}

{((-1=a+b)(-2)),(2=4a+2b):}

{(2=-2a-2b),(2=4a+2b):}

Add together

4=2a

2=a

Plug in a to find b

-1=2+b

-3

So, the standard form:

y=2x^2-3x+4

Converting Equations

100

Rewrite in standard form. 

y=(x-4)(x+3)+4

y=(x-4)(x+3)+4

y=x^2-4x+3x-12+4

y=x^2-x-8

200

Rewrite in vertex form

f(x)=−2x^2+8x−5

Use a from standard form and find vertex (h, k)

a=-2

h=(-b)/(2a)=(-8)/(2(-2))=(-8)/(-4)=2

k=−2(2)^2+8(2)−5=3

so, vertex form is:

f(x)=−2(x-2)^2+3

300

Rewrite in standard form. 

f(x)=-2(x-1)^2-1

f(x)=-2(x-1)^2-1

f(x)=-2(x-1)(x-1)-1

f(x)=-2[x^2-1x-1x+1]-1

f(x)=-2x^2+2x+2x-2-1

f(x)=-2x^2+4x-3

400

Rewrite in standard form. 

y=1/4(x+1)^2-4

y=1/4(x+1)^2-4

y=1/4(x+1)(x+1)-4

y=1/4[x^2+1x+1x+1]-4

y=1/4x^2+1/4x+1/4x+1/4-4

y=1/4x^2+1/2x-15/4

500

Rewrite in vertex form

f(x)=3x^2+9x+6+3x-7

First simplify to standard form:

f(x)=3x^2+12x-1

Use a from standard form and find vertex (h, k)

a=3

h=(-b)/(2a)=(-12)/(2(3))=(-12)/6=-2

k=3(-2)^2+12(-2)−1=-13

so, vertex form is:

f(x)=3(x+2)^2-13

Intercepts

100

What is the y-intercept?

y=x^2+3x+2

y-intercept in standard form is the "c" value

so, y-intercept is 

2

200

What are your x-intercepts? 

y=x^2-6x+5

To find x-intercepts from standard form set y=0 and solve for x

y=x^2-6x+5

y=(x-1)(x-5)

So, x-intercepts are

1 and 5

300

What are the x-intercepts and the y-intercept?

y=(x+5)(x-7)

From factored form x-intercepts are the p and q values(remember they are opposites)

So, x-intercepts are 

-5 and 7

From factored form the y-intercept can be found by setting x=0 and solving for y

y=(0+5)(0-7)=(5)(-7)=-35

So, y-intercept is

-35

400

Find the x-intercepts

y=-(x+3)^2+4

To find x-intercepts from vertex form set y=0 and solve for x, use the square root method for solving

0=-(x+3)^2+4

-4=-(x+3)^2

4=(x+3)^2

+-2=x+3

x=-3+-2

So solutions are

-3+2 and -3-2

-1 and -5

500

Find the y-intercept

f(x)=3(x+2)^2+2

To find y-intercept from vertex form set x=0 and solve for y

f(0)=3(0+2)^2+2

f(0)=3(2)^2+2

f(0)=3(4)+2

f(0)=12+2

f(0)=14

So, y-intercept is

14

Vertex & A.O.S

100

Find the axis of symmetry.

f(x)=(x+1)^2-8

Axis of symmetry is the vertical line down x-value of vertex "h":

x=-1

200

Find the vertex

y=(x-3)^2+4

From vertex form, vertex is (h, k)

so, vertex:   (3, 4)

300

Find the axis of symmetry.

y=x^2-4x-5

Axis of symmetry is the vertical line down x-value of vertex "h", in standard form 

h=(-b)/(2a)

h=(-(-4))/(2(1))=4/2=2

So, A.O.S.:   x=2

400

Find the vertex.

y=3(x-4)(x+16)

Vertex from factored form (h,k) find h using formula below, then plug in to find k.

h=(p+q)/2

h=(4+ -16)/2=(-12)/2=-6

k=3(-6-4)(-6+16)=3(-10)(10)=-300

so, vertex:   (-6, -300)

500

Find the vertex.

y=1/2x^2+3x+4

Vertex from factored form (h,k) find h using formula below, then plug in to find k.

h=(-b)/(2a)

h=(-3)/(2(1/2))=(-3)/1=-3

k=1/2(-3)^2+3(-3)+4=-1/2

so, vertex:   (-3, -1/2)