Graphing Systems
Substitution
Parallel and Perpendicular
True or False
100
What is the solution of this system of equations?
(2, 2)
100
Solve using substitution:
y=1
2x + y = 11
(5, 1)
100
The slopes of parallel lines are...
The same (or equal)
100
A system of equations means that the equations will always have a solution.
False
200
What is the solution to this system of equations?
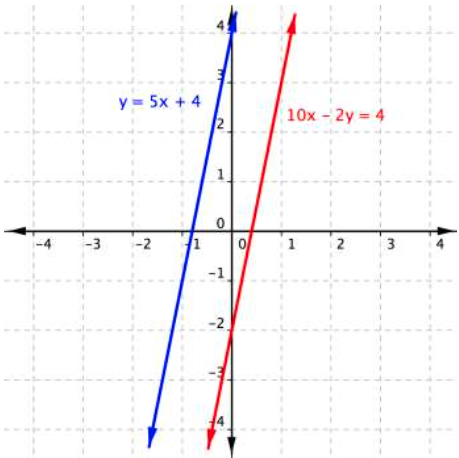
NO SOLUTION
200
Solve using substitution:
y = 2x
x + 2y = 30
(6, 12)
200
The slopes of perpendicular lines are...
Opposite reciprocals
Opposite signs and flipped fractions
200
Perpendicular lines have the SAME slope
False
300
Explain why (0, -1) is the solution for this system of equations.
It is the point where the lines intersect/meet.
300
Solve using substitution:
y = x + 3
y + 3x = 19
(4, 7)
300
Write an equation that would be PARALLEL to
y = 4x - 1
Anything with a slope of 4 and a different y-intercept
(Ex: y = 4x + 2)
300
This system of equations has infinite solutions:
y = -2x + 5
2x + y = 5
True
400
DRAW a system of equations that would have the solution (0, 1).
answers vary
400
x = 2y + 1
3x - y = 13
(5, 2)
400
Write the equation of a line that would be PERPENDICULAR to
y = 4x - 1
Anything with a slope of -1/4
(Ex: y = -1/4x + 3)
400
If two lines are PARALLEL, the system of equations has INFINITE SOLUTIONS.
FALSE, NO SOLUTION
500
Rewrite this equation in slope-intercept form (y=mx+b):
5x +3y = 6
y = -5/3x + 2
500
Solve using substitution:
2x - y = 8
y = -x - 2
(2, -4)
500
True or false: Perpendicular lines have infinite solutions.
False: One solution
500
Emma was solving this system of equations using substitution. She got 4x = 0 and said there was NO SOLUTION. Is this true?
y = 2x
2x + y = 0
FALSE. She can divide both sides by 4 to get x = 0.