Graphs

Level One

100

Why is the running time of O(m+n) the same as O(m) for undirected connected graphs?

m >= n -1 

200

When does DFS compute the shortest path? When does BFS compute the shortest path? (Undirected graph)

DFS doesn't compute the shortest path. It only computes the nodes reachable from the start node. 

BFS computes the shortest path for an unweighted graph are when all edge costs are equal

300

What is the time complexity for examining all edges incident to a given node?

theta(n) 

400

When is an undirected graph a tree? How many edges does it have?

When it is connected and does not contain a cycle which mean it has n-1 edges

500

For any connected graph G=(V,E) there is always a start vertex s∈V, such that there is always at least two distinct BFS trees possible when starting the BFS at s.

False 

600

Every directed graph on n vertices that has no cycles has at most n−1 edges.

False. If there is a cycle there will me at least n nodes

Midterm 1

100

Consider the BFS algorithm with its input graph G in adjacency list format. Argue why the input size for BFS is s Θ(n +m)

This is because the adjacency list representation takes Θ(m +n) space (as we saw in class when we compared the adjacency matrix and adjacency list representations).

200

Is the following statement true or false? Also remember to briefly JUSTIFY your answer. BFS is a linear time algorithm. 

(Recall that an algorithm is a linear time algorithm if it runs in time O(N) on inputs of size N.)

True. Recall that we have shown that BFS runs in time O(m + n) when the graph is represented in the adjacency list format. Further, from part 1, N = Θ(n +m), which implies the run time is O(N)

Note: Ask TA for further explanation

300

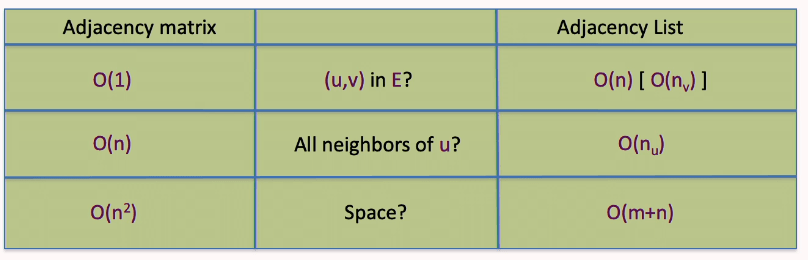
For any graph, recall that running the BFS algorithm implicitly computes a BFS tree. (Note: BFS tree is not rooted.) (Part 1) Argue why the following statement is TRUE. A BFS tree can be computed (explicitly) in O(m +n) time

See the BFS pseudocode in the textbook for the algorithm. 

400

Is the following statement true or false? Also remember to briefly JUSTIFY your answer. 

Every graph has a a unique BFS tree for it.

FALSE

500

(Part 1) Argue why the following statement is TRUE. A directed graph has at most n² edges in it.

Since there are n² pairs of vertices, any directed graph has at most n² edges

600

(Part 2) Is the following statement true or false? Also remember to briefly JUSTIFY your answer. 

Any directed graph on n vertices with at least n −1 edges is strongly connected.

False. Consider the following DAG on three vertices A,B,C with directed edges (A,B), (B,C), (A,C). In this graph C is not connected to A but it has n = 3 edges

Connectivity in Directed Graphs

300

How are directed graphs related to undirected graphs?

Every undirected graph can be a directed graph.

Midterm 2

100

(Part 1) Argue why the following statement is TRUE. Adjacency matrix takes Θ(n 2 ) space.

This was stated in the lecture were we compared adjacency matrix and adjacency list representation of graphs

200

True or False: Every DAG on n nodes has O(n²) edges in it?

Follows from part of Q1(g) on sample mid-term-1

300

When we work with undirected connected graphs, why is a running time of O(m+n) the same as O(m)?

m>= n -1

400

Let G = (V,E) be an undirected graph such that every vertex has degree greater than or equal to 13. Then G has a cycle in it.

True or False

True

500

Is the following statement true or false? Also remember to briefly JUSTIFY your answer. 

There is an O(n²) time algorithm that for any graph on n vertices given in its adjacency matrix, converts it into its adjacency list representations.

True. In short here is the algorithm: go through the matrix row by row and for the vertex u corresponding to the current row, add a list of vertices w such that the entry for (u,w) is a 1. Each row takes O(n) time and there are n rows, which makes for a total running time of O(n²).

600

What are the requirements for Dijkstra's algorithm?

Integer edge lengths and non-negative edge costs