¿Cuál es el mcm de 2 y 3?
6
¿Cuál es el mcm de 5 y 6?
30
¿Cuál es el MCD de 8 y 12?
4
Cierto o falso:
Un cilindro oblicuo es un ejemplo sólido de revolución.
Falso, por no tener un eje perpendicular con la base.
Nombre del poliedro cuyas caras son triangulares y, al unirlas, terminan en una cúspide.
Pirámide
Sólido de revolución, cuya generatriz es un rectángulo:
cilindro
Nombre del siguiente sólido geométrico:

cono truncado
Cierto o falso:
Todos los poliedros pueden formar sólidos de revolución.
Falso, solo los no poliedros lo hacen: cono, cilindro y esfera.
¿Qué se forma al hacer girar la siguiente banderita?

Un cono recto.
Cierto o falso:
Todos los cuerpos en 3D son poliedros.
Falso, ya que la esfera, cilindro y cono no lo son.
¿Qué se forma al armar el siguiente desarrollo plano?
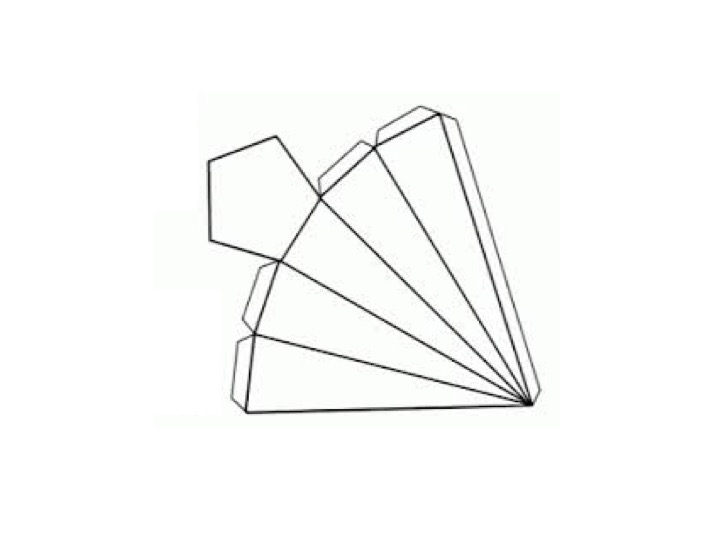
Una pirámide pentagonal
Nombre del segmento donde coinciden las caras de un sólido tridimensional:
arista
Nombre del siguiente sólido geométrico:
tetraedro
Nombre de la recta perpendicular que divide a un sólido de revolución exactamente en su mitad:
eje de simetría
Poliedro regular cuyas caras son redondas y no tiene vértices:
No existe este sólido porque los único sólido sin vértices son el cilindro, cono truncado y esfera y estos no son poliedros.
¿Cómo se calcula el largo de un cilindro para que encaje perfectamente con sus bases circulares?
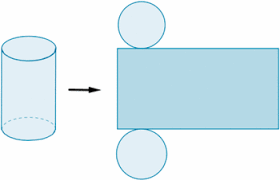
2 * pi * r
Nombre de la línea que, al girar alrededor de un eje, da lugar a un sólido de revolución:
generatriz
Lugar en el que coinciden las aristas:
Menciona dos poliedros regulares:
cubo o hexaedro; tetraedro; octaedro; dodecaedro; icosaedro
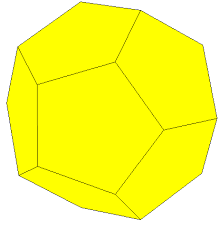
Nombre del poliedro, cuyas caras son todas pentágonos regulares:
Dodecaedro, observa:
Menciona cinco sólidos platónicos:
cubo o hexaedro, tetraedro, octaedro, dodecaedro e icosaedro.
Nombre del poliedro que tiene las siguientes características:
* 2 bases cuadrangulares
* 4 caras rectangulares
* 8 vértices y
* 12 aristas
prisma cuadrangular, observa:

Menciona 5 ejemplos donde se apliquen los sólidos de revolución en la vida cotidiana:
elaboración de botellas, barriles, tazas, vasos, cerámica, taladro, patinaje profesional, etc.
Menciona el procedimiento para conocer cuántos divisores tiene un número:
2. Se representa en potencias sus productos.
3. Se suma 1 al exponente de cada potencia.
4. Se multiplican los números obtenidos en el paso 3 y el resultado, equivale al número de divisores totales.
El rey Midas tiene 120 monedas de oro y 144 de plata. Quiere colocarlas en torres que contenga tanto monedas de oro como monedas de plata, todas con el mismo número de monedas. ¿Cuál es el mayor número de elementos que puede tener cada torre?

Se obtiene el MCD (120, 144)= 24, por lo tanto, cada torre debe tener 24 monedas.
Porción de un círculo delimitado por dos radios y un arco de circunferencia:
sector circular
18 y 24:
mcm= 72
MCD=6
Menciona cómo se relaciona la química con las matemáticas, (haz referencia a lo que aprendimos este mes).
Con la forma geométrica de las moléculas.
Nombre del siguiente cuerpo geométrico:

octaedro irregular
En una máquina, un engrane con 96 dientes se asocia con uno de 45 dientes, ¿cuántas vueltas da el engrane chico hasta que coinciden de nuevo los puntos A y B? Explica como lo calculaste.
El engrane chico debe dar 32 vueltas pues se tiene que el mcm (96,45)=1440, así que se divide:
1440/45 =32