Chapter 1
Chapter 2
Chapter 3
Word Problem Practice
Random
100
Write a recursive formula for the nth term of the arithmetic sequence:
34, 37, 40, 43, . . .
u1 = 34
un = un-1 + 3
100
Solve the system:
11x-6y=3
5x-8y=-25
(3,5)
100
Is the following a function? Why or why not?
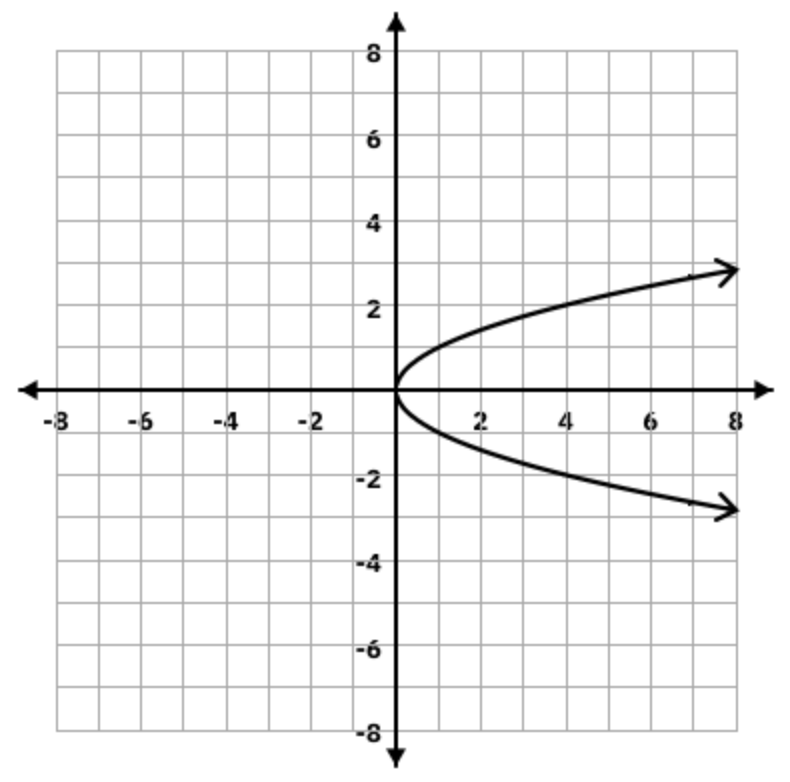
No, it doesn't pass the vertical line test
100
The EP Drama Club is selling tickets to the annual Broadway Extravaganza. As a way to encourage EP residents of all ages to attend the event, senior citizen tickets and child tickets are sold at reduced prices. On the first day of ticket sales, the club sold 3 senior citizen tickets and 5 child tickets for a total of $70. On the second day of ticket sales, the club sold 12 senior citizen tickets and 12 child tickets for $216.
Let x= the cost of a senior citizen ticket and y= the cost of a child ticket.
Write a system of equations to represent the situation.
3x+5y=70
12x+12y=216
100
Solve for y:
3x+2y<10
y<-3/2x+5
200
Write a recursive formula for the nth term of the geometric sequence:
12, 18, 27, 40.5,. . .
u1 = 12
un = 1.5 • un-1
200
Solve the system:
2y=-3x
y=-2x+2
(4, -6)
200
Let f(x)=x^2-3 and g(x)=x+5 .
Find f(x)-g(x) .
x^2-x-8
200
You invest $4000 into an account that earns 1.5% interest compounded annually.
Write a recursive formula that describes the situation. Use u0 to represent the starting term.
u0 = 4000
un = (1.015)un-1
200
What is the vertex of the function:
y=|x+4|+3
(-4,3)
300
Consider the arithmetic sequence defined by the formula:
u0 = 3.6
un = un-1 - 6
Write an explicit formula for the sequence.
un = -6n + 3.6
300
Solve the system:
2xy=12
xy+y=8
(3,2)
300
Use the graph to find the value f(f(5))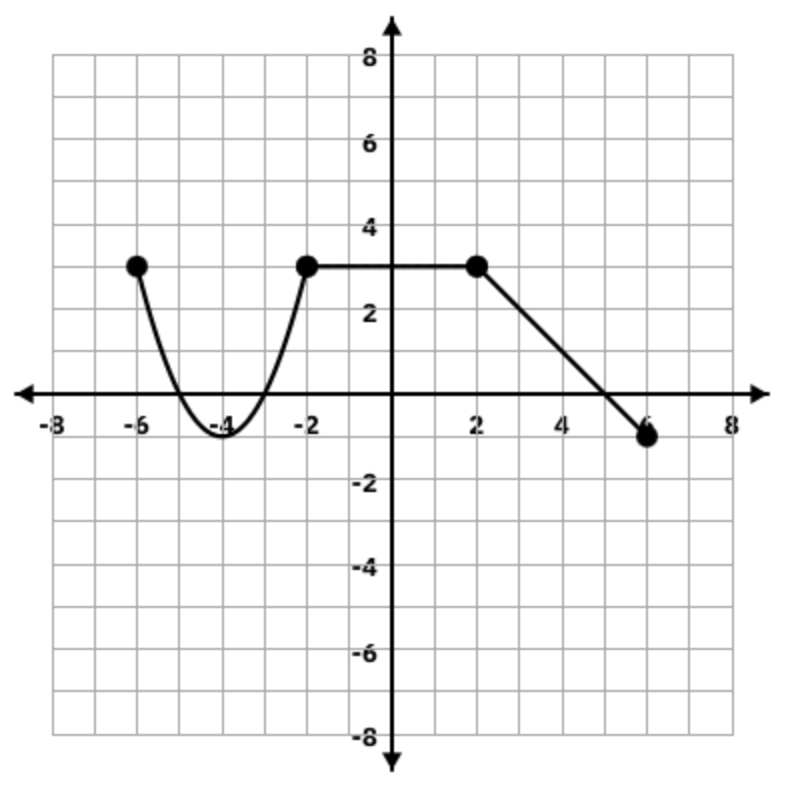 
3
300
A math quiz has 25 questions. Some questions are worth 1/4 of a point and others are worth 1/2 a point. There are a total of 9 points on the quiz.
Write a system of equations to represent the situation.
x+y=25
1/4x+1/2y=9 OR .25x+.5y=9
300
Solve for y:
-3x-3y≥9
y≤-x-3
400
Write the explicit rule for the nth term. Let u1=34.
34, 37, 40, 43,. . .
Then find the 32nd term.
Explicit rule: un=dn+u0
un = 3n+31
u32 = 127
400
Solve the system:
y=x-7
y=8/x
(8,1) and (-1,-8)
400
Write the equation of a parabola with vertex (2,-1) passing through the point (-2,47).
Hint: don't forget to find a.
y=3(x-2)^2-1
400
A calculator company produces a scientific calculator and a graphing calculator. Long-term projections indicate an expected demand of at least 100 scientific and 80 graphing calculators each day. Because of limitations on capacity, no more than 200 scientific and 170 graphing calculators can be made daily. To satisfy a shipping contract, a total of at least 200 calculators must be shipped each day.
If each scientific calculator sold results in a $2 loss, but each graphing calculator results in a $5 profit, how many of each type should be sold to maximize profits?
Let x=scientific calculators and y=graphing calculators.
Write an objective quantity statement.
P = -2x + 5y
400
Solve for x:
-5sqrt(x+1)+12=2
x=3
500
Consider the graph of the sequence. Write an explicit rule.
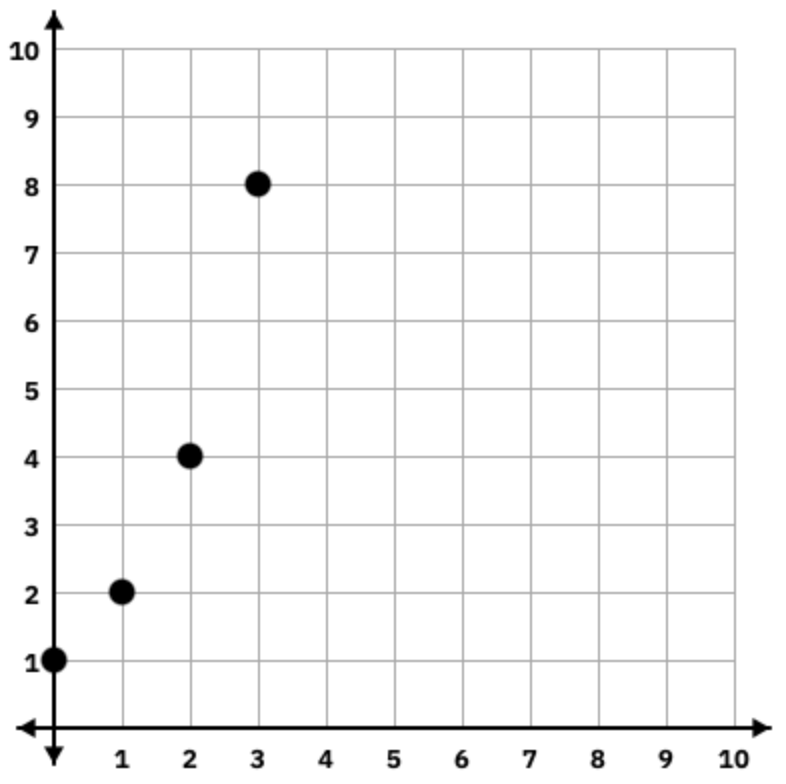
Explicit rule: un = u0(r)n
un = (2)n
500
Solve the system:
2x-4y+2z=16
-2x+5y+2z=-34
x-2y+2z=4
(8,-2,-4)
500
Find f(g(x)) :
f(x)= root 5 (x-1)
g(x)=x^5+1
x
500
A calculator company produces a scientific calculator and a graphing calculator. Long-term projections indicate an expected demand of at least 100 scientific and 80 graphing calculators each day. Because of limitations on capacity, no more than 200 scientific and 170 graphing calculators can be made daily. To satisfy a shipping contract, a total of at least 200 calculators must be shipped each day.
Let x=scientific calculators and y=graphing calculators.
Write a system of constraints.
x≥100 and x≤200
y≥80 and y≤170
x+y≥200
OR
100≤x≤200
80≤y≤170
x+y≥200
500
Given the function:
f(x)=(x-4)^2+2
Find the domain and range.
Domain: (-infty, infty)
Range: [2, infty) or y≥2