3.1 Conjectures and Counterexamples
3.2 Statements, Conditionals, and BiConditionals
3.3 Deductive Reasoning
3.4 Writing Proofs
PotPourri
100
Making a conjecture is a part of applying _____________ reasoning.
inductive
100
Identify the hypothesis and conclusion of the following conditional:
If you do not pray, then you will not be saved.
Hypothesis: you do not pray
Conclusion: you will not be saved
100
The law that tells us: given "if p, then q" and "p", we can conclude "q" is called the:
Law of Detachment
100
The property that tells us we can switch what is on each side of an equation is called the:
Symmetric Property of Equality
100
If p is true and q is true, what is the truth value of:
~p v q
true
200
True or false. If false, give a counterexample.
If a shape is a quadrilateral, then it is a square or rectangle.
Trapezoid, Rhombus, Etc.
200
Write a true conditional with a false hypothesis and true conclusion.
Example: If Mr. Ensey is the pope, then 1+1=2
200
The law that tells us if we are given "if p then q" and "if q then r", we can conclude "if p then r" is called the:
Law of Syllogism
200
Suppose we had these steps:
Step 5: 4 + 5x + 8 = 2x - 8 + 8
Step 6: 12 + 5x = 2x
What is the reason for step 6?
Substitution
200
If the hypothesis of a conditional statement is false, then the entire conditional is (true/false)
True!
300
True or False? If false, give a counterexample.
If x^2 =25, then x = 5.
False. Counterexample: x = -5
300
A biconditional is the combination of a ___________________ and a ______________________.
conditional, converse
300
Make a valid conclusion using the law of detachment or the law of syllogism, if possible. If not, say "no valid conclusion" and explain.
If tomorrow is Friday, then today is Thursday.
If today is Thursday then yesterday was Wednesday
Valid Conclusion: If tomorrow is Friday, then yesterday was Wednesday.
300
The Step "Combine Like Terms" or "Simplify" we call what?
Substitution
300
An OR statement is called a ____________.
An AND statement is called a _____________.
disjunction, conjunction
400
Given the sequence 1, 4, 9, 16...
Make a conjecture about the pattern and find the next term in the sequence.
Example: These are the perfect squares; the next term is 25.
400
When the last statement of a truth table is all true, we call it a _________________.
When the last statement of a truth table is all false, we call it a ___________________.
tautology, contradiction
400
State the Law of Detachment.
If "if p then q" is true and "p" is true, then "q" is true.
(If given "if p then q" and "p", we can conclude "q", assuming "if p then q" and "p" are true")
400
When do we use the reflexive property in a proof?
We use the reflexive property because we need to show that what we are about to add/subtract/multiply/divide (on both sides of the equation) is actually the same thing.
400
Suppose that a conditional was written as w→ z.
Tell me in words what the symbols would be for the following...
converse
inverse
contrapositive
converse: z → w
inverse: ~w→ ~z
contrapositive: ~z→ ~w
500
Make a conjecture about the sum of three prime numbers. Give three examples to back up your claim.
The sum of three prime numbers is an odd number.
1+3+5 =9
5+5+5=15
7+11+13=31
500
Write a truth table for this statement.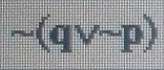 
Mr. Ensey will check.
5 columns: p, q, ~p, (q V ~p), ~(q V ~p)
500
The law of logic "Modus Tollens" tells us if we are given "if p then q" and "~q", we can conclude "~p".
If water reaches a temperature of 0 degrees Celsius, then it will freeze.
Water will not freeze.
What is a valid conclusion?
Water does NOT reach a temperature of 0 degrees Celsius.
500
Write the following proof on your paper. Then show me what you wrote down using your camera to answer.
Given:5(x+1) = 30
Prove: x = 5
5(x+1)=30 (Given)
5x+5=30 (Distributive Property)
5=5 (Reflexive POE)
5x+5-5=30-5 (Subtraction POE)
5x=25 (Substitution)
5=5 (Reflexive POE)
5x/5=25/5 (Division POE)
x=5 (Substitution)
500
Give ALL the counterexamples for the following statement:
"If x > 0, then x > 1."
Any number between 0 and 1, including 1.