Linear Equations
Functions
Slope
Inequalities
Transformations
100
-20 = x - 5
x = -15
100
f(x) = 4x - 2
Find f(x) when x = -3
f(-3) = -14
100
Find the slope of these two points:
(-2, 5) and (0, 2)
-3/2
100
3x > -9
x > -3
100
Translate (0, -7) using the vector <-3, -1>
(-3, -8)
200
-10 - 7n = -3
n = -1
200
f(x) = 4x - 2
Find x when f(x) = 18
x = 5
200
In the equation y = mx +b, the variable ___ represents the slope.
m
200
4(-x - 1) < 12
x > 16
200
Reflect (4, 2) across the y-axis
(-4, 2)
300
x/3 - 7 = -4
x = 9
300
f(x) = 4x -7
Find f(2)
f(2) = 1
300
Identify the slope
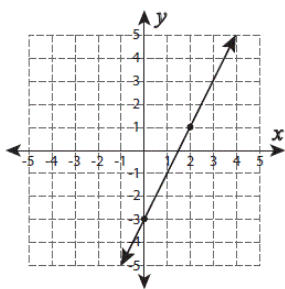
2
300
x - 4 > -5x + 11
x > 15/6
300
Reflect (-10, -12) across y=x
(-12, -10)
400
-6(4x + 7) = 30
x = -3
400
f(x) = 2(x-2) + 7
Find f(3)
f(3) = 9
400
Identify the slope.
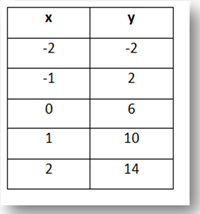
4
400
Write an inequality to represent the word problem:
Three times the sum of two and a number less than fifteen.
3(2 + x) < 15
400
Rotate (-2, 1) 270 degrees counterclockwise
(1, 2)
500
3(x + 12) = 4(x - 1)
x = 40
500
f(x) = -3 + 9x
Find x when f(x) = -13
x = -10/9
500
Given the table, find the slope of the table
m = 3/1 or 3
500
Write an inequality to represent the word problem:
Andy wants to buy school supplies with $42. He wants to buy a backpack that costs $25 and notebooks that cost $3.50 each. How many notebooks can Andy buy?
42 ≥ 25 + 3.5n
0≤ n ≤ 4
500
Translate A(-2, 4) using (x, y) --> (x+9, y-4)
Then rotate A' 180 degrees
(-7,0)