Vocabulary
All About Scale
Proportional Relationships
Proportional Relationships and Equations
Proportional Relationships and the Coordinate Plane
100
The point (0,0) on a coordinate plane
Origin
100
The number you multiply by to get a scale copy
Scale Factor
100
What is the only operation used when finding proportional relationships?
Multiplication!
100
What is the equation for a proportional relationship?
y=kx
100
What are the two requirements for a graph of a proportional relationship?
1. Straight line
2. Goes through the origin (0,0)
200
The values for one quantity are each multiplied by the same number to get the values for the other quantity.
Proportional Relationship
200
Original Length: 15 cm
New Length: 5 cm
What is the scale factor?
1/3
(15* 1/3 = 5)
200
Does this table show a proportional relationship?
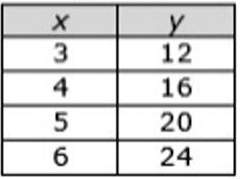
Yes
(Constant of Proportionality: 4)
200
What does the k in the proportional relationship equation y=kx represent?
Constant of Proportionality
200
Does this graph show a proportional relationship?
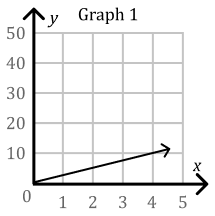
Yes
(k=2.5)
300
The number used to multiply the values of one quantity to get the values for the other quantity
Constant of Proportionality
300
Original Length: 9 in.
Scale Factor: 6
What is the new length?
54 in.
(9*6=54)
300
Find the missing value
20
300
What is the equation for the proportional relationship shown below?
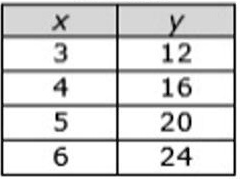
y=4x
300
Does this graph show a proportional relationship?
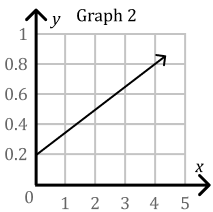
No
(Does not start at the origin)
400
A copy of a figure where every side length in the original figure is multiplied by the same number.
Scale Copy
400
Are these shapes scale copies?
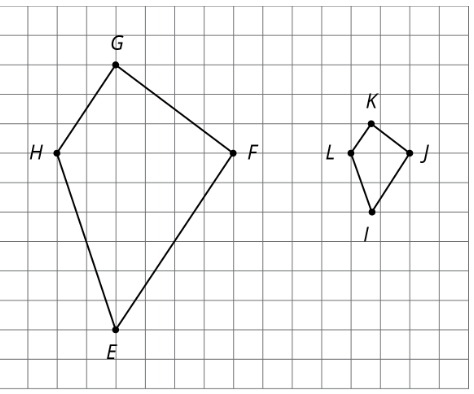
Yes
(Scale factor: 1/3)
400
What is the constant of proportionality between the number of mules and bales of hay?
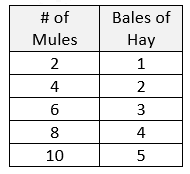
1/2
(Ex: 4*1/2=2)
400
Eddie loves to wear socks with crazy patterns. He finds a great deal for some socks at his favorite store. Eddie buys 15 pairs of socks for $30. What is the equation to represent the price of a pair of socks?
y=2x
(Equivalent variables are acceptable)
400
Which line represents the person who walked faster?
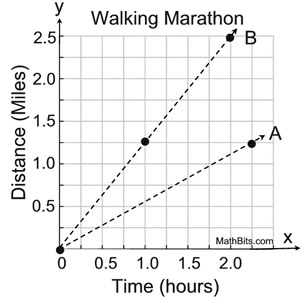
Line B
(Steeper line = larger constant = faster speed)
500
Two numbers that multiply to equal 1.
Reciprocal
500
Are these shapes scale copies?
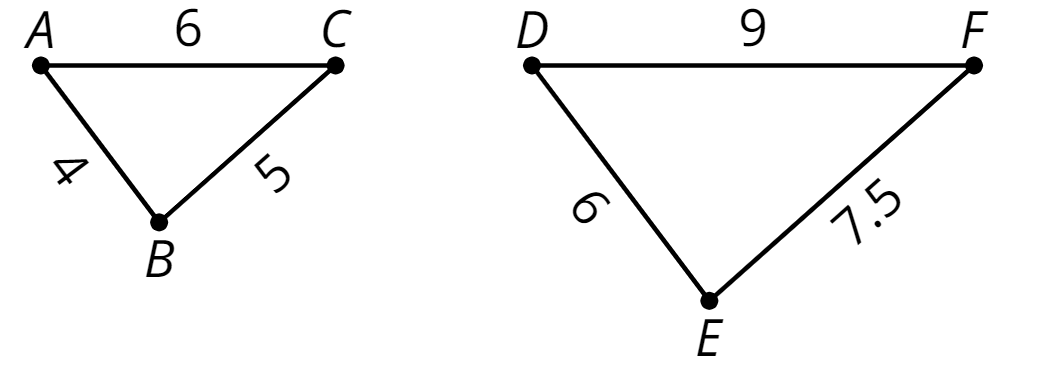
Yes
(Scale Factor: 1.5)
500
Barry is baking cakes for a party. The recipe calls for 3 cups of flour and 2 cups of sugar. How much sugar will be needed if Barry uses 12 cups of flour for his cakes?
8 cups of sugar
500
How can you use the proportional relationship equation to find the constant of proportionality?
y/x=k
500
What coordinate point can I use to find the constant k?
(1,y)