Coin Flips
Waiting For It
Adding Up the Wins
Roll of the Die
What a Formula!
100
Let X be a Bernoulli(1/4) random variable. The probability that X is equal to 0.
What is 3/4?
100
The probability that a Geometric(1/4) random variable is equal to 2.
What is 3/16?
100
Let X be a Binomial(3,3/4) random variable. The probability that X is greater than 0.
What is 63/64?
100
Let X be a Discrete Uniform(1,9) random variable. The probability that X is odd.
What is 5/9?
100
The mean of a Poisson(3) random variable.
What is 3?
200
The average value of a Bernoulli(0.317) random variable.
What is 0.317?
200
The probability that a Geometric(1/4) random variable is greater than 2.
What is
1 - (\frac{1}{4} + \frac{1}{4}\cdot\frac{3}{4}) = \frac{9}{16}
200
Let X be a Binomial(4,1/2) random variable. The probability that X is greater than 2.
What is 5/32?
200
Let X be a Discrete Uniform(2,4) random variable. The expected value \mathbb{E}[2X+1]
What is
2\mathbb{E}[X] + 1 = 2\cdot3 + 1 = 7
200
The probability that a Poisson(3) random variable is less than 2.
What is
4 e^(-3)?
300
Let X be a Bernoulli(1/2) random variable. The value of \mathbb{E}[X^2]
What is 1/4?
300
Let X be a Geometric(1/2) random variable. The value of \mathbb{E}[X^2]
What is
\mathbb{Var}[X] + (\mathbb{E][X])^2
=\frac{1-\frac{1}{2}}{(\frac{1}{2})^2} + (\frac{1}{2})^2 = \frac{9}{4}
300
Let X be Binomial(100,0.1). The value of Var[2X - 5]
What is 36?
300
Let X be a Discrete Uniform(51,54) random variable. The variance of X.
What is 15/12?
300
Let X be a Poisson (\lambda) random variable satisfying \mathbb{E}[X - 1] = 1 . The value of the parameter \lambda
What is 2?
400
Let X be a Bernoulli(2/3) random variable. The value of \mathbb{E}[3^X]
What is 7/3?
400
Let X be a Geometric(1/2) random variable. The probability that X is greater than 4, given that we know that X is greater than 2, \mathbb{P}[X > 4 | X > 2] .
What is 1/4?
400
You play 5 games in a row. The probability that you win a game is 1/2, independently of other games. Let X be the number of wins and B = \{0,1\} . The conditional PMF of X given that \{X \in B\} occurs.
400
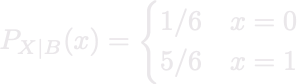
Let X be a Discrete Uniform(1,87) random variable and let B = \{2,3,4\} .
The conditional PMF P_{X|B}(x) of X given \{X \in B\}
400
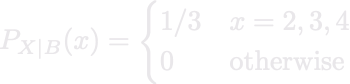
Let X be a Poisson(2) random variable. Given that X is less than 3, what is the probability that X is equal to 0?
What is 1/5?