Solve for x.
2x > 8
x > 4
True or False
When solving inequalities, flip the sign when multiplying both sides by a negative. Do not flip the sign when dividing both sides by a negative.
FALSE!!!!!
Flip the sign when multiplying or dividing both sides by a negative.
Solving Inequalities
4 < f + 6 < 5
What is:
-2 < f < -1
When solving absolute value equations and inequalities, you must first ISOLATE the absolute value. In other words, get the absolute value by itself.
Solve:
|x - 4 | < 4
What is
0 < x < 8
x>0 AND x<8
Solve
X + 4 < -88
X < -92
Solving Inequalities
Solve for x.
2x - 5 > - 11
x > -3
Graph the inequality:

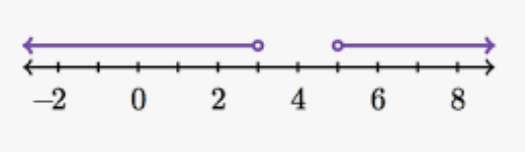
True or False?
-4 is included in the solution of
x > -20.
True.
-4 is greater than -20.
- 4 > -20
Solve:
3|c - 2| > 6
c < 0 OR C > 4
x/-5>2
x<-10
-4x+1>5
x<-1
Graph the inequality:
0<=x<3
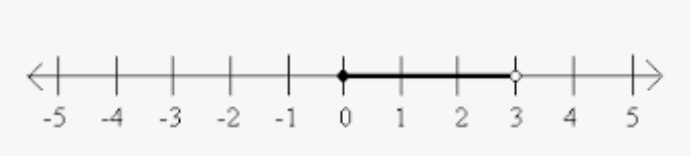
True or false:
If the variable is on the left side of the inequality and getting pointed to, shade right.
False.
If the variable is on the left side of the inequality and getting pointed to, shade left.
How would you rewrite the inequality to make the relationship make more sense for graphing?
-1>x> -5
-5<x< -1
z/30>70
Solve the Inequality
z > 2,100
Is 3 included in the solution to this inequality?
-9x + 1 > -71
Yes, because x must be less than 8.
Solve
-3p + 1 < -11 OR p + 4 < 6
p > 4 OR p < 2
True or False:
We use a closed circle to represent the inequalities < and >.
False
|2y - 9 | = 1
y = 5
y = 4
Solve the Inequality:
x-20 le -58
x le -38
Solve the inequality
11 < 2 - 3x
x < -3
or
-3 > x
-12 < -3x + 6 < -6
6 > x > 4
True or False: These two statements are the same
1<=x<4
1<=x and 4<x
False.
1<=x<4
Evaluate
|2x-4|<-2
No solution due to the fact that the absolute value cannot be less than a negative number.