Solve for the variable x:
5x - 4(2x - 3) = 18
x=-2
Solve for the variable x below:
x + 3(2 - x) > 20
x<-7
Graph the equation on the coordinate plane:
y=1/2x-3
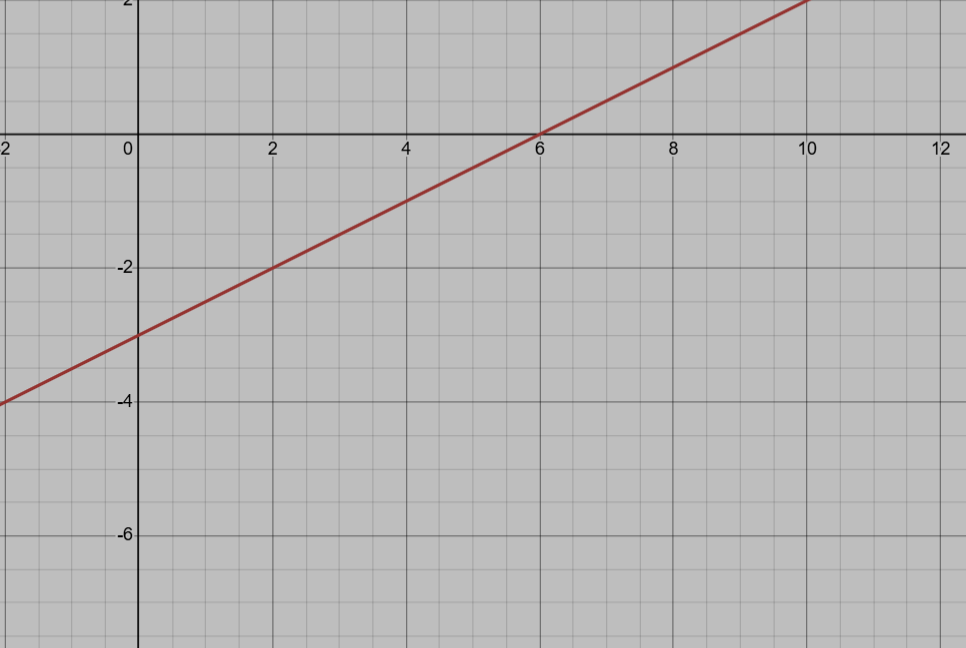
What is the difference between the SLOPES of parallel and perpendicular lines?
Parallel lines have the same slope.
Perpendicular lines have opposite reciprocals.
Solve the system of equations shown below:
y=2x+3
x+4y=39
(3, 9)
Solve for variable x below:
7x + 4 = 7x - 9
No solution is possible
A school club charges $12 per ticket and already has $48 saved.
How much money will the club have after selling 20 tickets?
$288
Find the x and y-intercepts for the standard form equation below:
3x + 9y = 27
(9,0) and (3,0)

Write an equation in slope-intercept form that passes through the point (6,-2) but is parallel to the line below:
y=2/3x+4
y=2/3x-6
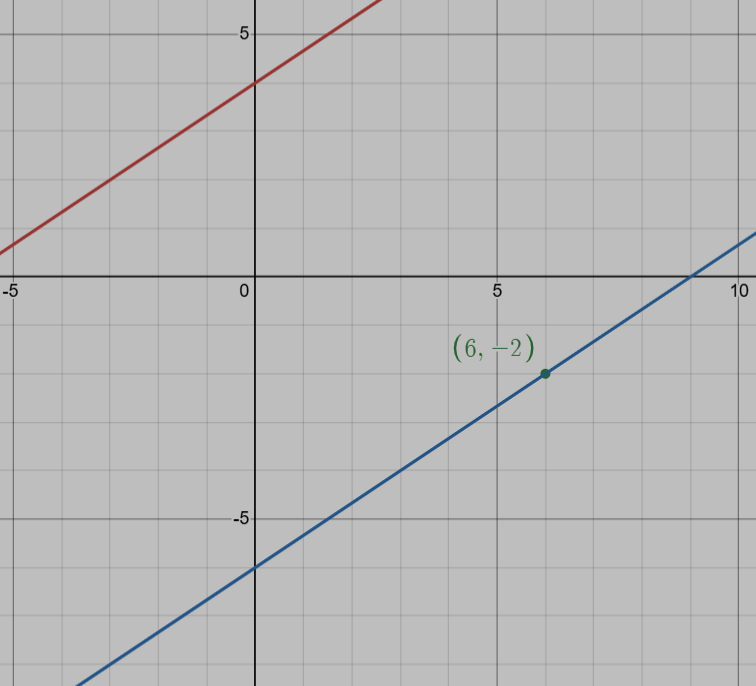
Name a coordinate point that is a solution to the system of inequalities shown below:
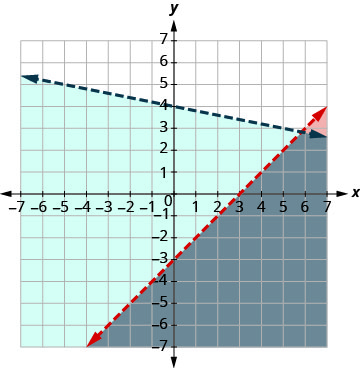
Anything in the dark blue region!
Solve for the variable x below:
5(x - 2) = 5x - 10
Infinite solutions are possible
Solve for the variable x below:
-4x + 7 ≤ 2x - 5
x ≥ 2
Graph the equation on the coordinate plane:
y=-1/3x+2
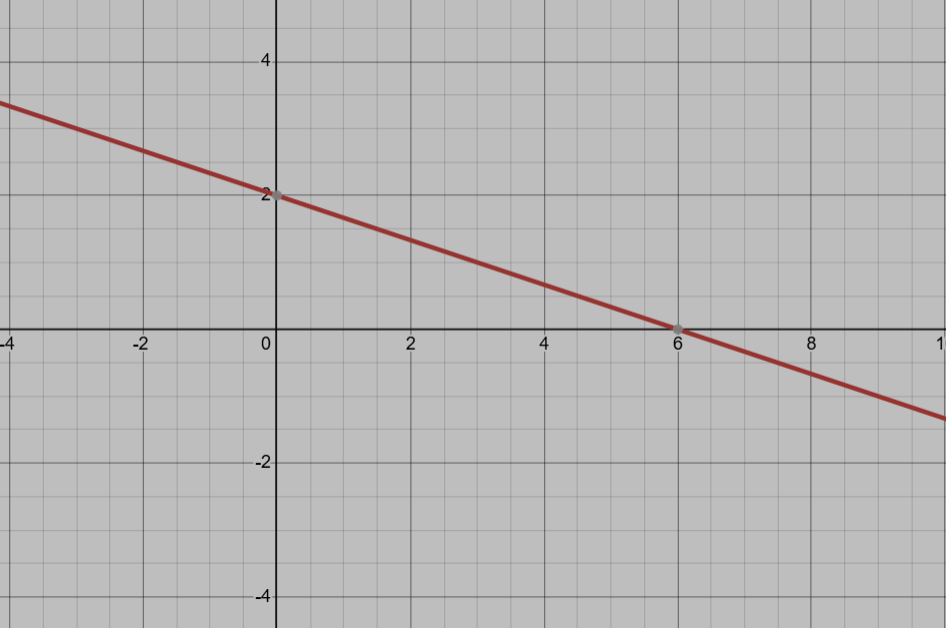
Write an equation in slope-intercept form that passes through the point (3,-2) but is perpendicular to the line below:
y=1/2x-7
y=-2x+5
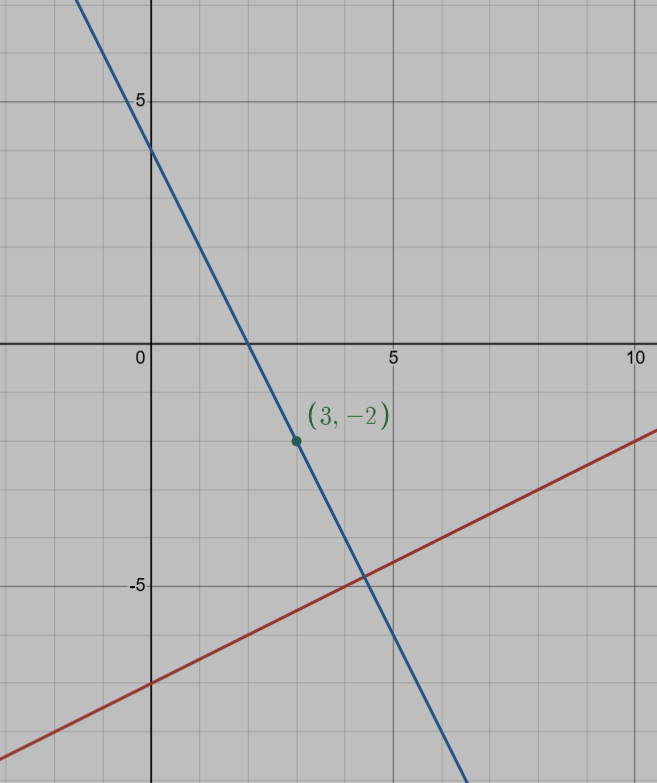
At the concession stand, you buy burgers and bags of chips, a mixture of 12 items. Burgers cost $4 and chips cost $2, and your bill is $30.
Determine how many burgers and bags of chips you bought.
3 burgers and 9 chips
Setup:
x+y=12
4x+2y=30
Solve for the variable x:
3(2x + 5) - 4x = 22
x= 3.5 or 7/2
A school club charges $12 per ticket and already has $48 saved.
How many tickets must be sold to earn $300 total?
21 tickets
Find the x and y-intercepts for the standard form equation below:
4x - 2y = 20
(5,0) and (0,-10)

Write an equation in slope-intercept form that passes through the point (5,-4) but is parallel to the line below:
y=-2x+1
y=-2x+6

Write an inequality for the graph shown:

y≥-3x+3
Solve for the variable x below:
2x+4y=6z
x=-2y+3z
Solve the compound inequality below:
2x - 1 > 7 or -3x + 2 > 11
x > 4 or x < -3
Write and graph an equation in slope-intercept form that passes through the points (0, 8) and (-3, 2)
y=2x+8

Write an equation in slope-intercept form that passes through the point (12, -2) but is perpendicular to the line below:
y=3x-7
y=-1/3x+2

Say that Mario and Yoshi have a combined age of 46. Yoshi is 13 years older than twice Mario's age.
Determine Mario and Yoshi's ages.
Mario is 11
Yoshi is 35
Setup:
x+y=46
y=2x+13