Properties of Integrals
Fundamental Theorem of Calculus, Part 2
Fundamental Theorem of Calculus, Part 1
Basic Integrals 1
Basic Integrals 2
Integrals w/ Geometry
Riemann Sums
100
int [f(x)+g(x)]dx
intf(x)dx + intg(x)dx
100
d/dxint_0^x(t+1)dt
x+1
100
int_0^2 3x^2dx
8
100
int(x^3-2x^2+x+3)dx
x^4/4-(2x^3)/3+x^2/2+(3x)/1+C
100
int-9dx
-9x+C
100
Graphically represent the following:
int_-3^2(2x+1)dx
100
This is the approximate area of the function's curve in relation to the x-axis using a Right-Hand Riemann Sum with 4 subintervals on the closed interval [-2, 2].
f(x)=3x^2+1
What is 22 units?
200
int_1^3f(x)=3, int_3^1f(x)=?
-3
200
d/dxint_pi^x(tsint)/(t-1)dt
(xsinx)/(x-1)
200
int_-1^1 e^xdx
e^1-e^-1
200
int(sqrt(x)+x^(-2)+root(3)x^4)dx
2/3x^(3/2)+x^-1/-1+3/7x^(7/3)+C
200
int((4x^2-x)/x)dx=this
What is
2x^2-x+C?
200
This is the exact area of the function's curve in relation to the x-axis on the closed interval [-2, 4].
What is 7 Units?
200
Approximate the are between g(x) and the x-axis from x=0 to x=1.5 using a left Riemann sum with 3 equal subdivisions.
6 units
300
int_a^af(x)dx
0
300
d/dxint_x^-1ln(t^2-1)dt
-ln(x^2-1)
300
int_(-pi/2)^(pi/2)cosxdx
2
300
int cscxcotxdx
-cscx+C
300
int((sqrt(x))^3+2root4x-1/(x^2))dx
What is
2/5x^(5/2)+8/5x^(5/4)+1/x+C?
300
This is the exact area of the function's curve in relation to the x-axis on the closed interval [0, 12].
What is
-15/2+2\pi
Units?
300
This is the approximate area of the function's curve in relation to the x-axis using a Midpoint Riemann Sum with 3 subintervals on the closed interval [1, 10].
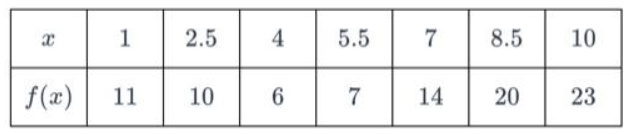
What is 91 Units?
400
int_1^3f(x)=4 and int_3^6f(x)=12,
int_1^6f(x)=?
16
400
d/dxint_0^(2x^2+x)t(t-2)^2dt
(2x^2+x)(2x^2+x-2)^2(4x+1)
400
int_1^4 sqrtx - 2x \ dx
-10.33
400
int 4/sqrt(1-x^2)dx
4sin^-1x+C
400
int (x-2)(3x^2-7x)dx
What is
3/4x^4-13/3x^3+7x^2+C?
400
Evaluate the Integral
int_-1^1 1-|x| dx
1
400
This is the approximate area of the function's curve in relation to the x-axis with appropriate units using a Trapezoidal Sum with 4 subintervals on the closed interval [0, 4].
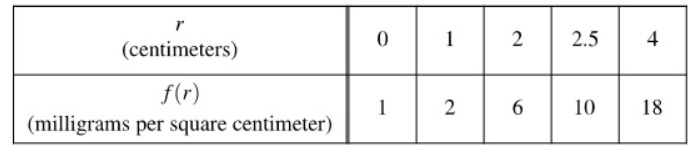
What is 30.5 milligrams per centimeter?
500
int_2^9f(x)=20 and int_4^9f(x)=11,
int_2^4f(x)=?
9
500
F(x)=∫_(x^3)^(x^4) 1/(1+t^2) dt
(4x^3)/(1+x^8)-(3x^2)/(1+x^6)
500
int_1^2(1/x^2+1/x+1)dx
3/2+ln2
500
17
500
int(3e^x+1/x-1/x^2)dx
3e^x+ln|x|+1/x+C
500
Evaluate the Integral (hint: graph and use geometric formula)
int_-3^3 \sqrt(9-x^2)
(9\pi)/2
500
What is the trapezoidal sum approximation for
int_4^14f(x)dx
using three subintervals as indicated by the table
189/2 or 94.5