Relations and Functions
Linear Functions
Transforming Linear Functions
Arithmetic Sequences
100
What is the domain? What is the range? Is the relation a function?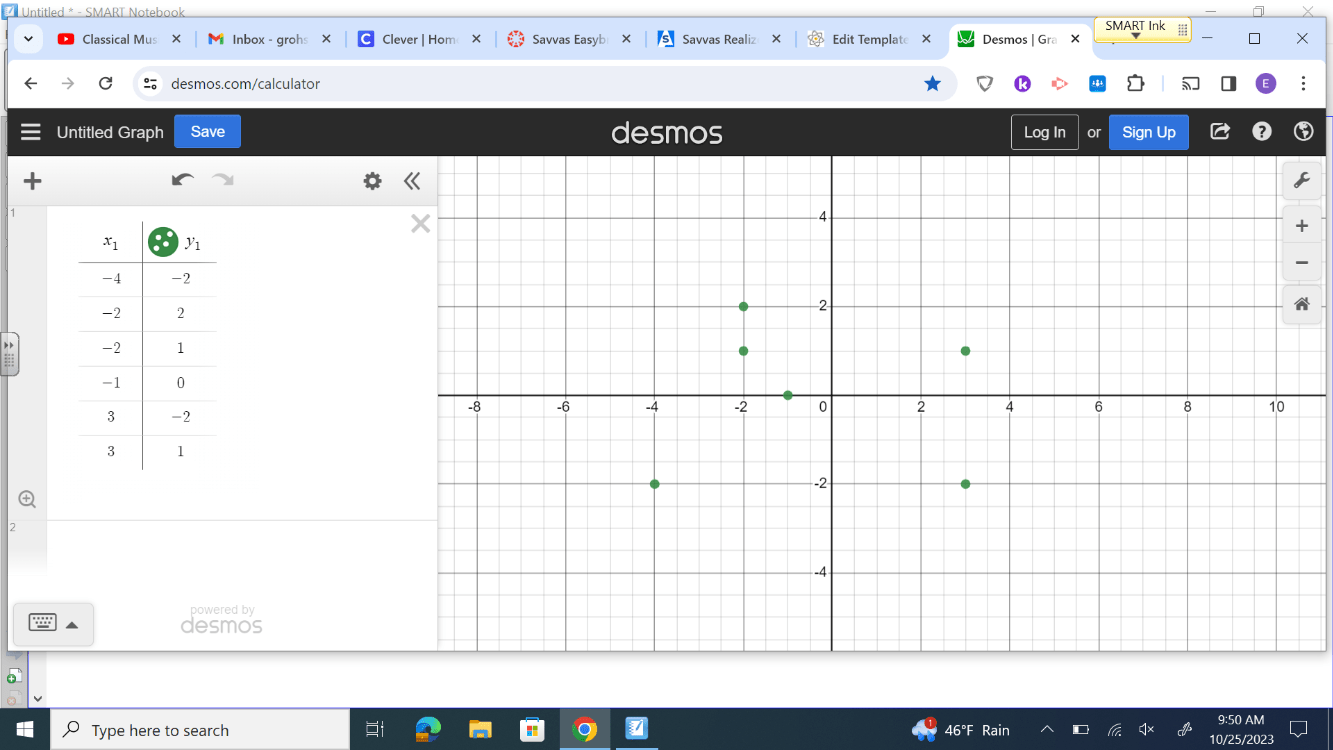
D: {-4,-2,-1,3}
R: {-2,0,1,2}
Not a function
100
Find the value of f(3) for the function f(x)=−3(x+2)
-15
100
Given f(x) = 4x + 1, describe how the graph of g compares with the graph of f.
g(x) = 4(x + 3) + 1
Horizontal shift 3 units left.
100
Write a recursive formula for the sequence
81,85,89,93,97,...
an=an-1+4 a1=81
200
Is this relation a function? Explain why or why not.
Yes. There is only one output per input. Many to one.
200
Sketch the graph of the function h(x) = 3 − x
200
Given f(x) = 4x + 1, describe how the graph of g compares with the graph of f.
g(x) = (4x + 1) + 3
Vertical shift up 3.
200
Write an explicit formula for the sequence
81,85,89,93,97,...
an=81+(n-1)4
or
an=77+4n
300
Is this relation a function? Explain why or why not.
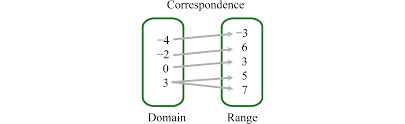
No. It is one to many. The input of 3 relates to two different outputs -- 7 and 5.
300
x 0 1 2 3 4
f(x) 180 174 168 162 156
What is the function of these values?
f(x)=180-6x
300
Given f(x) = x + 2, describe how setting k = 4 affects the slope and y-intercept of the graph of g compared to the graph of f.
g(x) = 4(x + 2)
The graph gets steeper by a factor of 4. The y-intercept goes from 2 to 8.
300
Write an explicit formula for the recursive formula
an=an-1+15 a1=8
an=15n-7
400
Cameron earns an hourly wage at his job. He makes a table of the number of hours he works each week and the amount of money he earns.
Which units should be put on the x-axis? Identify any constraints on the domain. In other words, what values of x would not make sense?
Hours work on the x-axis. X should not be negative.
400
Hours 0.5 1 1.5 2 2.5
Labor $60 $90 $120 $150 $180
Write a function for the table of values.
f(x)=60x+30
400
Let
f(x)=1/2x-3
Suppose you subtract 6 from the input of f to create a new function g, and then multiply the input of function g by 4 to create a function h. What equation represents h?
h(x)=2x-6
400
After the first raffle drawing, 497 tickets remain. After second raffle drawing, 494 tickets remain. Assuming that the pattern continues, write an explicit formula for an arithmetic sequence to represent the number of raffle tickets that remain after each drawing.
an=500-3n
500
Analyze the situation. Identify a reasonable domain and range for the situation.
The revenue earned from a sporting event can be determined by the ticket price, $125 each.
The domain is:
Domain is all whole numbers.
Range is all whole number multiples of 125
500
Katrina buys a 64-ft roll of fencing to make a rectangular play area for her dogs. Use 2(l + w) = 64 to write a function for the length, given the width. Graph the function. What is a reasonable domain for the situation? Explain.
l=32-w
Domain must be greater than 0 and less than 32, otherwise the fence would have no length or width.
500
Given f(x) = 3x + 5, describe how the graph of g compares with the graph of f.
g(x) = 3(0.1x) + 5
The slope goes from 3 to 0.3
A vertical compression by a factor of 0.1
500
How many tickets remain in the bag after the seventh raffle?
479