Integration Methods
Series
Parametric Equations
Polar Equations
100
\int 1/(x(x+1)) dx
ln(x)-ln(x+1)+C
100
1+1/3+1/9+1/27+...
3/2
100
What is a parametric representation for
x^2+y^2=1
(x(t),y(t))=(cos(t),sin(t))
100
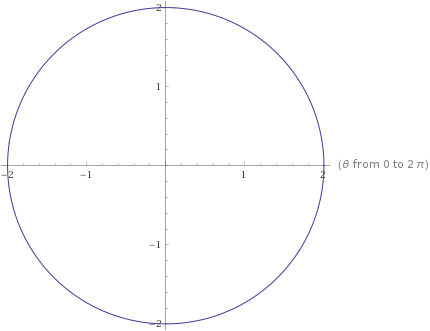
Graph
r=2, 0\leq\theta\leq 2\pi
200
\int_0^1 xe^x dx
1
200
Does the series converge or diverge?
\sum_{n=1}^\infty 2/n^2
Converges.
200
Find the Cartesian equation for
(x(t),y(t))=(t+1,2t-1)
y=2x-3
200
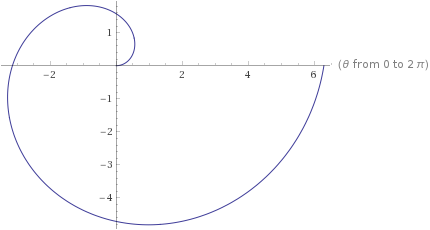
Graph
r=\theta, 0\leq\theta\leq2\pi
300
\int 1/\sqrt{1-x^2} dx
sin^{-1}(x)+C
300
Does the series converge or diverge?
\sum_{n=1}^\infty 1/(2^n-1)
Converges.
300
Calculate dy/dx for
(x(t),y(t))=(sin^2t,cost)
-1/2 sec(t)
300
Convert the polar coordinates in Cartesian:
(2,\pi/3)
(1,\sqrt{3})
400
\int x/\sqrt{x^2+16} dx
\sqrt{x^2+16}+C
400
Does the series converge or diverge?
\sum_{n=1}^\infty (n^2+3n-1)/(1-2n^2)
Diverges.
400
Set up the integral (don't solve) for the arc length of
(x,y)=(2cos t,sin t), 0\leq t\leq 2pi
\int \sqrt{4sin^2t+cos^2t} dt
400
Find dy/dx of
r=\theta
dy/dx=(sin(\theta)+\theta cos(\theta))/(cos(\theta)-\theta sin(\theta))
500
\int_{-2}^2 1/x^2 dx
Not defined.
500
What is the interval of convergence for the series?
\sum_{n=1}^\infty (x/3-2)^n
(3,9)
500
Set up the integral (do not solve) for area enclosed by
(x,y)=(2cos t,sin t), 0\leq t\leq 2pi
-2\int_0^{2\pi} sin^2(t) dt
500
Find arc length of
r=sin(\theta), 0\leq \theta\leq \pi
pi