Going from the specific cases to a general conclusion.
What is inductive reasoning?
If p is True, what is NOT p?
False
Complete the following table with the conjunction condition. (What? You were expecting an easy question here?!)
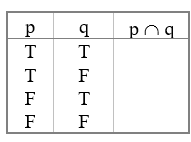
TFFF
The conjunction is the AND condition. Both (or all) must be true in order th get a true conclusion.
When comparing two propositions it is true when both propositions have the same truth value (T-T or F-F), and false when their truth values differ (F-T or T-F).
What is the Biconditional (IFF)?
"Boys have short hair."
Turn this into a proper conditional statement. Remember, it matters not whether the statement is always true, sometimes true or never true.
IF you are a boy,
THEN you have shorty hair.
Going from a general proposition to a specific conclusion.
What is deductive reasoning?
What does this symbol represent? 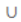
disjunction which says "Or"
Two propositions are ________ if and only if they have identical truth values in a truth table.
What is Logically Equivalent?
I am the symbol for the biconditional.
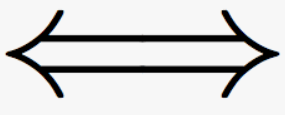 ↔
↔
"IF you are a boy, THEN you have short hair."
State the converse.
Remember, it matters not whether the statement is always true, sometimes true or never true.
"IF you have short hair THEN you are a boy."
True-false: Inductive reasoning cannot be proven to be false.
false - just find a counter-example
What does this symbol represent?
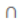
What is "conjunction" which says "and"
Complete the truth table for disjunction. (4 output values)
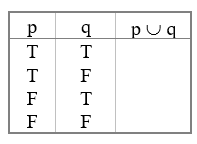
What is TTTF
The disjunction refers to the OR condition. If either one is true (or both), then the conclusion is true.
In a conditional if P then Q, the _________ is the proposition represented by the P.
What is the hypothesis?
If you wish to prove an inductive statement to be false, then you will need a __________________ to show that it is not valid.
What are Contradiction? Also, what is a counter example?
In order to show that an inductive proposition is false, how many counter examples do we need?
ONE counter example
What do i mean by "disjunction"?
Or
Complete the last two columns of the following truth table:
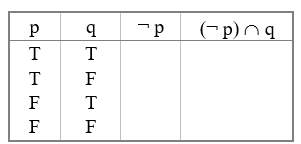
Thought that this would be easier than the 500 question? OOPS
In a conditional if P then Q, the ____________ is the proposition represented by the Q.
What is the conclusion?
"IF you are a boy, THEN you have short hair."
State the inverse.
Remember, it matters not whether the statement is always true, sometimes true or never true.
"If you are not a boy, then you do not have short hair."
What do we call those tables organized to show the possible results of our logic?
What is truth tables?
p = T q = F If I am "and," what is the result of p and q?
False (F)
The truth table for the biconditional. IFF 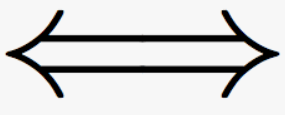
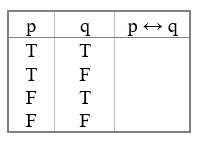
What is TFFT?
(True when both agree ONLY)
Which of the following will always be true, assuming that the original statement is true?
inverse
converse
contrapositive
What is the contrapositive?
"IF you are a boy, THEN you have short hair."
State the contrapositive.
Remember, it matters not whether the statement is always true, sometimes true or never true.
If you do not have short hair, then you are not a boy."