x and y tables
Level 4 Questions
Solving Linear Inverses
Solving Square Root Inverses
100
Find the inverse: x | y ------ 2 | 3 5 | 6 2 | 4
What is x | y ----- 3 | 2 6 | 5 4 | 2
100
Verify if
f(x)=(x+4)/2
and
g(x)=2(x-4)
are inverses or not.
Put one function in for "x" into the other equation, so f(g(x)), which is
((2x+4) + 4)/2
=(2x+8)/2
=(2x)/2 + 8/2
=x+4 NO!!
100
Solve for the inverse of y = x - 3
What is f^-1(x) = x + 3
100
Solve for the inverse of y = x²
What is f^-1(x) = ±√(x)
200
Find the inverse of:
x | y
----------
-2 | 10
4 | 6
8 | 0
What is
x | y
----------
10 | -2
6 | 4
0 | 8
200
If
f(x)=-3(x+2)^2 {x>=-2}
, then find
f^-1(-27)
.
You can do it 2 different ways:
1.
f^-1 (-27)
is the input for the INVERSE, so it's the output for the original, so
-27=-3(x+2)^2
Then you can undo both sides, solve it and get
x=1.
2. You can find the inverse, then put in -27 for x.
f^-1(x)=sqrt(x/-3)-2
f^-1(27)=sqrt(-27/-3)-2
=sqrt(9)-2
=3-2=1
200
Solve for the inverse of y = 8x
What is f^-1(x) = x/8
200
Solve for the inverse of y = x² + 2
What is f^-1(x) = ±√(x - 2)
300
Make an x- and y- table of at least 3 points for y = x - 2.
What is
x | y
----------
-2 | 0
-1 | -3
0 | -2
1 | -1
2 | -2
300
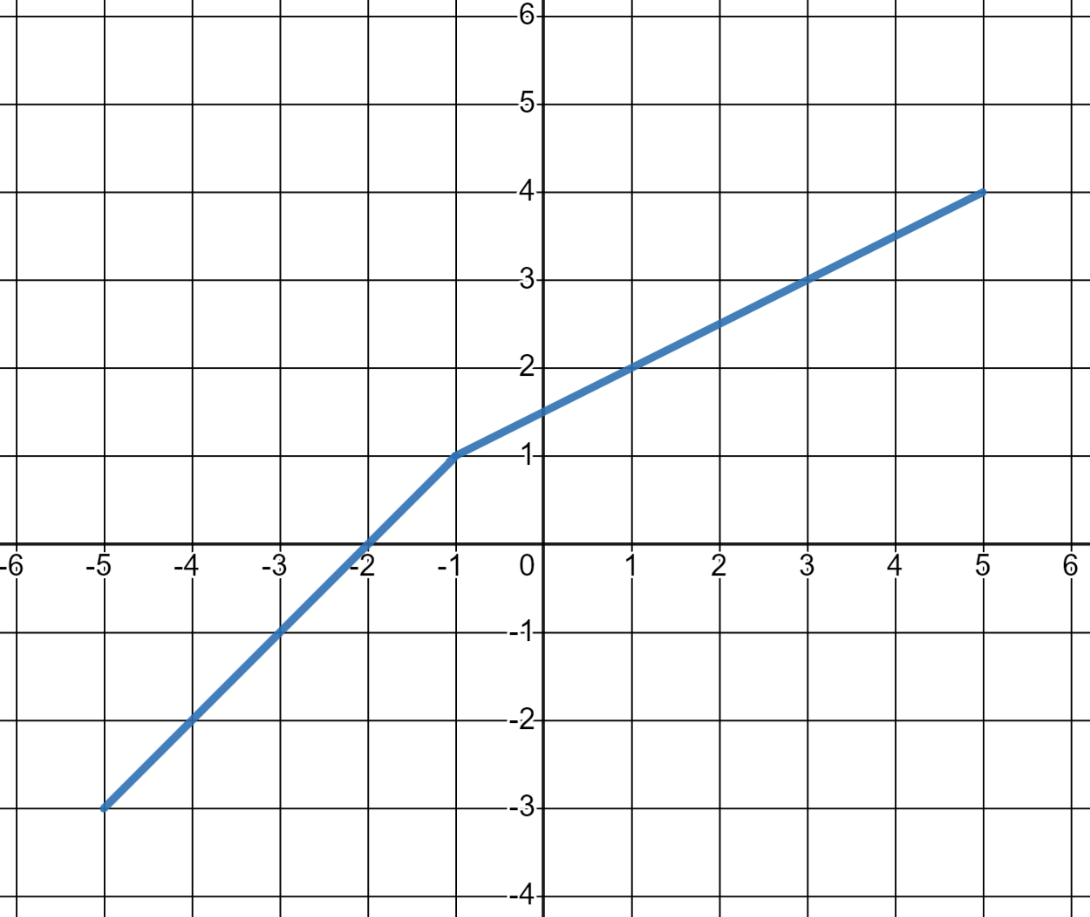If the graph below is
f(x)
, find
f^-1(-2)
.
The input for the inverse is the OUTPUT for the original equation. So go to where the output is -2. What is the input?
-4.
300
Solve for the inverse of y = 3x + 2
What is f^-1(x) = (x - 2) / 3
300
Solve for the inverse of y = -2x² - 4.
What is f^-1(x) = ±√( (x + 4) / -2)
400
Make an x- and y-chart with at least 3 points for y = 2x² - 1 and find its inverse x- and y-chart.
What is
x | y x | y
-------- ---------
-2 | 7 7 | -2
-1 | 1 1 | -1
0 | -1 and what is -1 | 0
1 | 1 1 | 1
2 | 7 7 | 2
400
Verify that
f(x)=2x-1 and g(x)=(x+1)/2
are inverses.
Plug one function in for "x" in the other equation,
2((x+1)/2)-1=(x+1)-1=x
so YES!
400
Solve for the inverse of y = 2x - (4x + 1)
What is f^-1(x) = (x + 1) / -2
400
Solve for the inverse of y = 2(x² + 1)
What is f^-1(x) = ±√((x - 2) / 2)